Quasi-standardabweichung

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was eine Quasi-Standardabweichung in der Statistik ist und wie sie berechnet wird. So finden Sie die Quasi-Standardabweichungsformel, eine gelöste Übung und zusätzlich einen Online-Rechner zur Berechnung der Quasi-Standardabweichung eines beliebigen Datensatzes.

Was ist eine Quasi-Standardabweichung?

In der Statistik ist die Quasi-Standardabweichung ein Maß für die Streuung, das die Variabilität der Stichprobe angibt. Konkret ist die Quasi-Standardabweichung gleich der Quadratwurzel der Summe der Quadrate der Abweichungen dividiert durch die Gesamtzahl der Datenpunkte minus eins.

Das Symbol für die Quasi-Standardabweichung ist σ _n-1 os _n-1 .

Die Quasi-Standardabweichung kann auch als Quasi-Standardabweichung bezeichnet werden und wird manchmal auch als Stichprobenstandardabweichung bezeichnet, da sie normalerweise anhand von Werten aus einer statistischen Stichprobe berechnet wird. Im Folgenden gehen wir detailliert auf den Unterschied zwischen Quasi-Standardabweichung und Standardabweichung ein.

Quasi-Standardabweichungsformel

Die Quasi-Standardabweichung ist gleich der Quadratwurzel der Summe der Quadrate der Abweichungen der Datenreihe dividiert durch die Gesamtzahl der Beobachtungen minus eins. Daher lautet die Formel zur Berechnung der Quasi-Standardabweichung :

Gold:

$\sigma_{n-1}$

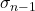
Dies ist die Quasi-Standardabweichung.
$x_i$

ist der Datenwert

$i$

.
$n$

ist die Gesamtzahl der Daten.
$\overline{x}$

ist der Mittelwert des Datensatzes.

👉 Mit dem Rechner unten können Sie die Quasi-Standardabweichung für jeden Datensatz berechnen.

Beispiel für die Berechnung der Quasi-Standardabweichung

In Anbetracht der Definition der Quasi-Standardabweichung sehen Sie unten ein einfaches Beispiel für die Berechnung der Quasi-Standardabweichung eines Datensatzes.

Das Budget eines Unternehmens für seine Forschungs- und Entwicklungsabteilung ist sehr volatil, da es vom wirtschaftlichen Gewinn abhängt, den das Unternehmen im Vorjahr erzielt hat. Somit betrug das Budget für diesen Abschnitt in den letzten fünf Jahren: 3, 6, 2, 9, 4 Millionen Euro. Berechnen Sie die Quasi-Standardabweichung dieser Datenreihe.

Um die Quasi-Standardabweichung zu bestimmen, müssen wir zunächst das arithmetische Mittel der Stichprobe berechnen. Dazu addieren wir alle Daten und dividieren durch die Gesamtzahl der Beobachtungen, also fünf:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Als nächstes wenden wir die Quasi-Standardabweichungsformel an:

$\displaystyle\sigma_{n-1}=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}}$

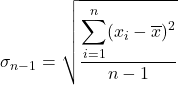
Wir setzen die Daten in die Formel ein:

$\displaystyle \sigma_{n-1}=\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5-1}}$

Und schließlich berechnen wir die Quasi-Standardabweichung:

$\begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}$

Kurz gesagt beträgt die Quasi-Standardabweichung der Datenstichprobe 2,77 Millionen.

➤ Siehe: Quasivarianz

Quasi-Standardabweichungsrechner

Geben Sie einen statistischen Datensatz in den Online-Rechner unten ein, um seine Quasi-Standardabweichung zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Quasi-Standardabweichung und Standardabweichung

Abschließend werden wir sehen, was der Unterschied zwischen Quasi-Standardabweichung und Standardabweichung ist, da es sich um zwei verschiedene statistische Maße handelt, die einen sehr ähnlichen Namen haben und auf sehr ähnliche Weise berechnet werden.

Die Differenz zwischen der Quasi-Standardabweichung und der Standardabweichung ist der Nenner der Formel. Um die Quasi-Standardabweichung zu berechnen, dividieren Sie durch n-1, die Standardabweichung wird jedoch durch Division durch n berechnet.

Daher hängen Quasi-Standardabweichung und Standardabweichung mathematisch zusammen, da die Quasi-Standardabweichung der Standardabweichung multipliziert mit der Quadratwurzel von n (Gesamtzahl der Datenpunkte) über n-1 entspricht.

$\displaystyle\sigma_{n-1}=\sqrt{\frac{n}{n-1}}\cdot \sigma$

Aus der vorherigen Gleichung können wir ableiten, dass für denselben Datensatz der Wert der Quasi-Standardabweichung immer größer sein wird als der Wert der Standardabweichung.

Darüber hinaus wird die Quasi-Standardabweichungsformel häufig zur Berechnung der Standardabweichung einer Stichprobe verwendet, da sie Verzerrungen eliminiert. Die Quasistandardabweichung ist daher ein guter Schätzer für die Standardabweichung der Grundgesamtheit. Aus diesem Grund wird bei statistischen Schlussfolgerungen aus einer Stichprobe häufig davon ausgegangen, dass die Standardabweichung berechnet wird, während in Wirklichkeit die Quasi-Standardabweichung berechnet wird.

➤ Siehe: Eigenschaften der Standardabweichung

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen