Quasivarianz

In diesem Artikel wird erklärt, was Quasivarianz in der Statistik ist. So erfahren Sie, wie man die Quasivarianz berechnet, eine gelöste Aufgabe und was die Unterschiede zwischen der Quasivarianz und der Varianz sind. Darüber hinaus können Sie die Quasivarianz jedes Datensatzes mit einem Online-Rechner berechnen.

Was ist Quasivarianz?

In der Statistik ist Quasivarianz ein Maß für die Streuung, das die Variabilität einer Stichprobe angibt. Genauer gesagt ist die Quasivarianz gleich der Summe der Quadrate der Abweichungen geteilt durch die Gesamtzahl der Beobachtungen minus eins.

Das Symbol für Quasivarianz ist

entweder

. Manchmal wird das Symbol zwar auch verwendet

um die Quasivarianz darzustellen.

Quasivarianz wird verwendet, um die Streuung einer Stichprobe unter Vermeidung von Verzerrungen zu bestimmen, weshalb sie oft als erwartungstreue Varianz bezeichnet wird. Die Quasivarianz ist daher ein guter Schätzer für die Populationsvarianz. Tatsächlich wird bei der Berechnung der Stichprobenvarianz häufig die Quasi-Varianzformel anstelle der Varianzformel verwendet. Im Folgenden gehen wir detailliert auf den Unterschied zwischen diesen beiden statistischen Maßen ein.

Quasivarianzformel

Um die Quasivarianz zu berechnen, muss man die Summe der Quadrate der Differenzen zwischen den Werten und dem Mittelwert des Datensatzes ermitteln und diese später durch die Gesamtzahl der Daten minus eins dividieren.

Die Formel zur Berechnung der Quasivarianz lautet also wie folgt:

Gold:

• 

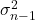
  ist die Quasivarianz.

• 

  ist der Datenwert

  

  .

• 

  ist die Gesamtzahl der Daten.

• 

  ist der Mittelwert des Datensatzes.

👉 Mit dem Rechner unten können Sie die Quasivarianz eines beliebigen Datensatzes berechnen.

Sie fragen sich vielleicht, warum es durch n-1 und nicht durch n geteilt wird? Nun, es geht darum, die Verzerrung zu beseitigen. Auf diese Weise erhalten wir einen unvoreingenommenen Schätzer. Genau aus diesem Grund ist die Quasivarianz ein guter Schätzer für die Populationsvarianz.

Beispiel einer Quasivarianzberechnung

Nachdem wir nun die Definition der Quasivarianz kennen, lösen wir ein einfaches Beispiel, damit Sie sehen können, wie die Quasivarianz einer Datenreihe berechnet wird.

• Von einem multinationalen Unternehmen kennen wir die wirtschaftlichen Ergebnisse, die es in den letzten fünf Jahren erzielt hat. In den meisten Fällen erzielte es Gewinne, in einem Jahr verzeichnete es jedoch erhebliche Verluste: 11,5, 2, -9, 7 Millionen Euro. Berechnen Sie die Quasivarianz dieses Datensatzes.

Um die Quasivarianz eines Datensatzes zu ermitteln, müssen wir zunächst sein arithmetisches Mittel berechnen:

Und sobald wir den Durchschnittswert der Daten kennen, wenden wir die Quasivarianzformel an:

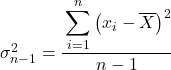
Daher setzen wir die in der Übungsanweisung bereitgestellten Daten in die Formel ein:

Abschließend genügt es, die Operationen zur Berechnung der Quasivarianz zu lösen:

Beachten Sie, dass die Einheiten der Quasivarianz dieselben Einheiten wie die Einheiten der statistischen Daten sind, jedoch quadriert, sodass die Quasivarianz dieses Datensatzes 57,2 Millionen ² beträgt.

Quasivarianzrechner

Geben Sie einen statistischen Datensatz in den folgenden Rechner ein, um seine Quasivarianz zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Varianz und Quasivarianz

Schließlich werden wir den Unterschied zwischen Quasivarianz und Varianz sehen, denn trotz ihrer Namensähnlichkeit werden sie auch sehr ähnlich berechnet.

Der Unterschied zwischen der Quasivarianz und der Varianz ist der Nenner der Formel. Um die Quasivarianz zu berechnen, müssen Sie durch n-1 dividieren. Die Varianz wird jedoch durch Division durch n berechnet.

Somit hängen Quasivarianz und Varianz mathematisch zusammen, da Quasivarianz der Varianz multipliziert mit n (der Gesamtzahl der Datenpunkte) und dividiert durch n-1 entspricht.

Daher ist für denselben Datensatz der Quasivarianzwert immer größer als der Varianzwert.