So führen sie einen kolmogorov-smirnov-test in excel durch

Mit dem Kolmogorov-Smirnov-Test wird ermittelt, ob eine Stichprobe normalverteilt ist oder nicht.

Dieser Test wird häufig verwendet, da viele statistische Tests und Verfahren davon ausgehen , dass die Daten normalverteilt sind.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie ein Kolmogorov-Smirnov-Test an einem Beispieldatensatz in Excel durchgeführt wird.

Schritt 1: Geben Sie die Daten ein

Beginnen wir mit der Eingabe von Werten aus einem Datensatz mit einer Stichprobengröße von n = 20:

Schritt 2: Berechnen Sie die tatsächlichen und erwarteten Werte aus der Normalverteilung

Als nächstes berechnen wir die tatsächlichen Werte im Vergleich zu den erwarteten Werten der Normalverteilung:

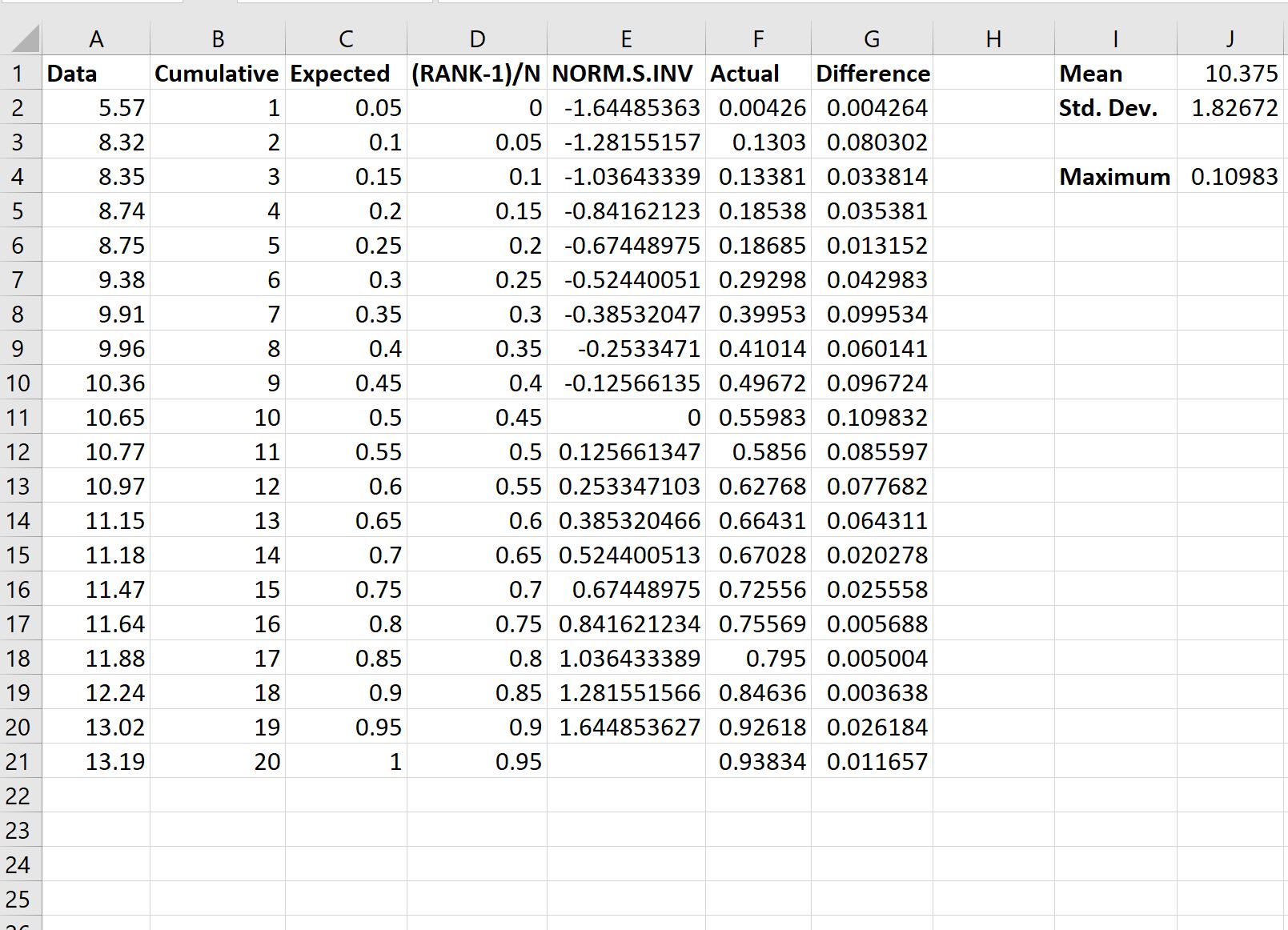
Hier ist die Formel, die wir in verschiedenen Zellen verwendet haben:

• B2 : =LINE() – 1
• C2 : = B2 /COUNT( $A$2:$A$21 )
• D2 : =( B2 -1)/COUNT( $A$2:$A$21 )
• E2 : =IF( C2 <1, NORM.S.INV( C2 ),“)
• F2 : =NORM.DIST( A2 , $J$1 , $J$2 , TRUE)
• G2 : =ABS( F2 – D2 )
• D1 : =DURCHSCHNITT( A2:A21 )
• J2 : =ETDEV.S( A2:A21 )
• J4 : =MAX( G2:G21 )

Schritt 3: Interpretieren Sie die Ergebnisse

Ein Kolmogorov-Smirnov-Test verwendet die folgenden Null- und Alternativhypothesen:

• H ₀ : Daten sind normalverteilt.
• H _A : Die Daten sind nicht normalverteilt.

Um zu bestimmen, ob wir die Nullhypothese ablehnen sollten oder nicht, müssen wir uns auf den Maximalwert in der Ausgabe beziehen, der sich als 0,10983 herausstellt.

Dies stellt die maximale absolute Differenz zwischen den tatsächlichen Werten unserer Stichprobe und den erwarteten Werten einer Normalverteilung dar.

Um zu bestimmen, ob dieser Maximalwert statistisch signifikant ist, muss man sich auf eine Kolmogorov-Smirnov-Tabelle kritischer Werte beziehen und die Zahl finden, die n = 20 und α = 0,05 entspricht.

Der kritische Wert liegt bei 0,190 .

Da unser Maximalwert nicht größer als dieser kritische Wert ist, können wir die Nullhypothese nicht ablehnen.

Das bedeutet, dass wir davon ausgehen können, dass unsere Beispieldaten normalverteilt sind.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige statistische Tests in Excel durchführen:

So führen Sie einen Korrelationstest in Excel durch
So führen Sie einen Durbin-Watson-Test in Excel durch
So führen Sie einen Jarque-Bera-Test in Excel durch
So führen Sie den Levene-Test in Excel durch