Regression durch den ursprung: definition & beispiel

Die einfache lineare Regression ist eine Methode, mit der die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen quantifiziert werden kann.

Ein einfaches lineares Regressionsmodell hat die folgende Form:

y = β ₀ + β ₁ x

Gold:

• y : Der Wert der Antwortvariablen
• β ₀ : Der Wert der Antwortvariablen, wenn x = 0 (als „Intercept“-Term bezeichnet)
• β ₁ : Der durchschnittliche Anstieg der Antwortvariablen, der mit einem Anstieg von x um eine Einheit verbunden ist
• x : Der Wert der Vorhersagevariablen

Eine modifizierte Version dieses Modells ist als Regression durch den Ursprung bekannt und erzwingt, dass y gleich 0 ist, wenn x gleich 0 ist.

Diese Art von Modell hat die folgende Form:

y = _β1x

Beachten Sie, dass der Intercept-Term vollständig aus dem Modell entfernt wurde.

Dieses Modell wird manchmal verwendet, wenn Forscher wissen, dass die Antwortvariable Null sein muss, wenn die Prädiktorvariable Null ist.

In der realen Welt wird dieser Modelltyp am häufigsten in forstwirtschaftlichen oder ökologischen Studien verwendet.

Beispielsweise können Forscher den Baumumfang nutzen, um die Baumhöhe vorherzusagen. Wenn ein gegebener Baum einen Umfang von Null hat, muss er auch eine Höhe von Null haben.

Wenn man also ein Regressionsmodell an diese Daten anpasst, wäre es nicht sinnvoll, wenn der ursprüngliche Term ungleich Null wäre.

Das folgende Beispiel zeigt den Unterschied zwischen der Anpassung eines gewöhnlichen einfachen linearen Regressionsmodells und eines Modells, das die Regression über den Ursprung implementiert.

Beispiel: Regression durch den Ursprung

Angenommen, ein Biologe möchte ein Regressionsmodell mithilfe des Baumumfangs anpassen, um die Baumhöhe vorherzusagen. Sie geht los und sammelt die folgenden Maße für eine Stichprobe von 15 Bäumen:

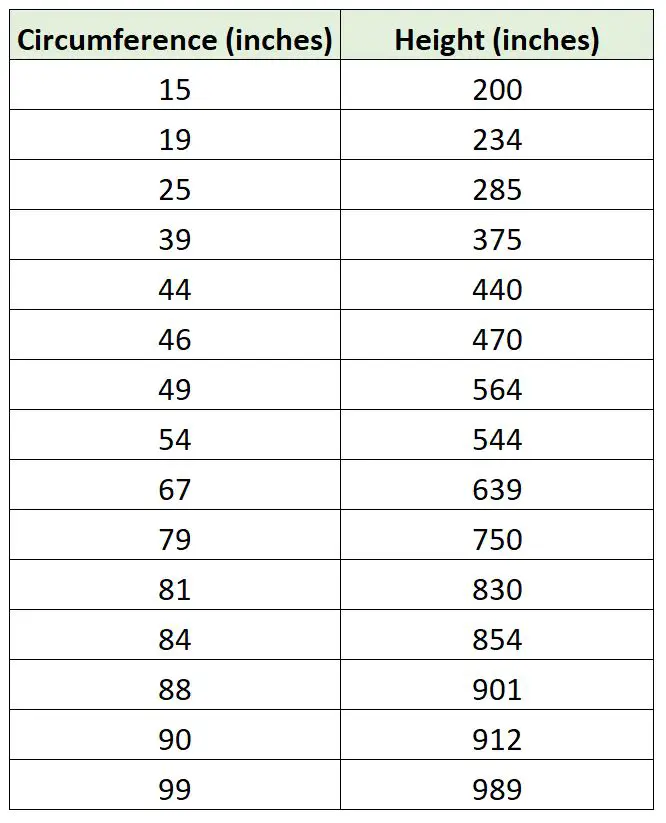
Wir können den folgenden Code in R verwenden, um ein einfaches lineares Regressionsmodell an ein Regressionsmodell anzupassen, das keine Achsenabschnitte verwendet, und die beiden Regressionslinien zu zeichnen:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

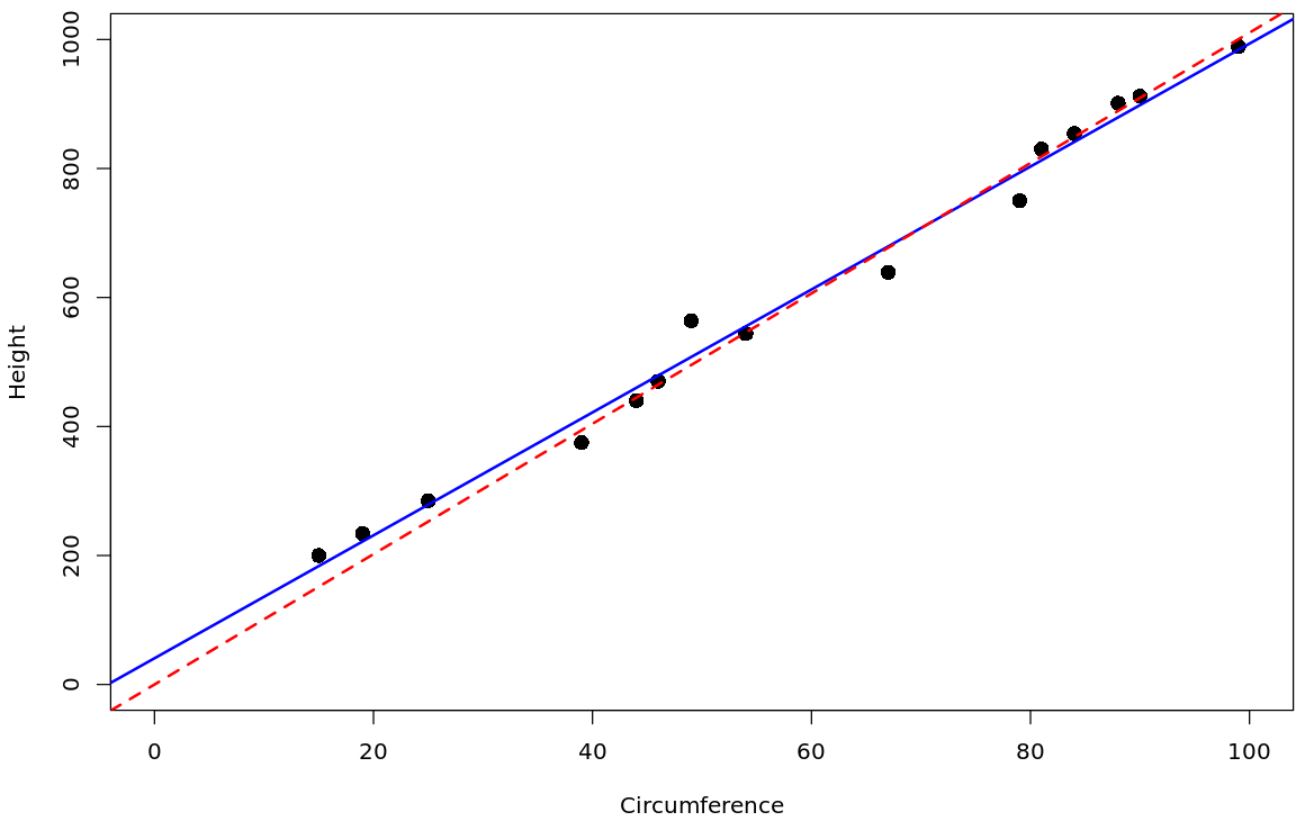
Die rot gepunktete Linie stellt das Regressionsmodell dar, das durch den Ursprung verläuft, und die blaue durchgezogene Linie stellt das gewöhnliche einfache lineare Regressionsmodell dar.

Wir können den folgenden Code in R verwenden, um die Koeffizientenschätzungen für jedes Modell zu erhalten:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

Die angepasste Gleichung für das einfache lineare Regressionsmodell lautet:

Höhe = 40,6969 + 9,5296 (Umfang)

Und die angepasste Gleichung für das Regressionsmodell über den Ursprung lautet:

Höhe = 10,1057 (Umfang)

Beachten Sie, dass die Koeffizientenschätzungen für die Umfangsvariable leicht unterschiedlich sind.

Vorsichtsmaßnahmen für die Verwendung der Regression über den Ursprung

Bevor Sie die Intercept-Regression verwenden, müssen Sie absolut sicher sein, dass ein Wert von 0 für die Prädiktorvariable einen Wert von 0 für die Antwortvariable impliziert. In vielen Fällen ist es nahezu unmöglich, dies genau zu wissen.

Und wenn Sie die Regression über den Ursprung verwenden, um einen gewissen Freiheitsgrad bei der Schätzung des Ursprungs zu bewahren, macht es selten einen wesentlichen Unterschied, ob Ihre Stichprobengröße groß genug ist.

Wenn Sie sich für die Regression über den Ursprung entscheiden, stellen Sie sicher, dass Sie Ihre Argumentation in Ihrer endgültigen Analyse oder Ihrem Bericht darlegen.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur linearen Regression:

Einführung in die einfache lineare Regression
Einführung in die multiple lineare Regression
So lesen und interpretieren Sie eine Regressionstabelle