So führen sie eine zweifaktorielle anova in sas durch

Eine zweifaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht, die zwei Variablen (manchmal auch „Faktoren“ genannt) zugeordnet wurden.

Dieses Tutorial bietet ein schrittweises Beispiel für die Durchführung einer zweifaktoriellen ANOVA in SAS.

Schritt 1: Erstellen Sie die Daten

Angenommen, ein Botaniker möchte wissen, ob das Pflanzenwachstum durch die Sonneneinstrahlung und die Häufigkeit des Gießens beeinflusst wird.

Sie pflanzt 30 Samen und lässt sie einen Monat lang unter verschiedenen Bedingungen der Sonneneinstrahlung und Bewässerungshäufigkeit wachsen. Nach einem Monat zeichnet sie die Höhe jeder Pflanze auf. Die Ergebnisse sind unten dargestellt:

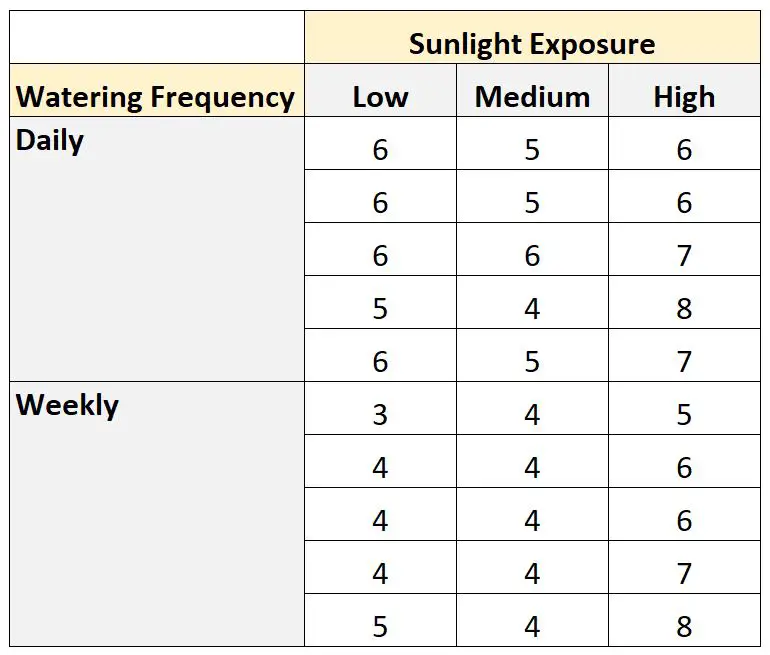
Wir können den folgenden Code verwenden, um diesen Datensatz in SAS zu erstellen:

 /*create dataset*/
data my_data;
    input water $sunlight $height;
    datalines ;
daily low 6
daily low 6
daily low 6
daily low 5
daily low 6
daily med 5
daily med 5
daily med 6
daily med 4
daily med 5
daily high 6
daily high 6
daily high 7
daily high 8
daily high 7
weekly low 3
weekly low 4
weekly low 4
weekly low 4
weekly low 5
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly high 5
weekly high 6
weekly high 6
weekly high 7
weekly high 8
;
run ;

Schritt 2: Führen Sie die zweifaktorielle ANOVA durch

Als nächstes werden wir proc ANOVA verwenden, um die zweifaktorielle ANOVA durchzuführen:

 /*perform two-way ANOVA*/
proc ANOVA data =my_data;
class water sunlight;
model height = water sunlight water*sunlight;
means water sunlight / tukey cldiff ;
run ;

Schritt 3: Interpretieren Sie die Ergebnisse

Die erste Tabelle, die wir in den Ergebnissen analysieren möchten, ist die ANOVA-Tabelle:

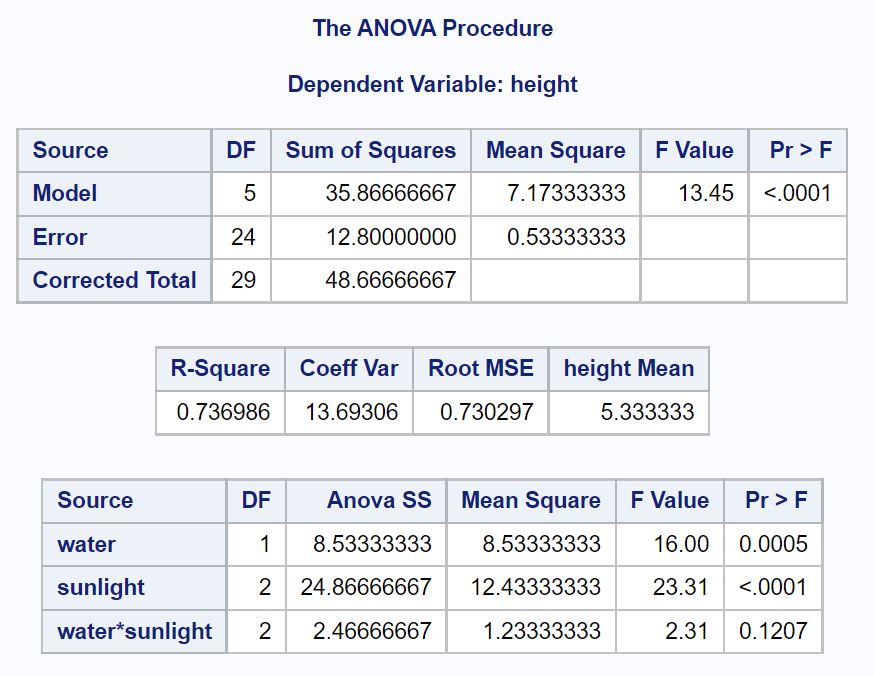
Aus dieser Tabelle können wir sehen:

• Der p-Wert für Wasser: 0,0005
• Der p-Wert für Sonnenlicht: <.0001
• Der p-Wert für die Wechselwirkung zwischen Wasser und Sonnenlicht: . 1207

Dies zeigt uns, dass Wasser und Sonnenlicht statistisch signifikante Prädiktoren für die Pflanzenhöhe sind und dass es keinen statistisch signifikanten Wechselwirkungseffekt zwischen Wasser und Sonnenlicht gibt.

Als nächstes können wir die Ergebnisse von Tukeys Post-hoc-Tests untersuchen, um festzustellen, welche Wasser- und Sonnenlichtwerte sich statistisch signifikant unterscheiden.

Zunächst schauen wir uns Tukeys Post-hoc-Vergleiche für Wasser an:

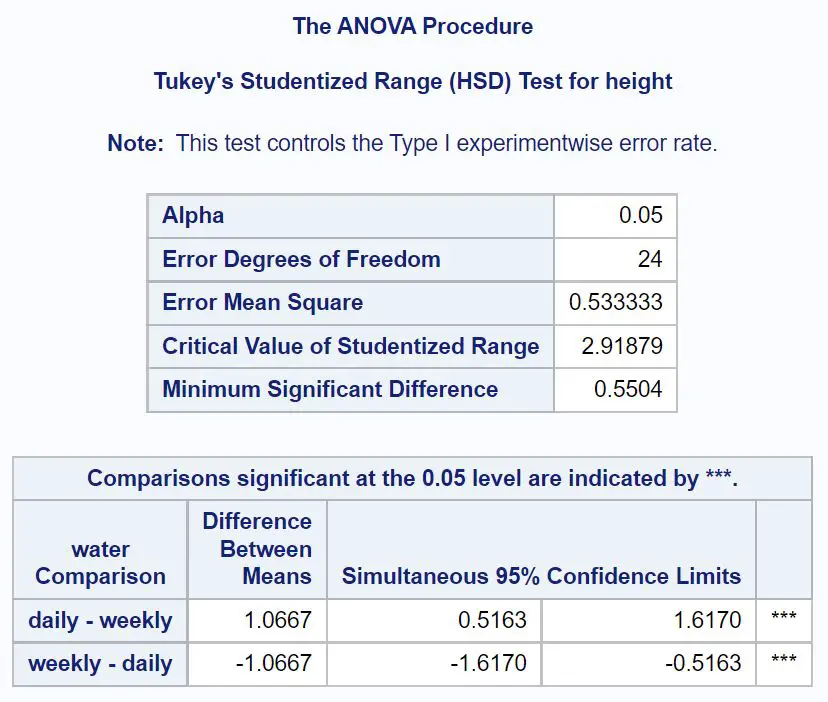
Aus den Ergebnissen können wir ersehen, dass der durchschnittliche Höhenunterschied zwischen täglich und wöchentlich bewässerten Pflanzen 1,0667 Zoll betrug.

Das 95 %-Konfidenzintervall für den Unterschied in der mittleren Größe beträgt [.5163, 1.6170] . Dies bedeutet, dass wir zu 95 % sicher sind, dass der tatsächliche Unterschied in der durchschnittlichen Höhe zwischen täglich und wöchentlich bewässerten Pflanzen zwischen 0,5163 Zoll und 1,6170 Zoll liegt.

Zuerst schauen wir uns Tukeys Post-hoc-Vergleiche für Sonnenlicht an:

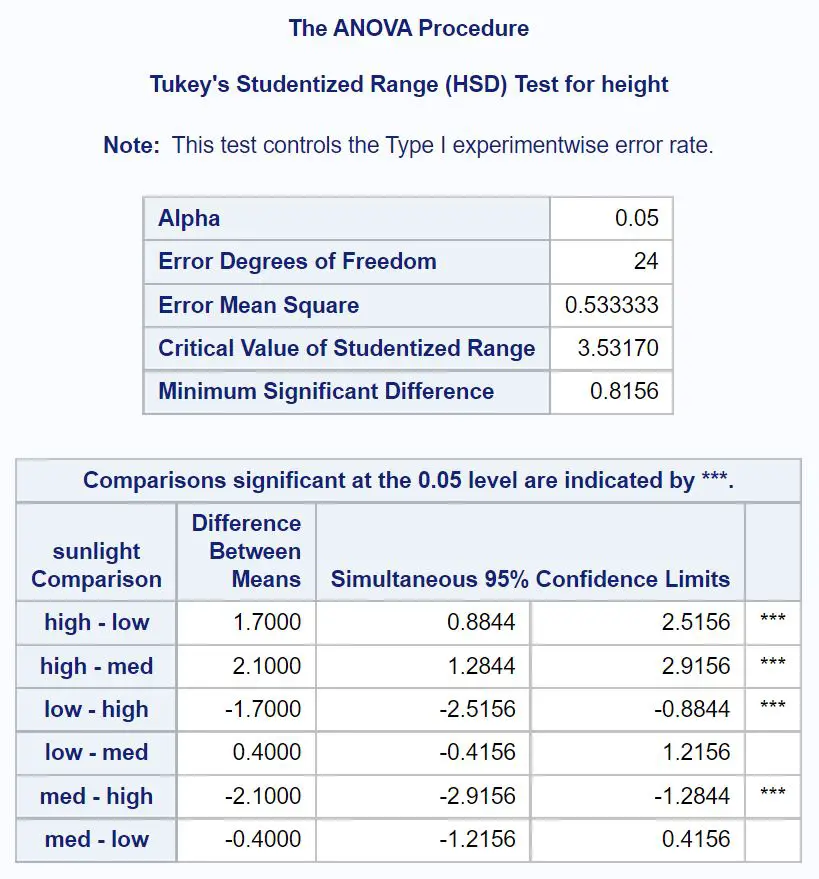
Um herauszufinden, welche Gruppenmittelwerte unterschiedlich sind, müssen wir uns ansehen, bei welchen paarweisen Vergleichen Sterne ( *** ) neben ihnen stehen.

Aus der Tabelle können wir ersehen, dass die Mittelwerte der folgenden Gruppen statistisch signifikant unterschiedlich sind:

• Hoher Sonnenschein oder geringer Sonnenschein (95 % KI = [.8844, 2.5156])
• Hoher Sonnenschein oder mittlerer Sonnenschein (95 % KI = [1,2844, 2,9156])

Schritt 4: Ergebnisse melden

Abschließend können wir über die Ergebnisse der zweifaktoriellen ANOVA berichten :

Eine Zwei-Wege-ANOVA wurde durchgeführt, um die Auswirkung der Bewässerungshäufigkeit und der Sonneneinstrahlung auf das Pflanzenwachstum zu analysieren.

Eine zweifache ANOVA ergab, dass es keine statistisch signifikante Wechselwirkung zwischen den Auswirkungen der Bewässerungshäufigkeit und der Sonneneinstrahlung gab (p = 0,1207).

Eine einfache Handeffektanalyse zeigte, dass die Bewässerungshäufigkeit einen statistisch signifikanten Einfluss auf das Pflanzenwachstum hatte (p = 0,0005).

Eine einfache Handeffektanalyse zeigte, dass Sonneneinstrahlung auch einen statistisch signifikanten Einfluss auf das Pflanzenwachstum hatte (p < 0,0001).

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu zweifaktoriellen ANOVAs:

Einführung in die zweifaktorielle ANOVA
Einfaktorielle oder zweifaktorielle ANOVA: Wann sollten sie verwendet werden?
So führen Sie manuell eine zweifaktorielle ANOVA durch