So führen sie einen t-test bei einer stichprobe in sas durch

Ein t-Test bei einer Stichprobe wird verwendet, um zu bestimmen, ob ein Populationsmittelwert einem bestimmten Wert entspricht oder nicht.

In diesem Tutorial wird erläutert, wie Sie in SAS einen Ein-Stichproben-T-Test durchführen.

Beispiel: ein Beispiel-t-Test in SAS

Angenommen, ein Botaniker möchte wissen, ob die durchschnittliche Höhe einer bestimmten Pflanzenart 15 Zoll beträgt. Sie entnimmt eine Zufallsstichprobe von 12 Pflanzen und notiert deren Höhe in Zoll.

Die Höhen sind: 14, 14, 16, 13, 12, 17, 15, 14, 15, 13, 15, 14

Führen Sie mit den folgenden Schritten einen t-Test bei einer Stichprobe durch, um festzustellen, ob die durchschnittliche Höhe dieser Pflanzenart tatsächlich 15 Zoll beträgt.

Schritt 1: Erstellen Sie die Daten.

Zunächst verwenden wir den folgenden Code, um den Datensatz in SAS zu erstellen:

 /*create dataset*/
data my_data;
    inputHeight ;
    datalines ;
14
14
16
13
12
17
15
14
15
13
15
14
;
run ;

/*print dataset*/
proc print data =my_data; 

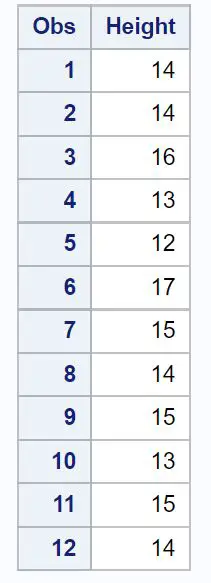
Schritt 2: Führen Sie einen T-Test bei einer Stichprobe durch.

Als nächstes verwenden wir proc ttest , um den t-Test an einem Beispiel durchzuführen:

 /*perform one sample t-test*/
proc ttest data =my_data sides = 2 alpha = 0.05 h0 = 15 ;
    varHeight ;
run ;

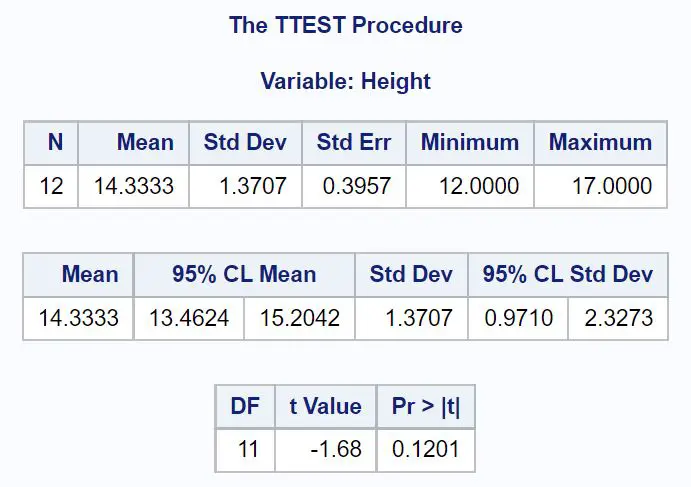
Die erste Tabelle zeigt deskriptive Statistiken für unsere Stichprobe, darunter:

• N (Gesamtbeobachtungen): 12
• Mittelwert (Stichprobendurchschnitt): 14,3333
• Std Dev (Standardabweichung der Stichprobe): 1,3707
• Standardfehler (Standardfehler, berechnet als s/ √n ): 0,3957
• Minimum (der Mindestwert): 12
• Maximum (der Maximalwert) 17

Die zweite Tabelle zeigt das 95 % -Konfidenzintervall für den wahren Grundgesamtheitsmittelwert:

• 95 %-KI für μ: [13,4624, 15,2042]

Die dritte Tabelle zeigt die T-Test-Statistik und den entsprechenden p-Wert:

• T-Test-Statistik: -1,68
• p-Wert: 0,1201

Hinweis : Die Teststatistik wurde wie folgt berechnet:

• t Teststatistik = ( x – μ) / (s/ √n )
• t-Test-Statistik = (14,3333-15) / (1,3707/√ 12 )
• T-Test-Statistik = -1,68

Denken Sie daran, dass der T-Test bei einer Stichprobe die folgenden Null- und Alternativhypothesen verwendet:

• H ₀ : μ = 15 Zoll
• H _A : μ ≠ 15 Zoll

Da der p-Wert ( .1201 ) nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.

Das bedeutet, dass wir nicht genügend Beweise dafür haben, dass die durchschnittliche Höhe einiger Pflanzenarten von 15 Zoll abweicht.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige statistische Tests in SAS durchführen:

So führen Sie einen Wilcoxon-Signed-Rank-Test in SAS durch
So führen Sie eine einfaktorielle ANOVA in SAS durch