So führen sie eine multiple lineare regression in sas durch

Die multiple lineare Regression ist eine Methode, mit der wir die Beziehung zwischen zwei oder mehr Prädiktorvariablen und einer Antwortvariablen verstehen können.

In diesem Tutorial wird erläutert, wie Sie in SAS eine multiple lineare Regression durchführen.

Schritt 1: Erstellen Sie die Daten

Angenommen, wir möchten ein multiples lineares Regressionsmodell anpassen, das die Anzahl der Lernstunden und die Anzahl der abgelegten Übungsprüfungen verwendet, um die Abschlussnote der Schüler vorherzusagen:

Prüfungsergebnis = β ₀ + β ₁ (Stunden) + β ₂ (Vorprüfungen)

Zuerst verwenden wir den folgenden Code, um einen Datensatz mit diesen Informationen für 20 Schüler zu erstellen:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Schritt 2: Führen Sie eine multiple lineare Regression durch

Als Nächstes verwenden wir proc reg , um ein multiples lineares Regressionsmodell an die Daten anzupassen:

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

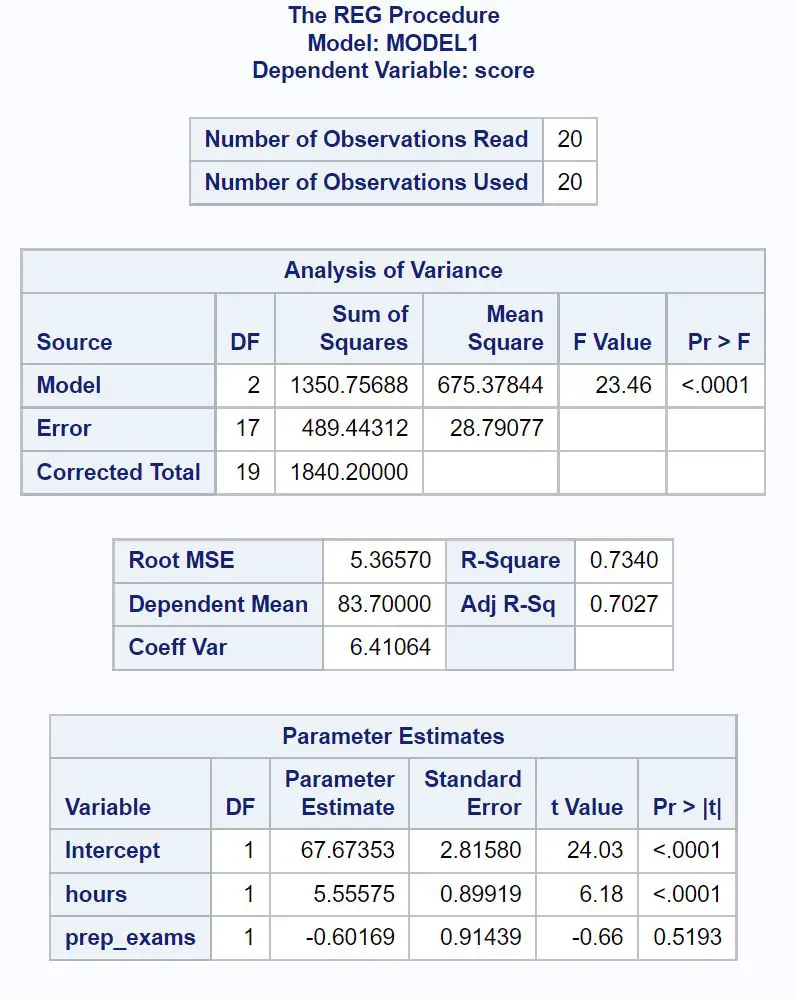
So interpretieren Sie die relevantesten Zahlen in jeder Tabelle:

Lückenanalysetabelle:

Der Gesamt- F-Wert des Regressionsmodells beträgt 23,46 und der entsprechende p-Wert ist <0,0001 .

Da dieser p-Wert kleiner als 0,05 ist, schließen wir, dass das Regressionsmodell insgesamt statistisch signifikant ist.

Modellanpassungstabelle:

Der R-Quadrat- Wert gibt uns den Prozentsatz der Variation in den Prüfungsergebnissen an, der durch die Anzahl der Lernstunden und die Anzahl der abgelegten Vorbereitungsprüfungen erklärt werden kann.

Im Allgemeinen gilt: Je größer der R-Quadrat-Wert eines Regressionsmodells, desto besser können die Prädiktorvariablen den Wert der Antwortvariablen vorhersagen.

In diesem Fall lassen sich 73,4 % der Abweichungen bei den Prüfungsergebnissen durch die Anzahl der Lernstunden und die Anzahl der abgelegten Vorbereitungsprüfungen erklären.

Es ist auch hilfreich, den Root-MSE- Wert zu kennen. Dies stellt den durchschnittlichen Abstand zwischen den beobachteten Werten und der Regressionsgeraden dar.

In diesem Regressionsmodell weichen die beobachteten Werte im Durchschnitt um 5,3657 Einheiten von der Regressionsgeraden ab.

Tabelle der Parameterschätzungen:

Wir können die Parameterschätzwerte in dieser Tabelle verwenden, um die angepasste Regressionsgleichung zu schreiben:

Prüfungsergebnis = 67,674 + 5,556*(Stunden) – 0,602*(prep_exams)

Mit dieser Gleichung können wir die geschätzte Prüfungspunktzahl eines Studenten ermitteln, basierend auf der Anzahl der Lernstunden und der Anzahl der abgelegten Übungsprüfungen.

Beispielsweise sollte ein Student, der 3 Stunden lernt und 2 Vorbereitungsprüfungen ablegt, eine Prüfungspunktzahl von 83,1 erhalten:

Geschätztes Prüfungsergebnis = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

Der p-Wert für Stunden (<0,0001) liegt unter 0,05, was bedeutet, dass ein statistisch signifikanter Zusammenhang mit dem Prüfungsergebnis besteht.

Allerdings beträgt der p-Wert für Vorbereitungsprüfungen (0,5193) nicht weniger als 0,05, was bedeutet, dass er keinen statistisch signifikanten Zusammenhang mit dem Prüfungsergebnis hat.

Möglicherweise entscheiden wir uns, vorbereitende Prüfungen aus dem Modell zu entfernen, da sie statistisch nicht signifikant sind, und führen stattdessen eine einfache lineare Regression durch, wobei wir die untersuchten Stunden als einzige Prädiktorvariable verwenden.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:

So berechnen Sie die Korrelation in SAS
So führen Sie eine einfache lineare Regression in SAS durch
So führen Sie eine einfaktorielle ANOVA in SAS durch