Hypothesentest für den mittelwert
In diesem Artikel wird erklärt, was Hypothesentests für den Mittelwert in der Statistik sind. So finden Sie die Hypothesentestformel für den Durchschnitt und zusätzlich eine Schritt für Schritt gelöste Übung.
Was ist ein Hypothesentest für den Mittelwert?
Das Testen von Hypothesen für den Mittelwert ist eine statistische Methode, die verwendet wird, um die Nullhypothese eines Populationsmittelwerts abzulehnen oder abzulehnen.
Genauer gesagt umfasst das Testen von Hypothesen für den Mittelwert die Berechnung der Teststatistik und deren Vergleich mit dem kritischen Wert, um die Nullhypothese abzulehnen oder nicht.
Es ist zu beachten, dass Hypothesentests unterschiedliche Namen haben; In der Statistik werden sie auch Hypothesenkontraste, Hypothesentests oder Signifikanztests genannt.
Hypothesentestformel für den Mittelwert
Als nächstes werden wir sehen, wie die Hypothesenteststatistik für den Mittelwert berechnet wird. Allerdings variiert die Formel geringfügig, je nachdem, ob die Varianz bekannt ist oder nicht. Daher werden wir zunächst sehen, wie sie durchgeführt wird, wenn die Varianz bekannt ist, und dann, wenn die Varianz unbekannt ist.
Mit bekannter Abweichung
Die Testhypotheseformel für den Mittelwert mit bekannter Varianz lautet:

Gold:
-

ist die Hypothesenteststatistik für den Mittelwert.
-

ist das Beispielmittel.
-

ist der vorgeschlagene Durchschnittswert.
-

ist die Populationsstandardabweichung.
-

ist die Stichprobengröße.
Sobald die Hypothesenteststatistik für den Mittelwert berechnet ist, sollte das Ergebnis so interpretiert werden, dass es die Nullhypothese zurückweist oder ablehnt:
- Wenn der Hypothesentest für den Mittelwert zweiseitig ist, wird die Nullhypothese abgelehnt, wenn der Absolutwert der Statistik größer als der kritische Wert Z α/2 ist.
- Wenn der Hypothesentest für den Mittelwert mit dem rechten Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn die Statistik größer als der kritische Wert Z α ist.
- Wenn der Hypothesentest für den Mittelwert mit dem linken Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn die Statistik kleiner als der kritische Wert -Z α ist.
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0e2ccadfc369eb7543b8f86dfccc528e_l3.png)
In diesem Fall werden die kritischen Werte aus der standardisierten Normalverteilungstabelle gewonnen.
Mit unbekannter Varianz
Die Testhypotheseformel für den Mittelwert mit unbekannter Varianz lautet:

Gold:
-

ist die Hypothesenteststatistik für den Mittelwert, der durch eine Student-t-Verteilung definiert ist.
-

ist das Beispielmittel.
-

ist der vorgeschlagene Durchschnittswert.
-

ist die Standardabweichung der Stichprobe.
-

ist die Stichprobengröße.
Wie zuvor muss das berechnete Ergebnis der Teststatistik mit dem kritischen Wert interpretiert werden, um die Nullhypothese abzulehnen oder nicht:
- Wenn der Hypothesentest für den Mittelwert zweiseitig ist, wird die Nullhypothese abgelehnt, wenn der Absolutwert der Statistik größer als der kritische Wert t α/2|n-1 ist.
- Wenn der Hypothesentest für den Mittelwert mit dem rechten Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn die Statistik größer als der kritische Wert t α|n-1 ist.
- Wenn der Hypothesentest für den Mittelwert mit dem linken Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn die Statistik kleiner als der kritische Wert -t α|n-1 ist.
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
Wenn die Varianz unbekannt ist, werden die kritischen Testwerte aus der Student-Verteilungstabelle ermittelt.
Beispiel aus der Praxis für die Prüfung von Hypothesen auf den Mittelwert
Um das Konzept des Hypothesentests für den Grundgesamtheitsmittelwert vollständig zu verstehen, können Sie sich unten ein reales Beispiel für diese Art von Hypothesentests ansehen.
- Ein Technologieunternehmen gibt an, dass der Akku des von ihm verkauften Laptops 6 Stunden hält. Wir überprüfen, ob diese Hypothese falsch ist, indem wir einen Hypothesentest mit einem Signifikanzniveau α = 0,05 durchführen. Zu diesem Zweck wird beschlossen, 20 Einheiten zu kaufen und die Akkulaufzeit jedes Computers zu beobachten (Werte werden in Stunden ausgedrückt):
5,2 5,9 7,1 4,2 6,5
8,5 4,6 6,8 6,9 5,8
5,1 6,5 7,0 5,3 6,2
5,7 6,6 7,5 5,1 6,1
In diesem Fall lauten die Null- und Alternativhypothese des Hypothesentests über den Mittelwert wie folgt:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-329ffe392783b8bee1eef642d1a45f53_l3.png)
Um die Teststatistik zu bestimmen, müssen wir zunächst den Stichprobenmittelwert und die Stichprobenstandardabweichung berechnen:
![]()
Da wir die Populationsvarianz nicht kennen, müssen wir zum Erhalten der Teststatistik die Hypothesentestformel für den Mittelwert mit unbekannter Varianz anwenden:

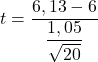
![]()
Jetzt müssen wir den kritischen Wert des Hypothesentests ermitteln, also suchen wir in der Student-t-Verteilungstabelle nach dem entsprechenden Wert. Die Freiheitsgrade von Student’s t sind eins kleiner als die Stichprobengröße (20-1=19) und andererseits beträgt die entsprechende Wahrscheinlichkeit die Hälfte des Signifikanzniveaus (0,05/2=0,025), da es zweiseitig ist Hypothesentest.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e85692dfb2fb2522025566dc205b8117_l3.png)
Zusammenfassend lässt sich sagen, dass die Nullhypothese nicht abgelehnt wird, da es sich um einen zweiseitigen Hypothesentest handelt und der absolute Wert der Teststatistik kleiner als der kritische Wert ist, sondern die Alternativhypothese.
![]()
Hypothesentest auf Mittelwertunterschiede
Der Mittelwertdifferenz-Hypothesetest wird verwendet, um die Nullhypothese, dass die Mittelwerte zweier Grundgesamtheiten gleich sind, abzulehnen oder zu akzeptieren.
Somit lautet die Nullhypothese eines Hypothesentests für die Differenz zweier Mittelwerte immer wie folgt:
![]()
Während die Alternativhypothese eine der folgenden drei sein kann:
![Rendered by QuickLaTeX.com \begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c612ac7651faad9faa195f37fdf6edef_l3.png)
Dann lautet die Formel zur Berechnung der Hypothesenteststatistik für die Mittelwertdifferenz bei bekannter Varianz :
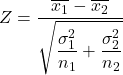
Gold:
-

ist die Hypothesenteststatistik für die Differenz zweier Mittelwerte mit bekannter Varianz, die einer Standardnormalverteilung folgt.
-

ist der Mittelwert von Stichprobe 1.
-

ist der Mittelwert von Stichprobe 2.
-

ist die Varianz der Grundgesamtheit 1.
-

ist die Varianz der Grundgesamtheit 2.
-

ist Stichprobengröße 1.
-

ist Stichprobengröße 2.
Andererseits lautet die Formel zur Berechnung der Hypothesenteststatistik für die Mittelwertdifferenz bei unbekannter Varianz wie folgt:
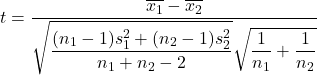
Gold:
-

ist die Hypothesenteststatistik für die Differenz zweier Mittelwerte mit unbekannter Varianz, die der Student-t-Verteilung folgt.
-

ist der Mittelwert von Stichprobe 1.
-

ist der Mittelwert von Stichprobe 2.
-

ist die Varianz von Stichprobe 1.
-

ist die Varianz von Stichprobe 2.
-

ist Stichprobengröße 1.
-

ist Stichprobengröße 2.