Hypothesentest auf proportionalität

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erläutert, welchen Anteil das Testen von Hypothesen in der Statistik hat. Sie finden daher die Formel für den Hypothesentest zum Verhältnis und zusätzlich eine Schritt-für-Schritt-Übung, um die Durchführung vollständig zu verstehen.

Was ist ein Hypothesentest für Proportionen?

Der Anteilshypothesetest ist eine statistische Methode, mit der ermittelt wird, ob die Nullhypothese eines Bevölkerungsanteils abgelehnt werden soll oder nicht.

Abhängig vom Wert der Hypothesenteststatistik für den Anteil und das Signifikanzniveau wird die Nullhypothese also abgelehnt oder akzeptiert.

Beachten Sie, dass Hypothesentests auch als Hypothesenkontraste, Hypothesentests oder Signifikanztests bezeichnet werden können.

Hypothesentestformel für Proportionen

Die Hypothesenteststatistik für den Anteil entspricht der Differenz im Stichprobenanteil minus dem vorgeschlagenen Wert des Anteils dividiert durch die Standardabweichung des Anteils.

Die Testhypotheseformel für den Anteil lautet daher:

$\displaystyle Z=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}$

Gold:

$Z$

ist die Hypothesenteststatistik für den Anteil.
$\widehat{p}$

ist der Stichprobenanteil.
$p$

ist der Wert des vorgeschlagenen Anteils.
$n$

ist die Stichprobengröße.
$\displaystyle\sqrt{\frac{p(1-p)}{n}}$

ist die Standardabweichung des Anteils.

Beachten Sie, dass es nicht ausreicht, die Hypothesenteststatistik für den Anteil zu berechnen, sondern das Ergebnis anschließend interpretiert werden muss:

Wenn der Hypothesentest für den Anteil zweiseitig ist, wird die Nullhypothese abgelehnt, wenn der Absolutwert der Statistik größer als der kritische Wert Z _α/2 ist.
Wenn der Hypothesentest für den Anteil mit dem rechten Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn die Statistik größer als der kritische Wert Z _α ist.
Wenn der Hypothesentest für den Anteil mit dem linken Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn die Statistik kleiner als der kritische Wert -Z _α ist.

$\begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

Denken Sie daran, dass kritische Werte leicht aus der Normalverteilungstabelle ermittelt werden können.

➤ Siehe: Normalverteilungstabelle

Beispiel für Hypothesentests auf Proportionen

Sobald wir die Definition des Hypothesentests auf Proportionen und die dazugehörige Formel gesehen haben, werden wir ein Beispiel lösen, um das Konzept besser zu verstehen.

Nach Angaben des Herstellers ist ein Medikament gegen eine bestimmte Krankheit zu 70 % wirksam. Im Labor testen wir die Wirksamkeit dieses Medikaments, da Forscher davon ausgehen, dass das Verhältnis unterschiedlich ist. Dafür wird das Medikament an einer Stichprobe von 1.000 Patienten getestet und 641 Menschen werden geheilt. Führen Sie einen Hypothesentest für den Bevölkerungsanteil mit einem Signifikanzniveau von 5 % durch, um die Hypothese der Forscher abzulehnen oder nicht.

In diesem Fall lauten die Nullhypothese und die Alternativhypothese des Hypothesentests für den Bevölkerungsanteil:

$\begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}$

Der Anteil der Personen in der Stichprobe, die durch das Medikament geheilt wurden, beträgt:

$\widehat{p}=\cfrac{641}{1000}=0,641$

Wir berechnen die Hypothesenteststatistik für den Anteil, indem wir die oben gezeigte Formel anwenden:

$\begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}$

Da das Signifikanzniveau andererseits bei 0,05 liegt und es sich um einen zweiseitigen Hypothesentest handelt, beträgt der kritische Wert des Tests 1,96.

$Z_{0,025}=1,96$

➤ Siehe: Signifikanzniveau 0,05

Zusammenfassend lässt sich sagen, dass der absolute Wert der Teststatistik größer als der kritische Wert ist, sodass wir die Nullhypothese ablehnen und die Alternativhypothese akzeptieren.

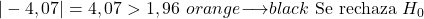$|-4,07|=4,07>1,96 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_0″ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“424″ style=“vertical-align: -5px;“></p> </p> <div style=$ ➤ Siehe: Hypothesentest für den Mittelwert

Hypothesentest für zwei Stichprobenanteile

Hypothesentests für Anteile zweier Stichproben werden verwendet, um die Nullhypothese, dass die Anteile zweier unterschiedlicher Populationen gleich sind, abzulehnen oder zu akzeptieren.

Daher lautet die Nullhypothese eines Hypothesentests für Anteile bei zwei Stichproben immer:

$H_0: p_1=p_2$

Während die Alternativhypothese eine von drei Optionen sein kann:

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.

Und die Formel zur Berechnung der Hypothesenteststatistik für zwei Stichprobenanteile lautet:

$\displaystyle Z=\frac{\displaystyle \frac{x_1}{n_1}-\frac{x_2}{n_2}}{\displaystyle \sqrt{p(1-p)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$

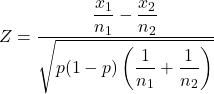
Gold:

$Z$

ist die Hypothesenteststatistik für Anteile mit zwei Stichproben.
$x_1$

ist die Anzahl der Ergebnisse in Stichprobe 1.
$x_2$

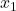
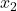
ist die Anzahl der Ergebnisse in Stichprobe 2.
$n_1$

ist Stichprobengröße 1.
$n_2$

ist Stichprobengröße 2.
$p$

ist der kombinierte Anteil der beiden Stichproben.

Hypothesentest für k Stichprobenanteile

Bei einem Hypothesentest über Anteile von k Stichproben besteht das Ziel darin, festzustellen, ob alle Anteile der verschiedenen Populationen gleich sind oder ob es im Gegenteil unterschiedliche Anteile gibt. Daher lauten die Nullhypothese und die Alternativhypothese in diesem Fall:

$\begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}$

In diesem Fall wird der kombinierte Anteil aller Stichproben wie folgt berechnet:

$p=\cfrac{\displaystyle\sum_{i=1}^k x_i}{\displaystyle\sum_{i=1}^k n_i}=\cfrac{x_1+x_2+\dots+x_k}{n_1+n_2+\dots+n_k}$

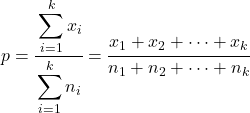
Die Formel zum Ermitteln der Hypothesenteststatistik für k Stichprobenanteile lautet:

$\displaystyle \chi^2 =\sum_{i=1}^k \frac{(x_i-e_i)^2}{e_i}$

$\displaystyle\chi^2 = \frac{(x_1-e_1)^2}{e_1} +\frac{(x_2-e_2)^2}{e_2} +\dots+\frac{(x_k-e_k)^2}{e_k}$

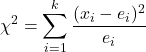
Gold:

$\chi^2$

ist die Hypothesenteststatistik für k Stichprobenanteile. In diesem Fall folgt die Statistik einer Chi-Quadrat-Verteilung.
$x_i$

ist die Anzahl der Ergebnisse in Stichprobe i.
$n_i$

ist die Stichprobengröße i.
$p$

ist der kombinierte Anteil aller Proben.
$e_i$

ist die Anzahl der von Stichprobe i erwarteten Treffer. Er wird durch Multiplikation des kombinierten Anteils berechnet

$p$

nach Stichprobengröße

$n_i$

.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Was ist ein Hypothesentest für Proportionen?

Hypothesentestformel für Proportionen

Beispiel für Hypothesentests auf Proportionen

Hypothesentest für zwei Stichprobenanteile

Hypothesentest für k Stichprobenanteile

Über den Autor

Dr. Benjamin Anderson

Einen Kommentar hinzufügen