So führen sie eine logistische regression in sas durch
Die logistische Regression ist eine Methode, mit der wir ein Regressionsmodell anpassen können, wenn die Antwortvariable binär ist.
Die logistische Regression verwendet eine als Maximum-Likelihood-Schätzung bekannte Methode, um eine Gleichung der folgenden Form zu finden:
log[p(X) / (1 – p(X))] = β 0 + β 1 X 1 + β 2 X 2 + … + β p
Gold:
- X j : die j -te Vorhersagevariable
- β j : Schätzung des Koeffizienten für die j -te Vorhersagevariable
Die Formel auf der rechten Seite der Gleichung sagt die logarithmische Wahrscheinlichkeit voraus, dass die Antwortvariable den Wert 1 annimmt.
Das folgende Schritt-für-Schritt-Beispiel zeigt, wie ein logistisches Regressionsmodell in SAS angepasst wird.
Schritt 1: Erstellen Sie den Datensatz
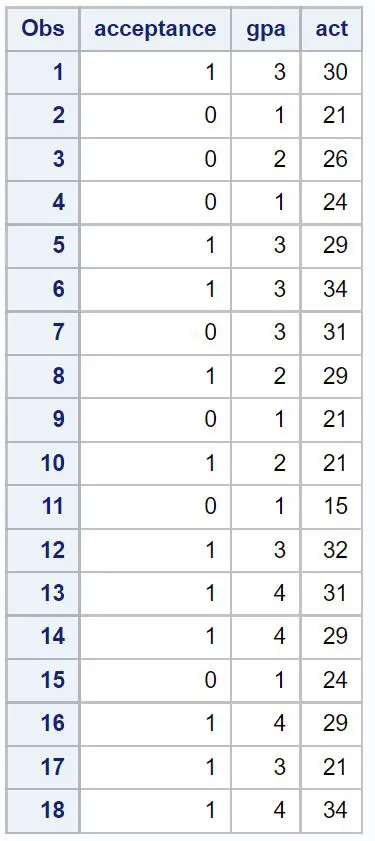
Zunächst erstellen wir einen Datensatz mit Informationen zu den folgenden drei Variablen für 18 Studierende:
- Aufnahme in eine bestimmte Hochschule (1 = ja, 0 = nein)
- GPA (Skala von 1 bis 4)
- ACT-Score (Skala von 1 bis 36)
/*create dataset*/ data my_data; input acceptance gpa act; datalines ; 1 3 30 0 1 21 0 2 26 0 1 24 1 3 29 1 3 34 0 3 31 1 2 29 0 1 21 1 2 21 0 1 15 1 3 32 1 4 31 1 4 29 0 1 24 1 4 29 1 3 21 1 4 34 ; run ; /*view dataset*/ proc print data =my_data;
Schritt 2: Passen Sie das logistische Regressionsmodell an
Als Nächstes verwenden wir die Proc-Logistik , um das logistische Regressionsmodell anzupassen, wobei wir „Akzeptanz“ als Antwortvariable und „gpa“ und „Handlung“ als Prädiktorvariablen verwenden.
Hinweis : „Abnehmend“ muss angegeben werden, damit SAS die Wahrscheinlichkeit vorhersagen kann, dass die Antwortvariable den Wert 1 annimmt. Standardmäßig sagt SAS die Wahrscheinlichkeit voraus, dass die Antwortvariable den Wert 0 annimmt.
/*fit logistic regression model*/
proc logistic data =my_data descending ;
model acceptance = gpa act;
run ;
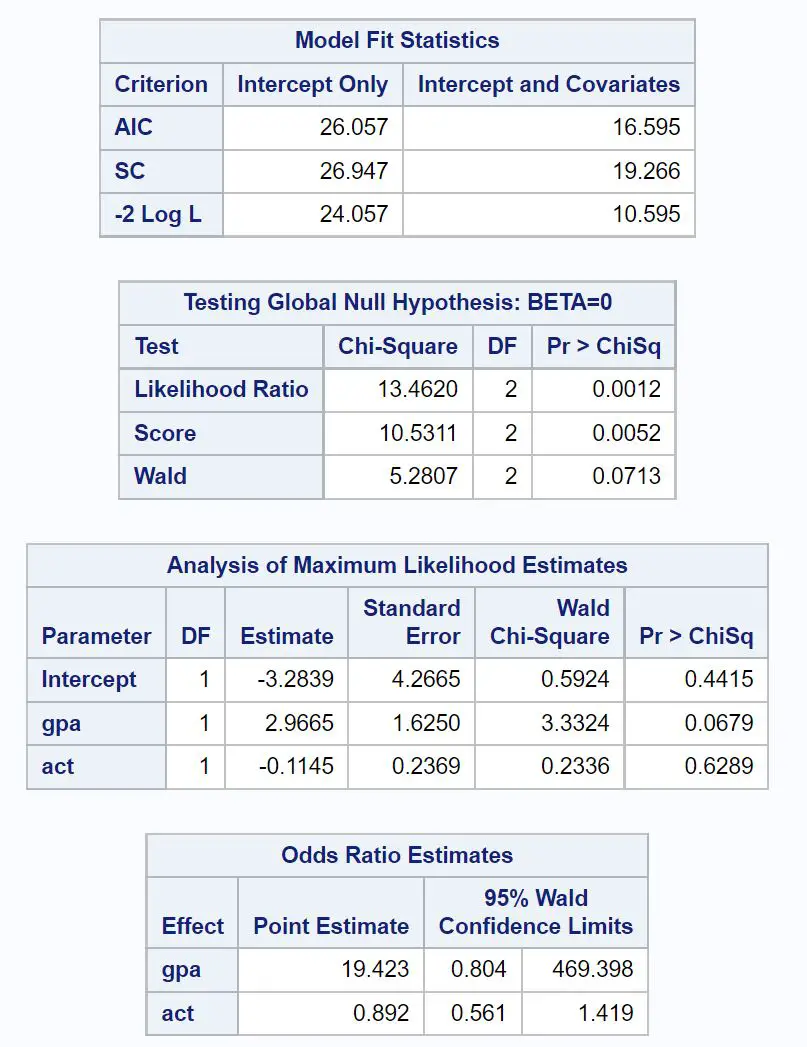
Die erste interessante Tabelle trägt den Titel „Model Fit Statistics“ .
Aus dieser Tabelle können wir den AIC-Wert des Modells ersehen, der 16,595 beträgt. Je niedriger der AIC-Wert, desto besser kann das Modell die Daten anpassen.
Es gibt jedoch keinen Schwellenwert dafür, was als „guter“ AIC-Wert gilt. Vielmehr verwenden wir AIC, um die Anpassung mehrerer Modelle an denselben Datensatz zu vergleichen. Das Modell mit dem niedrigsten AIC-Wert gilt allgemein als das beste.
Die nächste interessante Tabelle trägt den Titel Testing the Global Null Hypothesis: BETA=0 .
Aus dieser Tabelle können wir den Chi-Quadrat-Wert des Likelihood-Verhältnisses von 13,4620 mit einem entsprechenden p-Wert von 0,0012 ersehen.
Da dieser p-Wert kleiner als 0,05 ist, bedeutet dies, dass das logistische Regressionsmodell als Ganzes statistisch signifikant ist.
Als Nächstes können wir die Koeffizientenschätzungen in der Tabelle mit dem Titel „Analyse der Maximum-Likelihood-Schätzungen“ analysieren.
Aus dieser Tabelle können wir die Koeffizienten für GPA und Act ersehen, die die durchschnittliche Änderung der logarithmischen Wahrscheinlichkeit einer Aufnahme ins College bei einer Erhöhung um eine Einheit in jeder Variablen angeben.
Zum Beispiel:
- Eine Erhöhung des GPA-Werts um eine Einheit ist mit einer durchschnittlichen Erhöhung der logarithmischen Wahrscheinlichkeit, ins College aufgenommen zu werden, um 2,9665 verbunden.
- Ein Anstieg des ACT-Scores um eine Einheit ist mit einem durchschnittlichen Rückgang der logarithmischen Wahrscheinlichkeit, ins College aufgenommen zu werden, um 0,1145 verbunden.
Die entsprechenden p-Werte im Ergebnis geben uns auch eine Vorstellung davon, wie effektiv jede Prädiktorvariable bei der Vorhersage der Akzeptanzwahrscheinlichkeit ist:
- GPA-P-Wert: 0,0679
- ACT-P-Wert: 0,6289
Dies zeigt uns, dass der Notendurchschnitt (GPA) ein statistisch signifikanter Prädiktor für die Hochschulakzeptanz zu sein scheint, während der ACT-Score statistisch nicht signifikant zu sein scheint.
Zusätzliche Ressourcen
In den folgenden Tutorials wird erläutert, wie andere Regressionsmodelle in SAS angepasst werden:
So führen Sie eine einfache lineare Regression in SAS durch
So führen Sie eine multiple lineare Regression in SAS durch