Kritischer wert

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erläutert, was der kritische Wert in der Statistik ist und wie er beim Testen von Hypothesen interpretiert werden sollte. Ebenso können Sie sehen, wie der kritische Wert berechnet wird, sowie einige konkrete Beispiele.

Was ist der kritische Wert?

Der kritische Wert ist der Punkt in der Verteilung der Teststatistik, der den Bereich der Ablehnung der Nullhypothese von ihrem Akzeptanzbereich trennt. Mit anderen Worten: Der kritische Wert ist der Wert der Verteilung des statistischen Tests, der die Grenze des Ablehnungsbereichs (oder des kritischen Bereichs) markiert.

Normalerweise wird der kritische Wert durch das Symbol Z _α/2 dargestellt, da die häufigste Referenzverteilung normalerweise die Standardnormalverteilung ist.

Im Allgemeinen sind einseitige Tests von entscheidender Bedeutung, da der Ablehnungsbereich einen einzelnen Rand der Verteilung darstellt. Andererseits haben zweiseitige Tests zwei kritische Werte, da der Ablehnungsbereich beiden Enden der Verteilung entspricht.

Bei Konfidenzintervallen sind kritische Werte die Punkte in der Referenzverteilung, die die Grenzen des Konfidenzintervalls markieren.

So berechnen Sie den kritischen Wert

Wir werden dann sehen, wie die häufigsten kritischen Werte berechnet werden. Der kritische Wert von Z und der kritische Wert von t werden für das Konfidenzintervall des Mittelwerts berechnet. Der einzige Unterschied besteht darin, dass der kritische Wert von Z berechnet wird, wenn die Standardabweichung der Grundgesamtheit bekannt ist, und stattdessen der kritische Wert von t verwendet wird wenn nur die Daten für eine Probe bekannt sind.

Kritischer Wert von Z

Der kritische Wert von Z wird verwendet, um die Grenzen des Konfidenzintervalls für den Mittelwert zu bestimmen. Genauer gesagt wird es nur verwendet, wenn Sie die Standardabweichung der Grundgesamtheit kennen.

Um den kritischen Wert von Z zu berechnen, muss der Wert, der der Wahrscheinlichkeit des halben Signifikanzniveaus entspricht, in der Standardnormalverteilungstabelle gefunden werden.

Wenn wir beispielsweise ein Konfidenzintervall für den Mittelwert mit einem Konfidenzniveau von 95 % ermitteln möchten, bedeutet dies, dass das Signifikanzniveau 5 % beträgt. Daher ist es notwendig, in der Tabelle der Standardnormalverteilung zu sehen, welcher Wert einer Wahrscheinlichkeit von 2,5 % entspricht, da das Konfidenzintervall für den Mittelwert zweiseitig ist.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

Unten sehen Sie eine Tabelle mit den am häufigsten verwendeten kritischen Z-Werten:

Konfidenzniveau (1-α)	Signifikanzniveau (α)	Kritischer Wert (Z _α/2 )
0,80	0,20	1.282
0,85	0,15	1.440
0,90	0,10	1.645
0,95	0,05	1960
0,99	0,01	2.576
0,995	0,005	2.807
0,999	0,001	3.291

Kritischer Wert von t

Der kritische t-Wert wird verwendet, um die Grenzen des Konfidenzintervalls für den Mittelwert zu ermitteln, wenn die Standardabweichung der Grundgesamtheit unbekannt ist.

Um den kritischen Wert von t zu berechnen, muss der Wert, der der Wahrscheinlichkeit des halben Signifikanzniveaus entspricht, in der Student-t-Verteilungstabelle gefunden werden, wobei zu berücksichtigen ist, dass die Freiheitsgrade der Student-t-Verteilung eine Einheit sind. als die Stichprobengröße.

Wenn wir beispielsweise das Konfidenzintervall mit einem Konfidenzniveau von 95 % ermitteln möchten und die Stichprobengröße 8 beträgt, müssen wir auf die Student-t-Verteilungstabelle zugreifen und sehen, welcher Wert t _0,025|7 entspricht.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}$

➤ Siehe: So berechnen Sie das Konfidenzintervall des Mittelwerts

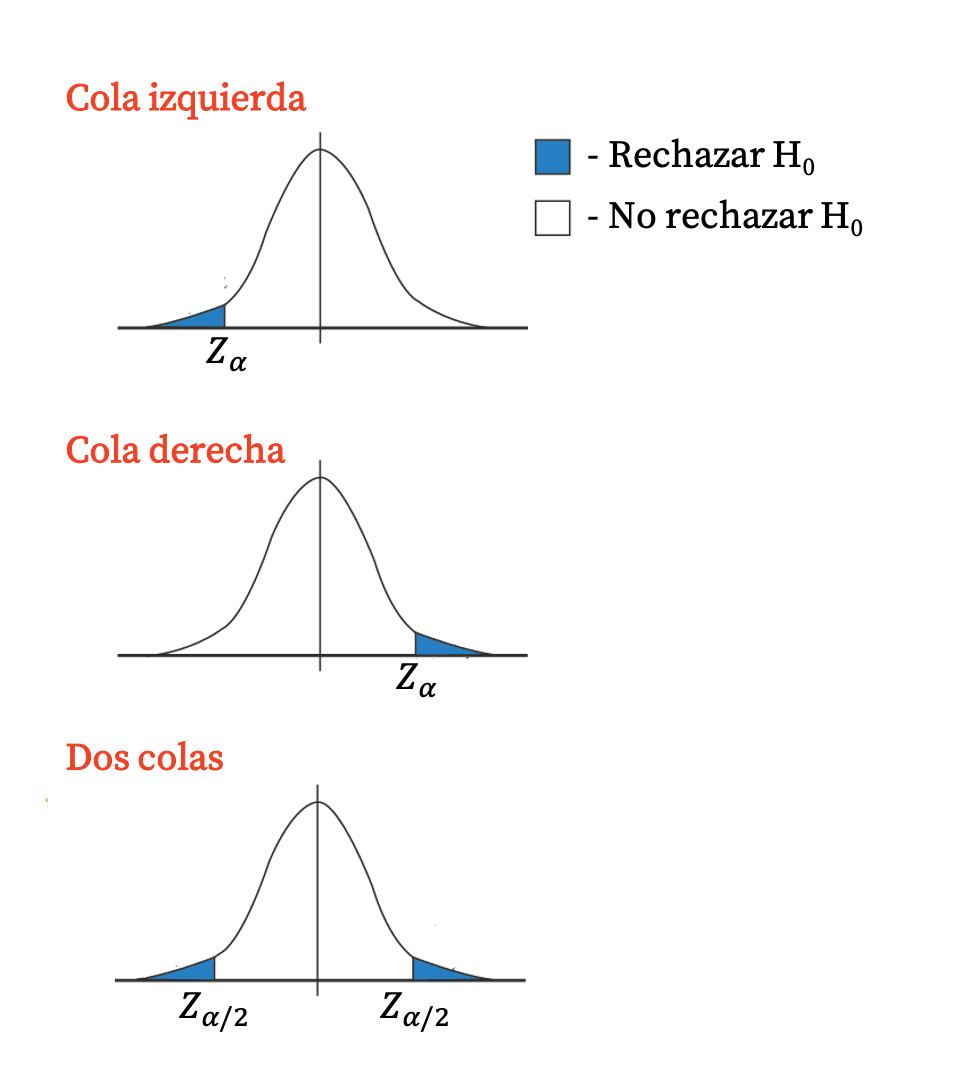
Der kritische Wert beim Hypothesentest

Der kritische Wert kann auch beim Hypothesentest verwendet werden, um die Nullhypothese abzulehnen (und die Alternativhypothese zu akzeptieren) oder die Alternativhypothese abzulehnen (und die Nullhypothese zu akzeptieren).

Liegt der Wert der dem p-Wert entsprechenden Verteilung der Teststatistik innerhalb des durch die kritischen Werte markierten Intervalls, wird die Nullhypothese nicht verworfen (die Alternativhypothese wird verworfen).
Liegt der Wert der Verteilung der Teststatistik entsprechend dem p-Wert außerhalb des durch die kritischen Werte markierten Intervalls, wird die Nullhypothese verworfen (die Alternativhypothese wird akzeptiert).

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen