So ermitteln sie den median gruppierter daten: mit beispielen

Wir möchten oft den Median der auf irgendeine Weise gruppierten Daten berechnen.

Denken Sie daran, dass der Median den Wert darstellt, der direkt in der Mitte eines Datensatzes liegt, wenn alle Werte vom kleinsten zum größten geordnet sind.

Angenommen, wir haben die folgenden gruppierten Daten:

Obwohl es nicht möglich ist, den genauen Median zu berechnen, da wir die Rohdatenwerte nicht kennen, ist es möglich, den Median mithilfe der folgenden Formel zu schätzen:

Median der gruppierten Daten = L + W[(N/2 – C) / F]

Gold:

• L : Untere Grenze der Medianklasse
• W : Mittlere Klassenbreite
• N : Gesamtfrequenz
• C : Kumulierte Häufigkeit bis zur Medianklasse
• F : Mittlere Klassenhäufigkeit

Hinweis : Die Mittelklasse ist die Klasse, die den Wert bei N/2 enthält. Im obigen Beispiel gibt es N = 23 Gesamtwerte. Somit liegt der Medianwert bei Position 23/2 = 11,5, was in der Klasse 21-30 liegen würde.

Die folgenden Beispiele zeigen, wie der Median gruppierter Daten in verschiedenen Szenarien berechnet wird.

Beispiel 1: Berechnen Sie den Median gruppierter Daten

Angenommen, wir haben die folgende Häufigkeitsverteilung, die zeigt, wie die Prüfung von 40 Schülern einer bestimmten Klasse bewertet wurde:

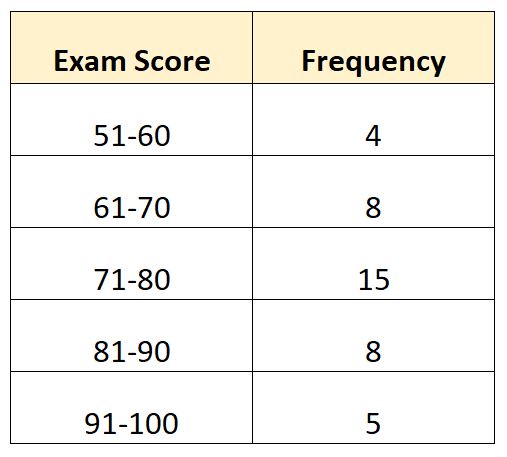
In diesem Beispiel gibt es N = 40 Gesamtwerte. Der Medianwert liegt also in der Klasse, in der 40/2 = 20 liegt. Der 20. größte Wert wäre in der Klasse 71-80 .

Mit diesem Wissen können wir die folgenden Werte berechnen:

• L : Untere Mittelschichtsgrenze: 71
• W : Mittlere Klassenbreite: 9
• N : Gesamthäufigkeit: 40
• C : Kumulierte Häufigkeit bis zur Medianklasse: 12
• F : Mittlere Unterrichtshäufigkeit: 15

Wir können diese Werte in die Formel einfügen, um den Median der Verteilung zu berechnen:

• Median = L + W[(N/2 – C) / F]
• Median = 71 + 9[(40/2 – 12) / 15]
• Median = 75,8

Wir schätzen die mittlere Prüfungspunktzahl auf 75,8 .

Beispiel 2: Berechnen Sie den Median gruppierter Daten

Angenommen, wir haben die folgende Häufigkeitsverteilung, die die Anzahl der pro Spiel von 60 Basketballspielern erzielten Punkte zeigt:

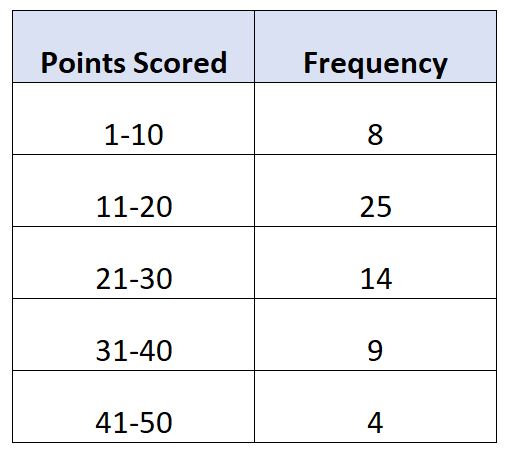
In diesem Beispiel gibt es N = 60 Gesamtwerte. Somit liegt der Medianwert in der Klasse, in der 60/2 = 30 liegt. Der 30. größte Wert wäre in der Klasse 11-20 .

Mit diesem Wissen können wir die folgenden Werte berechnen:

• L : Untere Mittelschichtsgrenze: 11
• W : Mittlere Klassenbreite: 9
• N : Gesamtfrequenz: 60
• C : Kumulierte Häufigkeit bis zur Medianklasse: 8
• F : Mittlere Unterrichtshäufigkeit: 25

Wir können diese Werte in die Formel einfügen, um den Median der Verteilung zu berechnen:

• Median = L + W[(N/2 – C) / F]
• Median = 11 + 9[(60/2 – 8) / 25]
• Median = 18,92

Wir schätzen die mittlere Prüfungspunktzahl auf 18,92 .

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige Vorgänge mit gruppierten Daten durchführen:

So ermitteln Sie den Mittelwert und die Standardabweichung gruppierter Daten
So finden Sie den gruppierten Datenmodus
So berechnen Sie die Perzentilrangfolge für gruppierte Daten