So erstellen sie eine roc-kurve in sas

Die logistische Regression ist eine Methode, mit der wir ein Regressionsmodell anpassen können, wenn die Antwortvariable binär ist.

Um zu bewerten, wie gut ein logistisches Regressionsmodell zu einem Datensatz passt, können wir uns die folgenden zwei Metriken ansehen:

• Sensitivität: Wahrscheinlichkeit, dass das Modell ein positives Ergebnis für eine Beobachtung vorhersagt, obwohl das Ergebnis tatsächlich positiv ist. Dies wird auch als „True-Positive-Rate“ bezeichnet.
• Spezifität: Die Wahrscheinlichkeit, dass das Modell ein negatives Ergebnis für eine Beobachtung vorhersagt, obwohl das Ergebnis tatsächlich negativ ist. Dies wird auch als „echte Negativrate“ bezeichnet.

Eine Möglichkeit, diese beiden Messungen zu visualisieren, besteht darin, eine ROC-Kurve zu erstellen, die für „Receiver Operating Characteristic“-Kurve steht. Dies ist ein Diagramm, das die Sensitivität und Spezifität eines logistischen Regressionsmodells anzeigt.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie eine ROC-Kurve in SAS erstellt und interpretiert wird.

Schritt 1: Erstellen Sie den Datensatz

Zunächst erstellen wir einen Datensatz mit Informationen zu den folgenden Variablen für 18 Studierende:

• Aufnahme in eine bestimmte Hochschule (1 = ja, 0 = nein)
• GPA (Skala von 1 bis 4)
• ACT-Score (Skala von 1 bis 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

Schritt 2: Passen Sie das logistische Regressionsmodell an und erstellen Sie eine ROC-Kurve

Als Nächstes verwenden wir die Proc-Logistik , um das logistische Regressionsmodell anzupassen, wobei wir „Akzeptanz“ als Antwortvariable und „gpa“ und „Handlung“ als Prädiktorvariablen verwenden.

Wir werden die Verringerung angeben, damit SAS die Wahrscheinlichkeit vorhersagen kann, dass die Antwortvariable den Wert 1 annimmt.

Wir werden auch plots(only)=roc verwenden, um die ROC-Kurve für das Modell zu erstellen:

 /*fit logistic regression model & create ROC curve*/
proc logistic data =my_data descending plots ( only )=roc;
  model acceptance = gpa act;
run ;

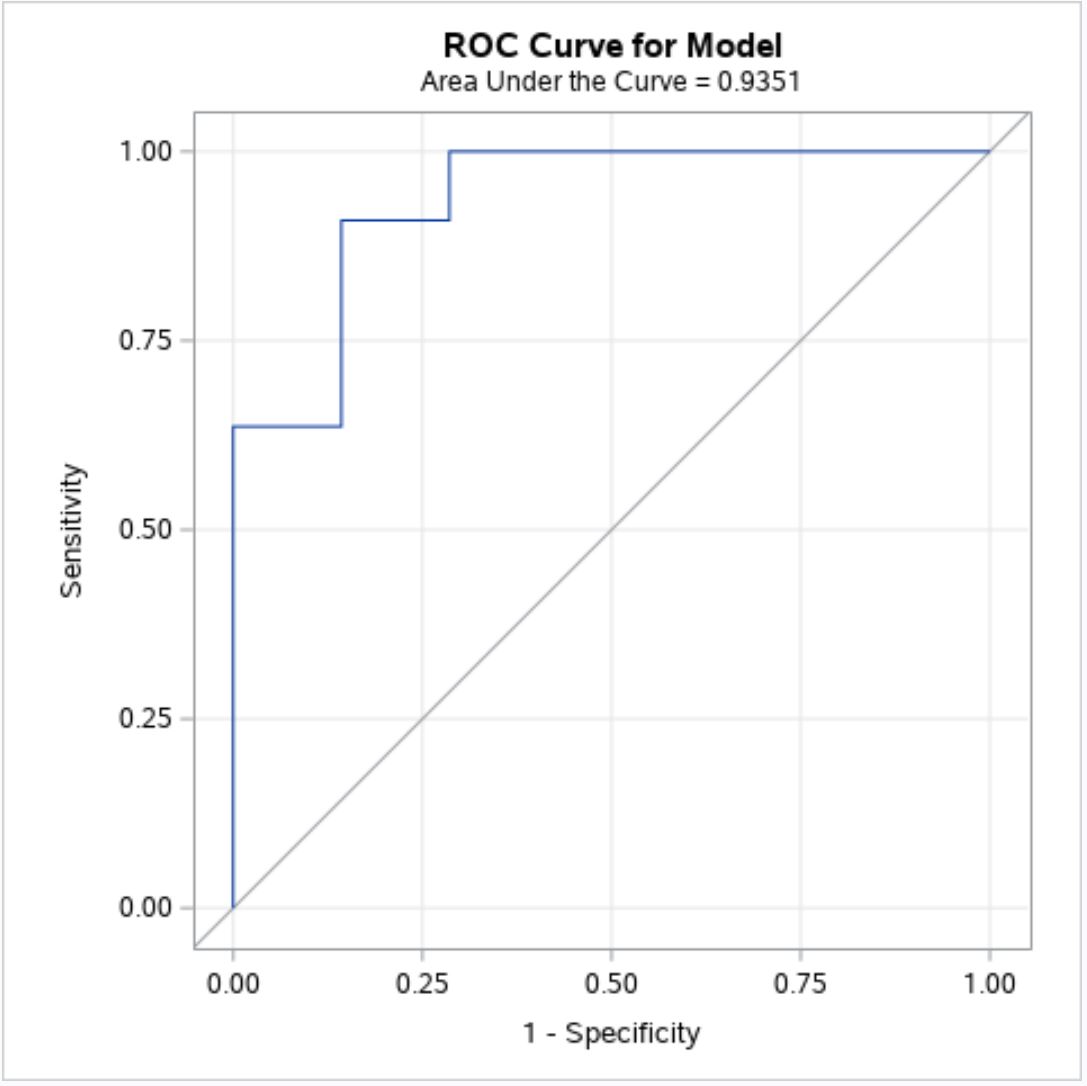
Schritt 3: Interpretieren Sie die ROC-Kurve

Je näher die ROC-Kurve an die obere linke Ecke des Diagramms passt, desto besser sagt das Modell den Wert der Antwortwerte im Datensatz voraus.

Aus der obigen Grafik können wir erkennen, dass die blaue ROC-Kurve dazu neigt, die obere linke Ecke zu umschließen, was darauf hindeutet, dass das logistische Regressionsmodell den Wert der Antwortwerte gut vorhersagen kann.

Um zu quantifizieren, wie gut das logistische Regressionsmodell zu den Daten passt, können wir die AUC (Fläche unter der Kurve) berechnen, die uns sagt, wie viel vom Diagramm unter der Kurve liegt.

Je näher die AUC bei 1 liegt, desto besser ist das Modell. Ein Modell mit einer AUC von 0,5 ist nicht besser als ein Modell, das zufällige Klassifizierungen durchführt.

Unter dem Diagrammtitel oben können wir sehen, dass die AUC dieses Modells 0,9351 beträgt.

Da dieser Wert nahe bei eins liegt, bestätigt dies, dass das Modell den Wert der Antwortwerte gut vorhersagt.

Wir können den AUC-Wert auch verwenden, um die Anpassung verschiedener logistischer Regressionsmodelle zu vergleichen.

Angenommen, wir passen zwei verschiedene logistische Regressionsmodelle an und berechnen jeweils die AUC-Werte:

• AUC von Modell 1: 0,9351
• AUC von Modell 2: 0,8140

Da die AUC von Modell 1 größer ist, bedeutet dies, dass Modell 1 die Daten besser anpassen kann als Modell 2.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige Vorgänge in SAS ausführen:

So führen Sie eine einfache lineare Regression in SAS durch
So führen Sie eine multiple lineare Regression in SAS durch
So führen Sie eine logistische Regression in SAS durch