Halbinterquartilbereich

In diesem Artikel wird erklärt, was der Semi-Interquartilbereich in der Statistik ist. Sie finden also eine Anleitung zur Berechnung des Semi-Interquartil-Bereichs, eine gelöste Übung und zusätzlich einen Online-Rechner zur Berechnung des Semi-Interquartil-Bereichs einer beliebigen Datenstichprobe.

Was ist der Semi-Interquartil-Bereich?

Der Semi-Interquartil-Bereich (oder Semi-Interquartil-Bereich ) beträgt die Hälfte der Differenz zwischen dem ersten und dritten Quartil. Um den Halbquartilbereich zu berechnen, müssen Sie daher das dritte Quartil minus das erste Quartil subtrahieren und dann durch zwei dividieren.

Der Semi-Interquartil-Bereich ist ein Maß für die Streuung, das die Variabilität zentraler Werte angibt. Je größer also der Halbquartilbereich eines Datensatzes ist, desto stärker streuen die Werte in der Mitte relativ zueinander.

Eines der Merkmale des Semi-Interquartil-Bereichs besteht darin, dass es sich um einen robusten statistischen Parameter handelt, sodass Ausreißer keinen Einfluss auf den Semi-Interquartil-Bereich haben.

Somit ist das Semi-Interquartil-Intervall ein dem statistischen Intervall ähnliches Maß für die Streuung, da es die Variabilität eines Datensatzes durch Subtraktion zweier Quartilwerte angibt. Allerdings wird die statistische Reichweite etwas anders berechnet.

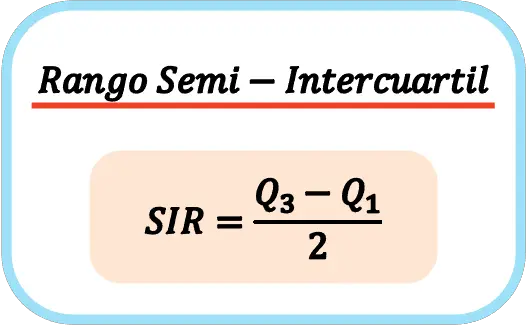
Halbinterquartilbereichsformel

Der Halbquartilbereich entspricht der Differenz zwischen dem dritten Quartil und dem ersten Quartil dividiert durch zwei. Um den Halbquartilbereich zu berechnen, müssen Sie daher zunächst das erste und dritte Quartil ermitteln, diese dann subtrahieren und schließlich das Subtraktionsergebnis durch zwei dividieren.

Die Formel zur Berechnung des Semi-Interquartilbereichs lautet also:

👉 Mit dem Rechner unten können Sie den Halbquartilbereich eines beliebigen Datensatzes berechnen.

Im Allgemeinen wird zur Darstellung des Semi-Interquartil-Bereichs das Akronym SIR ( Semi-Intquartil-Bereich ) als Symbol für dieses statistische Maß verwendet.

Kurz gesagt, der Semi-Interquartil-Bereich beträgt die Hälfte des Interquartil-Bereichs .

Beispiel für die Berechnung des Semi-Interquartil-Bereichs

Nachdem Sie die Definition des Semi-Interquartil-Bereichs und seine Formel kennengelernt haben, finden Sie unten ein konkretes Beispiel, um anschaulich zu erklären, wie der Semi-Interquartil-Bereich berechnet wird.

• Wir wollen statistisch analysieren, ob es sinnvoll ist, in ein Unternehmen zu investieren. Dazu haben wir Daten zum Aktienkurs dieses Unternehmens in den letzten 15 Monaten gesammelt. In der folgenden Tabelle sehen Sie die beobachteten Daten, sortiert vom niedrigsten zum höchsten Wert. Berechnen Sie den Semi-Interquartil-Bereich dieses Datensatzes.

Wie im obigen Abschnitt erläutert, müssen wir zum Ermitteln des Halbquartilbereichs zunächst das erste und dritte Quartil bestimmen.

Das erste Quartil ist der Median der ersten Hälfte der Werte, was dem Wert 8,95 €/Aktie entspricht.

Das dritte Quartil hingegen ist der Zwischenwert der zweiten Hälfte der Werte, also 9,83 €/Aktie.

Sobald wir die Werte des ersten und dritten Quartils kennen, wenden wir einfach die Formel für das Halbquartilintervall an, um seinen Wert zu ermitteln:

Rechner für den Semi-Interquartilbereich

Geben Sie einen statistischen Datensatz in den folgenden Online-Rechner ein, um seinen Halbquartilbereich zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.