So schätzen sie die standardabweichung eines beliebigen histogramms ein

Ein Histogramm bietet eine nützliche Möglichkeit, die Verteilung von Werten in einem Datensatz zu visualisieren.

Die x-Achse eines Histogramms zeigt Gruppen von Datenwerten an und die y-Achse sagt uns, wie viele Beobachtungen in einem Datensatz sich in jeder Gruppe befinden.

Da ein Histogramm Beobachtungen in Klassen einordnet, ist es nicht möglich, die genaue Standardabweichung des durch das Histogramm dargestellten Datensatzes zu berechnen, aber es ist möglich, die Standardabweichung zu schätzen.

Das folgende Beispiel zeigt, wie das geht.

Verwandte Themen: So schätzen Sie den Mittelwert und den Median eines beliebigen Histogramms

So schätzen Sie die Standardabweichung eines Histogramms ein

Um die Standardabweichung eines Histogramms abzuschätzen, müssen Sie zunächst den Mittelwert schätzen.

Wir können die folgende Formel verwenden, um den Durchschnitt zu schätzen:

Durchschnitt: Σm _i n _i / N

Gold:

• m _i : Die Mitte des i- ^ten Behälters
• n _i : Die Häufigkeit des i ^-ten Bins
• N: Die Gesamtstichprobengröße

Angenommen, wir haben das folgende Histogramm:

So schätzen Sie den Durchschnittswert dieses Histogramms:

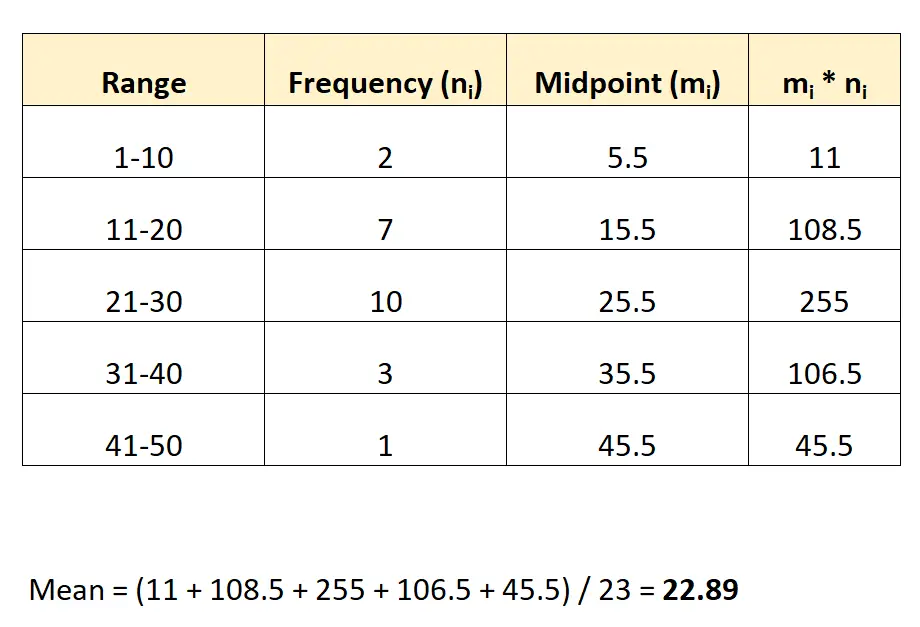
Wir schätzen den Durchschnitt auf 22,89 .

Hinweis: Der Mittelpunkt jeder Gruppe kann durch Bildung des Durchschnitts der unteren und oberen Werte des Bereichs ermittelt werden. Der Mittelpunkt der ersten Gruppe wird beispielsweise wie folgt berechnet: (1+10) / 2 = 5,5.

Nachdem wir nun eine Schätzung des Mittelwerts haben, können wir die folgende Formel verwenden, um die Standardabweichung zu schätzen:

Standardabweichung: √ Σn _i (m _i -μ) ² / (N-1)

Gold:

• n _i : Die Häufigkeit des i ^-ten Bins
• m _i : Die Mitte des i- ^ten Behälters
• μ : Der Durchschnitt
• N: Die Gesamtstichprobengröße

So würden wir diese Formel auf unseren Datensatz anwenden:

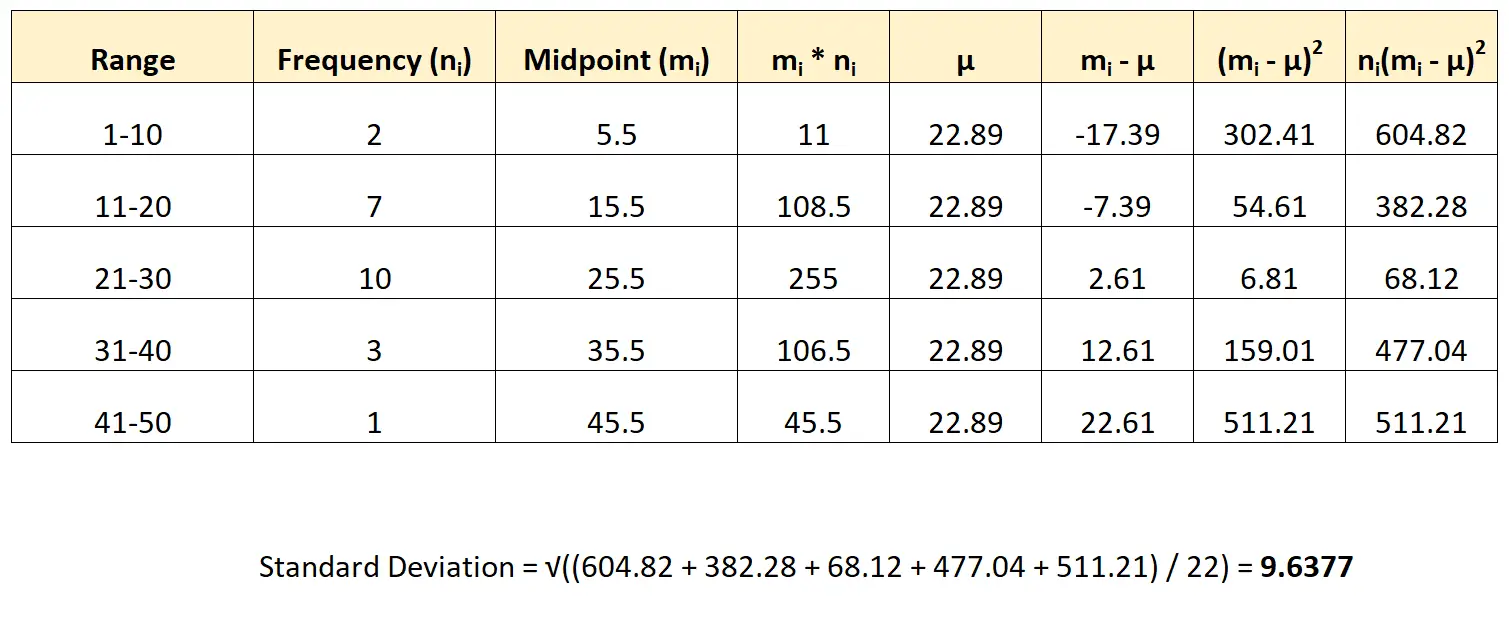Wir schätzen die Standardabweichung des Datensatzes auf 9,6377 .

Obwohl nicht garantiert werden kann, dass es genau mit der Standardabweichung des Datensatzes übereinstimmt (da wir die Rohdatenwerte des Datensatzes nicht kennen), stellt es unsere beste Schätzung der Standardabweichung dar.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben im Zusammenhang mit in Gruppen gruppierten Daten ausführen:

So ermitteln Sie die Varianz gruppierter Daten
So ermitteln Sie den Median gruppierter Daten
So finden Sie den gruppierten Datenmodus