Untere quadrate

Von Dr. Benjamin Anderson August 2, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erläutert, was die Methode der kleinsten Quadrate in der Statistik ist, was die Methode der kleinsten Quadrate ist und wie ein Regressionsmodell anhand des Kriteriums der kleinsten Quadrate angepasst wird.

Was ist die Methode der kleinsten Quadrate?

Die Methode der kleinsten Quadrate ist eine statistische Methode zur Bestimmung der Gleichung einer Regression. Mit anderen Worten: Die Methode der kleinsten Quadrate ist ein Kriterium, das in einem Regressionsmodell verwendet wird, um den Fehler zu minimieren, der bei der Berechnung der Regressionsgleichung entsteht.

Konkret besteht die Methode der kleinsten Quadrate darin, die Summe der Quadrate der Residuen zu minimieren, oder mit anderen Worten, sie basiert auf der Minimierung der Summe der Quadrate der Differenzen zwischen den vom Regressionsmodell vorhergesagten Werten und den beobachteten Werten . . Im Folgenden werden wir im Detail sehen, wie ein Regressionsmodell anhand des Kriteriums der kleinsten Quadrate angepasst wird.

Das Hauptmerkmal der Methode der kleinsten Quadrate besteht darin, dass die längsten Abstände zwischen den beobachteten Werten und der Regressionsfunktion minimiert werden. Im Gegensatz zu anderen Regressionskriterien ist es bei der Methode der kleinsten Quadrate wichtiger, große Residuen zu minimieren als kleine Residuen, da das Quadrat einer großen Zahl viel größer ist als das Quadrat einer kleinen Zahl. Nummer.

Schätzfehler

Um das Konzept der kleinsten Quadrate vollständig zu verstehen, müssen wir uns zunächst darüber im Klaren sein, was Residuen in einem Regressionsmodell sind. Wir werden daher im Folgenden sehen, was ein Schätzfehler ist und wie er berechnet wird.

In der Statistik ist der Schätzfehler , auch Residuum genannt, die Differenz zwischen dem wahren Wert und dem durch das Regressionsmodell angepassten Wert. Ein statistisches Residuum wird daher wie folgt berechnet:

$e_i=y_i-\widehat{y}_i$

Gold:

$e_i$

ist der Rest der Daten i.
$y_i$

ist der wahre Wert der Daten i.
$\widehat{y}_i$

ist der Wert, der vom Regressionsmodell für Daten i bereitgestellt wird.

Je größer also das Residuum eines Datenstücks ist, desto schlechter ist das Regressionsmodell an dieses Datenstück angepasst. Je kleiner also ein Residuum ist, desto geringer ist der Abstand zwischen seinem tatsächlichen Wert und seinem vorhergesagten Wert.

Wenn das Residuum eines Datenelements ebenfalls positiv ist, bedeutet dies, dass das Regressionsmodell einen Wert vorhersagt, der unter dem wahren Wert liegt. Wenn das Residuum hingegen negativ ist, bedeutet dies, dass der vorhergesagte Wert größer als der tatsächliche Wert ist.

Fehlerquadrate minimieren

Da wir nun wissen, was ein Residuum in der Statistik ist, wird es einfacher zu verstehen, wie Fehlerquadrate minimiert werden.

Das Quadrat eines Fehlers ist das Quadrat eines Residuums. Das Quadrat eines Fehlers entspricht also der Differenz zwischen dem wahren Wert und dem durch das Regressionsmodell angepassten Wert, hochgerechnet auf die Zweierpotenz.

$e_i^2=(y_i-\widehat{y}_i)^2$

Gold:

$e_i^2$

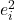
ist das Quadrat des Residuums der Daten i.
$y_i$

ist der wahre Wert der Daten i.
$\widehat{y}_i$

ist der Wert, der vom Regressionsmodell für Daten i bereitgestellt wird.

Somit besteht die Methode der kleinsten Quadrate darin, ein Regressionsmodell zu erstellen , indem die Summe der Fehlerquadrate minimiert wird . Das Kriterium der kleinsten Quadrate basiert daher auf der Minimierung des folgenden Ausdrucks:

$\begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}$

Aus diesem Grund wird das Kriterium der kleinsten Quadrate auch als Kriterium der kleinsten Quadrate bezeichnet.

Wie Sie in der vorherigen Formel sehen können, legt das Kriterium der kleinsten Quadrate mehr Wert auf die Minimierung großer Residuen als auf die Minimierung kleiner Residuen. Wenn beispielsweise ein Rest 3 und ein anderer Rest 5 ist, sind ihre Quadrate 9 bzw. 25, sodass das Kriterium der kleinsten Quadrate der Minimierung des zweiten Rests Vorrang vor dem ersten Rest einräumt.

Anpassung der kleinsten Quadrate

Die Anpassung eines Regressionsmodells mithilfe des Kriteriums der kleinsten Quadrate besteht darin, ein Regressionsmodell zu finden, das die Quadrate der Residuen minimiert. Daher ist die aus dem Regressionsmodell erhaltene Gleichung eine Gleichung, deren Quadrate der Differenzen zwischen den beobachteten Werten und den angepassten Werten minimal sind.

Beachten Sie im folgenden Beispiel, dass es mehr Kriterien für die Erstellung eines Regressionsmodells gibt und je nach gewähltem Kriterium die Regressionsgleichung unterschiedlich ist.

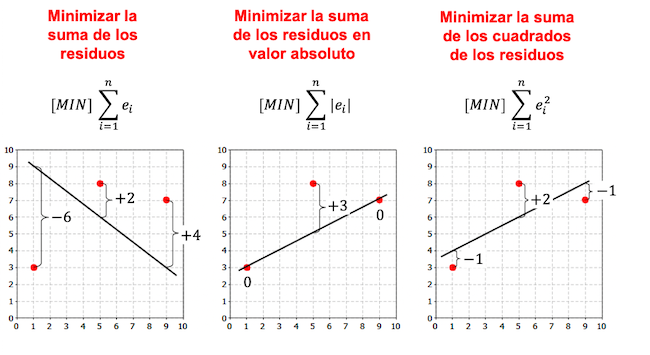
Methode der kleinsten Quadrate, Anpassung der kleinsten Quadrate

Wie Sie in den vorherigen Beispielen sehen können, hängt die aus dem linearen Regressionsmodell für denselben Datensatz erhaltene Linie vom gewählten Kriterium ab. Im Allgemeinen wird in Regressionsmodellen das Kriterium der kleinsten Quadrate verwendet.

Das in der Statistik am weitesten verbreitete Regressionsmodell ist das einfache lineare Regressionsmodell, das darin besteht, die Beziehung zwischen der unabhängigen Variablen X und der abhängigen Variablen Y mithilfe einer Geraden zu approximieren.

$y=b_0+b_1x$

Die Formeln zum Anpassen eines Datensatzes an ein einfaches lineares Regressionsmodell lauten also:

$b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}$

$b_0=\overline{y}-b_1\overline{x}$

Ein Beispiel dafür, wie ein einfaches lineares Regressionsmodell mithilfe des Kriteriums der kleinsten Quadrate berechnet wird, können Sie sehen, indem Sie auf den folgenden Link klicken:

➤ Siehe: Beispiel einer einfachen linearen Regression

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen