Qualität der passform
In diesem Artikel wird erklärt, was die Güte der Anpassung in der Statistik ist. Ebenso wird gezeigt, wie die Anpassungsgüte eines Regressionsmodells gemessen wird, und außerdem können Sie eine gelöste Anpassungsübung sehen.
Was ist die Güte der Passform?
In der Statistik gibt die Anpassungsgüte an, wie gut ein Regressionsmodell zur Datenstichprobe passt. Mit anderen Worten: Die Anpassungsgüte eines Regressionsmodells bezieht sich auf den Grad der Kopplung zwischen der Menge der Beobachtungen und den durch die Regression erhaltenen Werten.
Je besser die Anpassungsgüte eines Regressionsmodells ist, desto besser erklärt es die untersuchten Daten. Wir wollen also, dass das statistische Modell umso besser passt, je besser es passt.
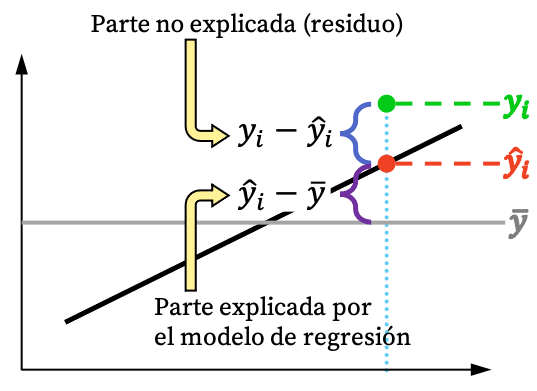
Wie Sie dem Bild oben entnehmen können, kann der Wert einer Beobachtung normalerweise nicht vollständig durch das Regressionsmodell erklärt werden. Aber logischerweise passt das Modell umso besser, je mehr das Regressionsmodell anhand des Datensatzes erklären kann. Kurz gesagt, wir sind an einem möglichst engen Regressionsmodell interessiert.
Anpassungsgüte eines Regressionsmodells
Um die Anpassungsgüte eines Regressionsmodells zu bestimmen, verwendet man typischerweise das Bestimmtheitsmaß , einen statistischen Koeffizienten, der den durch das Regressionsmodell erklärten Prozentsatz angibt. Je höher also das Bestimmtheitsmaß eines Modells ist, desto besser passt sich das Modell an die Datenstichprobe an.
![]()
Allerdings ist zu beachten, dass das Bestimmtheitsmaß eines Regressionsmodells umso höher ist, je mehr Variablen es hat. Aus diesem Grund wird das angepasste Bestimmtheitsmaß auch häufig zur Messung der Anpassungsgüte eines Modells verwendet. Der angepasste Bestimmtheitskoeffizient ist eine Variation des vorherigen Koeffizienten, der den durch das Regressionsmodell erklärten Prozentsatz angibt und jede im Modell enthaltene erklärende Variable benachteiligt.
![]()
Daher ist es vorzuziehen, das angepasste Bestimmtheitsmaß zum Vergleich zweier Modelle mit mehreren unterschiedlichen Variablen zu verwenden, da es die Anzahl der im Modell enthaltenen Variablen berücksichtigt.
Abschließend ist zu beachten, dass der Chi-Quadrat-Test auch zur Messung der Anpassungsgüte eines Regressionsmodells verwendet werden kann, obwohl üblicherweise die Werte der beiden vorherigen Koeffizienten verwendet werden.
Konkretes Beispiel für gute Passform
Abschließend werden wir eine detaillierte Übung zur Qualität der Anpassung sehen, um die Assimilation dieses statistischen Konzepts abzuschließen.
- Mit derselben Datenreihe werden zwei unterschiedliche lineare Regressionsmodelle durchgeführt, deren Ergebnisse Sie in der folgenden Tabelle sehen können. Welches Modell eignet sich am besten?
| Regressionsmodell 1 | Regressionsmodell 2 | |
|---|---|---|
| Bestimmtheitsmaß | 57 % | 64 % |
| Angepasster Bestimmungskoeffizient | 49 % | 43 % |
| Anzahl erklärender Variablen | 3 | 7 |
In diesem Fall gehen wir davon aus, dass beide Modelle die vorherigen Annahmen linearer Regressionsmodelle erfüllen und wir daher nur die Anpassungsgüte der Modelle analysieren müssen.
Regressionsmodell 2 hat ein höheres Bestimmtheitsmaß als Regressionsmodell 1 und scheint daher a priori ein besseres Regressionsmodell zu sein, da es die Datenstichprobe besser erklären kann.
Allerdings verfügt das Regressionsmodell 2 über 7 unabhängige Variablen im Modell, während das Regressionsmodell 1 nur über 3 verfügt. Daher wird Modell 2 viel komplizierter und schwieriger zu interpretieren sein als das erste Modell.
Wenn wir uns außerdem das angepasste Bestimmtheitsmaß ansehen, das die Anzahl der Variablen im Modell berücksichtigt, weist Regressionsmodell 1 ein höheres angepasstes Bestimmtheitsmaß auf als Regressionsmodell 2.
Zusammenfassend lässt sich sagen, dass es zwar besser ist, Regressionsmodell 1 zu verwenden, da sein angepasster Bestimmtheitskoeffizient höher ist als der von Regressionsmodell 2. Regressionsmodell 2 weist einen höheren unbereinigten Bestimmtheitskoeffizienten auf, dies liegt jedoch daran, dass viel mehr Variablen in die Regression einbezogen wurden Modell 1. Modell, das den Wert des Koeffizienten erhöht, aber die Interpretation des Modells schwieriger macht und sicherlich die Vorhersage eines neuen Werts verschlechtert.
Um Modelle mit einer unterschiedlichen Anzahl von Variablen zu vergleichen, ist es am besten, den angepassten Bestimmtheitskoeffizienten zu verwenden, da dieser für jede dem Modell hinzugefügte Variable einen Nachteil darstellt. Wie Sie in diesem Beispiel gesehen haben, ist das Regressionsmodell 2 gemäß dem nicht angepassten Bestimmtheitsmaß besser. Durch das angepasste Bestimmtheitsmaß können wir jedoch erkennen, dass Regressionsmodell 1 tatsächlich besser ist.