Polynomielle regression

Von Dr. Benjamin Anderson August 2, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was Polynomregression in der Statistik ist und wie sie durchgeführt wird. Darüber hinaus sehen Sie ein Beispiel, in dem eine polynomielle Regression durchgeführt wird.

Was ist polynomielle Regression?

Polynomielle Regression oder Polynomregression ist ein Regressionsmodell, bei dem die Beziehung zwischen der unabhängigen Variablen X und der abhängigen Variablen Y mithilfe eines Polynoms modelliert wird.

Die Gleichung für ein quadratisches Polynom-Regressionsmodell lautet beispielsweise y=β ₀ +β ₁ x+β ₂ x ² +ε.

Die Polynomregression eignet sich zum Anpassen von Datensätzen, deren Diagramme Polynomkurven sind. Wenn also das Punktdiagramm einer Datenstichprobe die Form einer Parabel hat, ist es besser, ein quadratisches Regressionsmodell anstelle eines linearen Regressionsmodells zu erstellen. Auf diese Weise passt die Regressionsmodellgleichung besser zur Datenstichprobe.

Beachten Sie, dass die polynomiale Regression eine Art nichtlineare Regression ist, genau wie die exponentielle Regression und die logarithmische Regression.

Polynomielle Regressionsformel

Die Gleichung für ein polynomiales Regressionsmodell lautet y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε.

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

Gold:

$y$

ist die abhängige Variable.
$x$

ist die unabhängige Variable.
$\beta_0$

ist die Konstante der polynomialen Regressionsgleichung.
$\beta_i$

ist der mit der Variablen verbundene Regressionskoeffizient

$x^i$

.
$\bm{\varepsilon}$

Dabei handelt es sich um den Fehler bzw. Residuum, also um die Differenz zwischen dem beobachteten Wert und dem vom Modell geschätzten Wert.

Wenn wir also eine Stichprobe mit insgesamt haben

$n$

Beobachtungen können wir das polynomiale Regressionsmodell in Matrixform vorschlagen:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

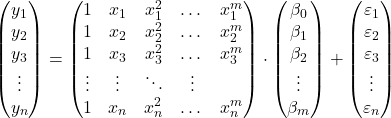
Der obige Matrixausdruck kann umgeschrieben werden, indem jeder Matrix ein Buchstabe zugewiesen wird:

$Y=X\beta+\varepsilon$

Durch Anwendung des Kriteriums der kleinsten Quadrate können wir also zu der Formel zur Schätzung der Koeffizienten eines polynomialen Regressionsmodells gelangen:

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

Allerdings ist die manuelle Durchführung dieser Berechnungen sehr mühsam und zeitaufwändig. Daher ist es praktischer, Computersoftware (wie Minitab oder Excel) zu verwenden, mit der Sie ein polynomiales Regressionsmodell viel schneller durchführen können.

Beispiel eines polynomialen Regressionsmodells

Nachdem wir nun die Definition der Polynomregression und ihre Durchführung kennen, schauen wir uns ein Beispiel aus der Praxis an, um das Konzept vollständig zu verstehen.

Zunächst ist zu bedenken, dass ein polynomiales Regressionsmodell dann durchgeführt werden sollte, wenn der Datengraph die Form einer polynomialen Kurve hat. Wenn das Punktdiagramm beispielsweise die Form einer kubischen Kurve hat, müssen wir ein polynomiales Regressionsmodell dritten Grades erstellen.

Wie Sie im folgenden Bild sehen können, hat das Punktdiagramm unserer Daten eine quadratische Form, da die abhängige Variable schneller wächst, wenn wir den Wert der unabhängigen Variablen erhöhen. In diesem Fall wurde ein lineares Regressionsmodell durchgeführt und wie Sie sehen können, passt es nicht gut zu den Punkten, da es Abschnitte hat, in denen die Linie unter allen Punkten liegt, und Abschnitte, in denen die Linie über ihnen liegt.

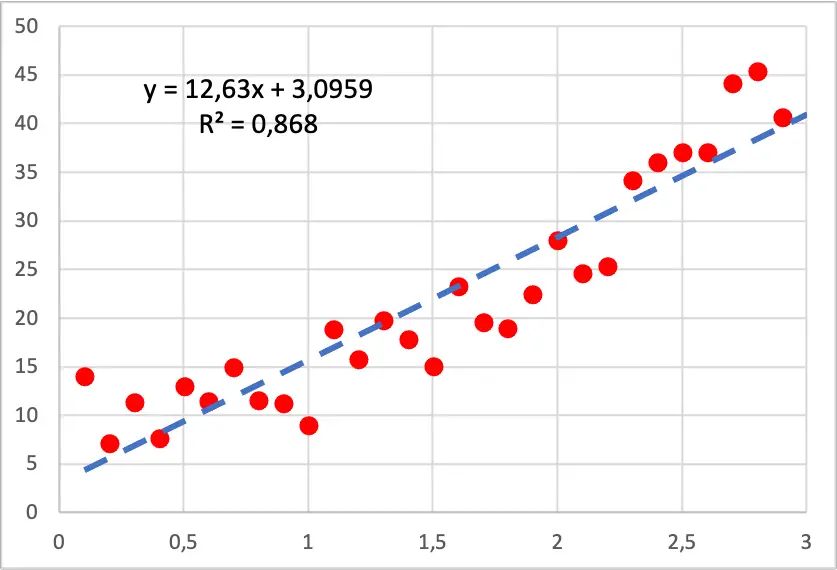
Wenn wir hingegen ein quadratisches Polynom-Regressionsmodell ausführen, passt es viel besser zu den Beispieldaten, wie Sie im Bild unten sehen können.

Beispiel für eine polynomielle Regression

Darüber hinaus verbessert sich bei der Entwicklung eines polynomialen Regressionsmodells das Bestimmtheitsmaß erheblich, da es von 86,80 % auf 94,05 % steigt. Daher erklärt das neue Regressionsmodell den Datensatz viel besser.

Andererseits ist die Darstellung der Residuen ein weiterer Hinweis darauf, dass wir eine polynomielle Regression durchführen müssen. Wenn in einer linearen Regression der Graph der Residuen die Form einer Parabel oder eines anderen Polynomtyps hat, passt ein polynomiales Regressionsmodell sicherlich besser zu den untersuchten Daten.

Andere Arten der nichtlinearen Regression

Es gibt hauptsächlich drei Arten der nichtlinearen Regression:

Polynomielle Regression – Die Gleichung des Regressionsmodells liegt in Form eines Polynoms vor.
Logarithmische Regression : Der Logarithmus der unabhängigen Variablen wird genommen.
Exponentielle Regression : Die unabhängige Variable wird im Exponenten der Gleichung gefunden.

➤ Siehe: Logarithmische Regression
➤ Siehe: Exponentielle Regression

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen