So führen sie eine loess-regression in r durch (mit beispiel)

Die LOESS-Regression , manchmal auch lokale Regression genannt, ist eine Methode, die lokale Anpassungen verwendet, um ein Regressionsmodell an einen Datensatz anzupassen.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie eine LOESS-Regression in R durchgeführt wird.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst den folgenden Datenrahmen in R:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
                 y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))

#view first six rows of data frame
head(df)

  xy
1 1 1
2 2 4
3 3 7
4 4 13
5 5 19
6 6 24

Schritt 2: Passen Sie mehrere LOESS-Regressionsmodelle an

Wir können die Funktion loess() verwenden, um mehrere LOESS-Regressionsmodelle an diesen Datensatz anzupassen, indem wir unterschiedliche Werte für den Span- Parameter verwenden:

 #fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50) 

loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75) 

loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90) 

#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
        col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')

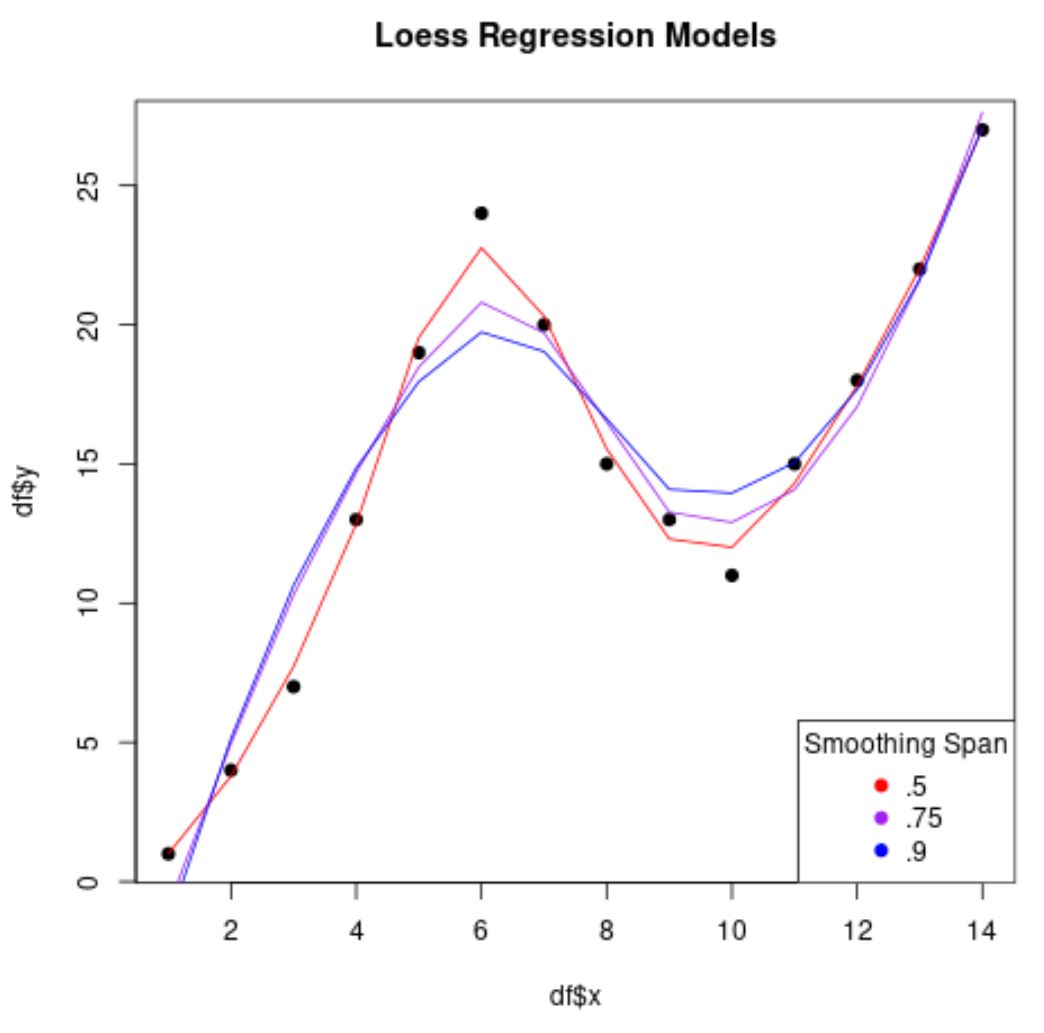
Beachten Sie, dass das Regressionsmodell umso weniger „glatt“ ist und umso mehr versucht, die Datenpunkte anzupassen, je niedriger der Wert ist, den wir für span verwenden.

Schritt 3: Verwenden Sie die K-Fold-Kreuzvalidierung, um das beste Modell zu finden

Um den optimalen zu verwendenden Extent- Wert zu finden, können wir mithilfe der Funktionen im Caret- Paket eine k-fache Kreuzvalidierung durchführen:

 library (caret)

#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )

#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)

#print results of k-fold cross-validation
print (model)

14 samples
 1 predictor

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 12, 11, 11, 11, 11 
Resampling results across tuning parameters:

  span RMSE Rsquared MAE      
  0.5 10.148315 0.9570137 6.467066
  0.6 7.854113 0.9350278 5.343473
  0.7 6.113610 0.8150066 4.769545
  0.8 17.814105 0.8202561 11.875943
  0.9 26.705626 0.7384931 17.304833

Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.

Wir können sehen, dass der Spannenwert , der den niedrigsten Wert für den quadratischen Mittelfehler (RMSE) ergab, 0,7 beträgt.

Daher würden wir für unser endgültiges LOESS-Regressionsmodell einen Wert von 0,7 für das Span- Argument in der Funktion loess() verwenden.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Regressionsmodellen in R:

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine logistische Regression in R durch
So führen Sie eine Quantilregression in R durch
So führen Sie eine gewichtete Regression in R durch