Der unterschied zwischen z-werten und p-werten in der statistik

Zwei Begriffe, die Studierende in der Statistik häufig verwechseln, sind Z-Werte und P-Werte .

Um den Unterschied zwischen diesen Begriffen zu verstehen, ist es hilfreich, Z-Tests zu verstehen.

Es gibt zwei gängige Arten von Z-Tests:

• Z-Test bei einer Stichprobe : Wird verwendet, um zu testen, ob ein Populationsmittelwert einem bestimmten Wert entspricht.
• Z-Test bei zwei Stichproben : Wird verwendet, um zu testen, ob zwei Populationsmittelwerte gleich sind.

Wir verwenden die folgenden Schritte, um jeden Test durchzuführen:

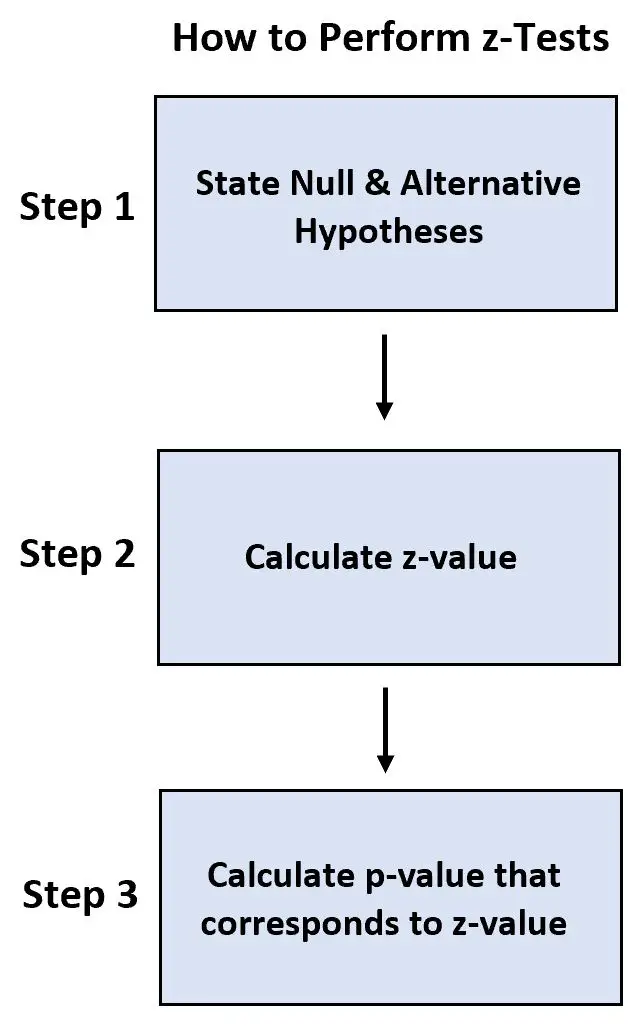
• Schritt 1: Geben Sie die Null- und Alternativhypothese an.
• Schritt 2: Berechnen Sie den Z-Wert.
• Schritt 3: Berechnen Sie den p-Wert, der dem z-Wert entspricht.

Für jeden Test ist der Z-Wert eine Möglichkeit, die Differenz zwischen den Mittelwerten der Grundgesamtheit zu quantifizieren, und der P-Wert ist die Wahrscheinlichkeit, einen Z-Wert mit einem Absolutwert zu erhalten, der mindestens so groß ist, wie wir ihn tatsächlich in der Stichprobe beobachtet haben. Daten, wenn die Nullhypothese tatsächlich wahr ist.

Wenn der p-Wert kleiner als ein bestimmter Wert ist (z. B. 0,05), lehnen wir die Nullhypothese des Tests ab.

Für jede Art von Z-Test interessiert uns der p-Wert und wir verwenden den z-Wert einfach als Zwischenschritt zur Berechnung des p-Werts.

Das folgende Beispiel zeigt, wie ein Z-Wert und der entsprechende p-Wert für einen Z-Test mit zwei Stichproben berechnet und interpretiert werden.

Beispiel: Z-Werte und P-Werte berechnen und interpretieren

Gehen Sie davon aus, dass die IQ-Werte von Personen aus zwei verschiedenen Städten normalverteilt sind und jeweils eine Bevölkerungsstandardabweichung von 15 aufweisen.

Ein Wissenschaftler möchte wissen, ob der durchschnittliche IQ-Wert zwischen Personen in Stadt A und Stadt B unterschiedlich ist. Sie wählt daher eine einfache Zufallsstichprobe von 20 Personen aus jeder Stadt aus und erfasst deren IQ-Werte:

Stadt A : 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114

Stadt B : 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133

So führen Sie mit diesen Daten einen Z-Test bei zwei Stichproben durch:

Schritt 1: Geben Sie die Null- und Alternativhypothese an.

Zunächst stellen wir die Null- und Alternativhypothese auf:

• H ₀ : μ ₁ = μ ₂ (die beiden Populationsmittelwerte sind gleich)
• H ₁ : μ ₁ ≠ μ ₂ (die beiden Populationsmittelwerte sind nicht gleich)

Schritt 2: Berechnen Sie den Z-Wert.

Als Nächstes führen wir mit diesen Daten einen Z-Test bei zwei Stichproben in Excel durch und stellen fest, dass der Z-Wert -1,71817 beträgt.

Schritt 3: Berechnen Sie den p-Wert.

Wir können den Z-Score-zu-P-Wert-Rechner verwenden, um herauszufinden, dass der p-Wert, der einem z-Wert von -1,71817 entspricht, 0,08577 beträgt.

Da dieser p-Wert nicht weniger als 0,05 beträgt, verfügen wir nicht über ausreichende Beweise, um die Nullhypothese abzulehnen.

Wir kommen daher zu dem Schluss, dass sich das durchschnittliche IQ-Niveau zwischen den beiden Städten nicht wesentlich unterscheidet.

Beachten Sie, dass wir einfach den z-Wert als Zwischenschritt zur Berechnung des p-Werts verwendet haben.

Der p-Wert ist der wahre Wert, an dem wir interessiert waren, aber wir mussten zuerst den z-Wert berechnen.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie Z-Tests mit verschiedenen Statistiksoftware durchführen:

So führen Sie Z-Tests in Excel durch
So führen Sie Z-Tests in R durch
So führen Sie Z-Tests in Python durch