So lesen sie einen boxplot mit ausreißern (mit beispiel)

Ein Boxplot ist eine Art Diagramm, das die fünfstellige Zusammenfassung eines Datensatzes anzeigt, der Folgendes umfasst:

• Der Mindestwert
• Das erste Quartil (das 25. Perzentil)
• Der Medianwert
• Das dritte Quartil (das 75. Perzentil)
• Der Maximalwert

Um ein Boxplot zu erstellen, zeichnen wir zunächst eine Box vom ersten bis zum dritten Quartil.

Als nächstes zeichnen wir eine vertikale Linie am Mittelwert.

Abschließend zeichnen wir „Whisker“ der Quartile bis zum Minimal- und Maximalwert.

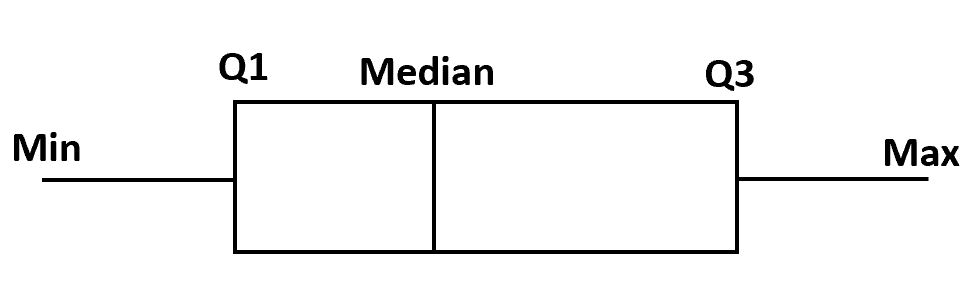
In den meisten Statistikprogrammen wird eine Beobachtung als Ausreißer definiert, wenn sie eine der folgenden beiden Anforderungen erfüllt:

• Die Beobachtung beträgt das 1,5-fache des Interquartilbereichs unterhalb des ersten Quartils (Q1).
• Die Beobachtung beträgt das 1,5-fache des Interquartilbereichs über dem dritten Quartil (Q3).

Wenn in einem Datensatz ein Ausreißer vorhanden ist, wird dieser im Boxplot normalerweise mit einem kleinen Punkt außerhalb des Whisker-Bereichs gekennzeichnet:

In diesem Fall werden den „minimalen“ und „maximalen“ Werten im Boxplot einfach die Werte Q1 – 1,5*IQR bzw. Q3 + 1,5*IQR zugewiesen.

Das folgende Beispiel zeigt, wie Boxplots mit und ohne Ausreißer interpretiert werden.

Beispiel: Interpretation eines Boxplots mit Ausreißern

Angenommen, wir erstellen die folgenden zwei Boxplots, um die Verteilung der von Basketballspielern aus zwei verschiedenen Teams erzielten Punkte zu visualisieren:

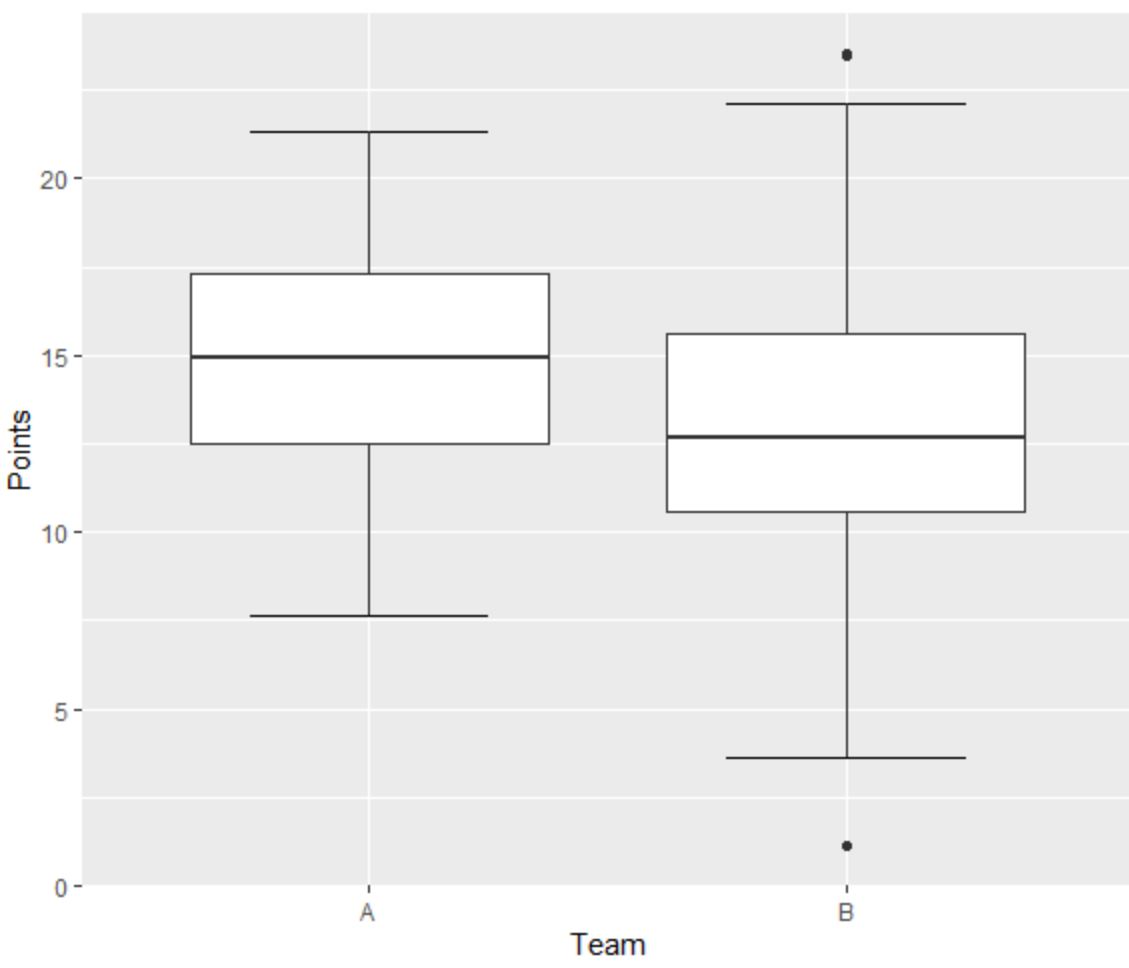
Das linke Boxplot für Team A weist keine Ausreißer auf, da sich außerhalb des minimalen oder maximalen Whiskers keine kleinen Punkte befinden.

Das rechte Boxplot für Team B weist jedoch einen Ausreißer über dem „Maximum“-Wert und einen Ausreißer unter dem „Minimal“-Wert auf.

Hier ist die aktuelle fünfstellige Zusammenfassung zur Verteilung der Variable „Punkte“ für Team B:

• Mindestwert: 1,1
• Erstes Quartil: 10,5
• Median: 12,7
• Drittes Quartil: 15,6
• Maximalwert: 23,5

So berechnen Sie die Grenzen potenzieller Ausreißer:

Interquartilskala : Drittes Quartil – Erstes Quartil = 15,6 – 10,5 = 5,1

Untere Grenze : Q1 – 1,5*IQR = 10,5 – 1,5*5,1 = 2,85

Obergrenze : Q3 + 1,5*IQR = 15,6 + 1,5*5,1 = 23,25

Die Whiskers für die Minimal- und Maximalwerte im Boxplot liegen bei 2,85 und 23,25 .

Daher gelten Beobachtungen mit Werten von 1,1 und 23,5 beide als Ausreißer im Boxplot, da sie außerhalb der unteren und oberen Grenzen liegen.

Bonus : Hier ist der genaue Code, den wir zum Erstellen dieser beiden Boxplots in der Programmiersprache R verwendet haben:

 library (ggplot2)

#make this example reproducible 
set. seeds (2)

#create data frame
df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), 
                 Points = c(rnorm(200, mean = 15, sd = 3), 
                           rnorm(200, mean = 12, sd = 4))) 

#create box plots
ggplot(df, aes(x = Team, y = Points)) +
  stat_boxplot(geom = " errorbar ", width = 0.5) +  
  geom_boxplot() 

#calculate summary statistics for each team
tapply(df$Points, df$Team, summary)

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Boxplots:

So vergleichen Sie Boxplots
So identifizieren Sie Asymmetrie in Boxplots
So ermitteln Sie den Interquartilbereich eines Boxplots