Bedingte wahrscheinlichkeit (oder bedingte wahrscheinlichkeit)

Hier erfahren Sie, was eine bedingte Wahrscheinlichkeit (bzw. bedingte Wahrscheinlichkeit) ist. Wir erklären anhand eines Beispiels, wie die bedingte Wahrscheinlichkeit berechnet wird und welche Eigenschaften diese Art von Wahrscheinlichkeit hat. Darüber hinaus können Sie Schritt für Schritt gelöste bedingte Wahrscheinlichkeitsübungen üben.

Was ist bedingte Wahrscheinlichkeit?

Die bedingte Wahrscheinlichkeit , auch bedingte Wahrscheinlichkeit genannt, ist ein statistisches Maß, das die Wahrscheinlichkeit angibt, dass Ereignis A eintritt, wenn ein anderes Ereignis B eintritt. Das heißt, die bedingte Wahrscheinlichkeit P(A|B) bezieht sich auf die Wahrscheinlichkeit, dass Ereignis A eintritt, nachdem Ereignis B bereits eingetreten ist.

Die bedingte Wahrscheinlichkeit wird mit einem vertikalen Balken zwischen den beiden Ereignissen geschrieben: P(A|B) und lautet: „die bedingte Wahrscheinlichkeit von Ereignis A bei gegebenem Ereignis B“.

Beachten Sie, dass der bedingte Wahrscheinlichkeitswert eine Zahl zwischen 0 und 1 ist. Je höher die bedingte Wahrscheinlichkeit, desto wahrscheinlicher ist es, dass Ereignis A eintritt, wenn Ereignis B eintritt. Je niedriger die bedingte Wahrscheinlichkeit, desto unwahrscheinlicher ist es jedoch, dass Ereignis A eintritt wird eintreten, wenn Ereignis B eintritt.

Bedingte Wahrscheinlichkeitsformel

Die bedingte Wahrscheinlichkeit von Ereignis A bei gegebenem Ereignis B ist gleich der Wahrscheinlichkeit des Schnittpunkts zwischen Ereignis A und Ereignis B dividiert durch die Wahrscheinlichkeit von Ereignis B.

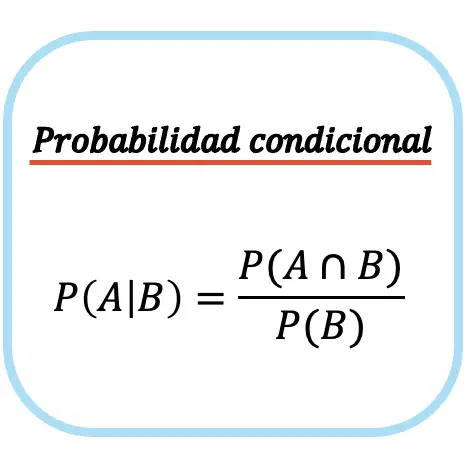
Beachten Sie, dass die Formel für die bedingte Wahrscheinlichkeit (oder bedingte Wahrscheinlichkeit) nur verwendet werden kann, wenn die Eintrittswahrscheinlichkeit des unbedingten Ereignisses ungleich Null ist, dh P(B)≠0. Oder mit anderen Worten, ob das Eintreten von Ereignis B möglich ist.

Die bedingte Wahrscheinlichkeit kann auch aus ihrer Umkehrung berechnet werden, dh wenn P(B|A) bekannt ist, kann P(A|B) bestimmt werden. Aber dazu müssen Sie den Satz von Bayes anwenden. Woraus dieser Satz besteht, können Sie hier sehen:

Beispiel für bedingte Wahrscheinlichkeit

Sobald wir die Definition und Formel der bedingten Wahrscheinlichkeit gesehen haben, werden wir Schritt für Schritt ein Beispiel dieser Art von Wahrscheinlichkeit lösen, um ihre Bedeutung vollständig zu verstehen.

• Nachdem eine Klasse mit 30 Schülern eine Prüfung abgelegt hatte, wurden Daten gesammelt, um herauszufinden, wie viele Schüler lernten und wie viele bestanden. Die Ergebnisse sind in der folgenden Kontingenztabelle dargestellt. Berechnen Sie aus den gesammelten Daten die bedingte Wahrscheinlichkeit, eine Prüfung zu bestehen, wenn Sie bereits studiert haben.

Um die bedingte Wahrscheinlichkeit zu erhalten, müssen wir die Formel anwenden, die wir zuvor gesehen haben:

Daher müssen wir zunächst die Wahrscheinlichkeit ermitteln, dass ein Student studiert, studiert und bestanden hat. Um die Wahrscheinlichkeit zu ermitteln, dass ein Student studiert hat, müssen wir lediglich die Laplace-Regel anwenden, das heißt, wir dividieren die Anzahl der Studenten, die studiert haben, durch die Gesamtzahl der Beobachtungen:

Und wir können die Wahrscheinlichkeit, dass ein Student gleichzeitig studiert und bestanden hat, aus der Kontingenztabelle ermitteln, indem wir die Anzahl der Studenten, die studiert und bestanden haben, durch die Gesamtzahl dividieren:

Somit beträgt die Wahrscheinlichkeit, dass ein Student eine Prüfung besteht, wenn er studiert hat:

Bedingte Wahrscheinlichkeit abhängiger und unabhängiger Ereignisse

In diesem Abschnitt werden wir sehen, welche Beziehung zwischen bedingter Wahrscheinlichkeit und abhängigen und unabhängigen Ereignissen (oder abhängigen und unabhängigen Ereignissen) besteht. Denn obwohl es sich um unterschiedliche Konzepte handelt, sind diese beiden Arten von Ereignissen mit einer bedingten Wahrscheinlichkeit verbunden.

Zwei Ereignisse (oder Ereignisse) sind unabhängig, wenn ihre Eintrittswahrscheinlichkeit nicht voneinander abhängt. In einem solchen Fall entspricht der Schnittpunkt zwischen den beiden Ereignissen dem Produkt der Wahrscheinlichkeit jedes einzelnen Ereignisses. Und deshalb wird die bedingte Wahrscheinlichkeitsformel vereinfacht:

Kurz gesagt: Wenn die Ereignisse A und B unabhängig sind, ist die bedingte Wahrscheinlichkeit von Ereignis A bei gegebenem Ereignis B genau gleich der Wahrscheinlichkeit, dass Ereignis A eintritt.

Wenn andererseits zwei Ereignisse voneinander abhängig sind, bedeutet dies, dass die Wahrscheinlichkeit eines Ereignisses von der Wahrscheinlichkeit des anderen Ereignisses abhängt. Wenn also zwei Ereignisse A und B abhängig sind, unterscheidet sich die bedingte Wahrscheinlichkeit von Ereignis A bei gegebenem Ereignis B von der Eintrittswahrscheinlichkeit von Ereignis A.

Übungen zur bedingten Wahrscheinlichkeit gelöst

Übung 1

Wir wissen, dass in einer Tüte voller Kugeln die Hälfte orange und die andere Hälfte grün ist. Darüber hinaus sind ein Drittel aller Bälle orange und gleichzeitig mit einem Schild gekennzeichnet. Wie hoch ist die Wahrscheinlichkeit, dass eine orangefarbene Kugel, wenn Sie sie ziehen, das Signal empfängt?

Um die Aufgabe zu lösen, müssen wir die bedingte Wahrscheinlichkeitsformel anwenden, die lautet:

Die Problemstellung sagt uns, dass die Hälfte der Tüte aus Orangen besteht. Daher beträgt die theoretische Wahrscheinlichkeit, einen orangefarbenen Ball aufzuheben, 50 %.

Andererseits wissen wir, dass ein Drittel der Gesamtmenge aus orangefarbenen Kugeln besteht und ein Signal hat. Die Wahrscheinlichkeit, eine orangefarbene Kugel mit einem Signal zu erhalten, beträgt also:

Schließlich setzen wir die berechneten Wahrscheinlichkeiten in die bedingte Wahrscheinlichkeitsformel ein, um ihren Wert zu ermitteln:

Zusammenfassend beträgt die Wahrscheinlichkeit, eine Kugel mit dem Signal zu ziehen, wenn diese orange ist, 66 %.

Übung 2

Wenn wir sechs blaue Stifte und drei schwarze Stifte in einer Box haben, berechnen Sie die Wahrscheinlichkeit, einen einzelnen blauen Stift zu zeichnen, und die Wahrscheinlichkeit, zwei blaue Stifte nacheinander zu zeichnen.

Um die Wahrscheinlichkeit zu bestimmen, einmal einen blauen Stift in die Hand zu nehmen, verwenden Sie einfach das Laplacesche Gesetz:

Das Problem fordert uns auch auf, die Wahrscheinlichkeit zu kennen, zwei blaue Stifte nacheinander in die Hand zu nehmen, d. h. die bedingte Wahrscheinlichkeit, einen blauen Stift in die Hand zu nehmen, wenn wir bereits zuvor einen blauen Stift in die Hand genommen haben.

Wenn wir einen blauen Stift zeichnen, haben wir einen ungünstigeren Fall, aber insgesamt gibt es auch einen Stift weniger. Die bedingte Wahrscheinlichkeit ist daher:

Übung 3

Wie hoch ist die bedingte Wahrscheinlichkeit, einen Würfel auf die Zahl 4 zu werfen, vorausgesetzt, dass der Münzwurf „Kopf“ ergibt?

Um diese Aufgabe zu lösen, müssen Sie die Theorie der bedingten Wahrscheinlichkeit berücksichtigen, da die Ereignisse „Erreichen der Zahl 4 durch Würfeln“ und „Erreichen von Kopf durch Werfen einer Münze“ unabhängig voneinander sind. Es ist daher nicht notwendig, die bedingte Wahrscheinlichkeitsformel zu verwenden, aber die folgende Gleichheit ist erfüllt:

Um die bedingte Wahrscheinlichkeit zu ermitteln, verwenden Sie einfach die Laplace-Regel:

Übung 4

Untersucht wurde das Geschäftsjahr von 25 Unternehmen eines Landes und wie sich deren Aktienkurse in Abhängigkeit vom wirtschaftlichen Ergebnis des Jahres verändern. Die gesammelten Daten können Sie der folgenden Kontingenztabelle entnehmen:

Wie wahrscheinlich ist es, dass der Aktienkurs eines Unternehmens steigt, wenn es im vergangenen Jahr einen Gewinn erzielt hat?

In der Übung werden wir nach der bedingten Wahrscheinlichkeit gefragt, dass die Aktien steigen, vorausgesetzt, das Unternehmen hat ein positives Wirtschaftsergebnis erzielt. Um diese Wahrscheinlichkeit zu berechnen, müssen wir also die bedingte Wahrscheinlichkeitsformel verwenden:

Wir berechnen daher erstens die Wahrscheinlichkeit, dass ein Unternehmen einen Gewinn erzielt, und zweitens die Wahrscheinlichkeit, dass ein Unternehmen einen wirtschaftlichen Gewinn erzielt und gleichzeitig seinen Preis pro Aktie erhöht:

Und dann setzen wir die gefundenen Werte in die Formel ein und berechnen die bedingte Wahrscheinlichkeit:

Eigenschaften der bedingten Wahrscheinlichkeit

Die Eigenschaften der bedingten Wahrscheinlichkeit oder bedingten Wahrscheinlichkeit sind wie folgt:

• Die Summe der bedingten Wahrscheinlichkeit von Ereignis A bei gegebenem Ereignis B plus der bedingten Wahrscheinlichkeit des komplementären Ereignisses A bei gegebenem Ereignis B ist gleich eins.

• Wenn Ereignis A eine Teilmenge von Ereignis B ist, wird A immer dann eintreten, wenn B wahr ist. Somit beträgt die bedingte Wahrscheinlichkeit von Ereignis A bei gegebenem Ereignis B in diesen Fällen 1.

• Bei zwei unterschiedlichen Ereignissen gilt hinsichtlich der bedingten Wahrscheinlichkeit immer die folgende Gleichheit: