Hypergeometrische verteilung

Von Dr. Benjamin Anderson August 6, 2023 Wahrscheinlichkeit Keine Kommentare

In diesem Artikel erklären wir, was die hypergeometrische Verteilung ist und wie mit dieser Art von Verteilung eine Wahrscheinlichkeit berechnet wird. Sie finden online die Formel für die hypergeometrische Verteilung, ihre Eigenschaften sowie einen Rechner zur Berechnung der Wahrscheinlichkeit der hypergeometrischen Verteilung.

Was ist die hypergeometrische Verteilung?

Die hypergeometrische Verteilung ist eine Wahrscheinlichkeitsverteilung, die die Anzahl erfolgreicher Fälle bei einer zufälligen Extraktion ohne Ersetzung von n Elementen aus einer Grundgesamtheit beschreibt.

Das heißt, die hypergeometrische Verteilung wird verwendet, um die Wahrscheinlichkeit zu berechnen, x Erfolge zu erzielen, wenn n Elemente aus einer Population extrahiert werden, ohne eines davon zu ersetzen.

Die hypergeometrische Verteilung hat drei Parameter:

N : ist die Anzahl der Elemente in der Population (N = 0, 1, 2,…).
K : ist die maximale Anzahl von Erfolgsfällen (K = 0, 1, 2,…,N). Da in einer hypergeometrischen Verteilung ein Element nur als „Erfolg“ oder „Misserfolg“ betrachtet werden kann, ist NK die maximale Anzahl von Misserfolgsfällen.
n : ist die Anzahl der durchgeführten Abrufe ohne Ersetzung.

$X \sim HG(N,K,n)$

Beispielsweise ist eine diskrete Zufallsvariable X, die eine hypergeometrische Verteilung mit den Parametern N=8, K=5 und n=3 aufweist, wie folgt definiert:

$X \sim HG(8,5,3)$

Hypergeometrische Verteilungsformel

Die Formel für die hypergeometrische Verteilung ist das Produkt der kombinatorischen Zahl von K über x durch die kombinatorische Zahl von NK über nx dividiert durch die kombinatorische Zahl von N über n .

Dabei ist N die Populationsgröße, K die Gesamtzahl der günstigen Fälle, n die Anzahl der ersatzlosen Extraktionen und x die Anzahl der günstigen Fälle, für die die Eintrittswahrscheinlichkeit berechnet werden muss.

👉 Mit dem Rechner unten können Sie die Wahrscheinlichkeit eines Ereignisses einer Variablen berechnen, die der hypergeometrischen Verteilung folgt.

Beispiel einer hypergeometrischen Verteilung

Nachdem wir die Definition und Formel der hypergeometrischen Verteilung gesehen haben, werden wir nun Schritt für Schritt ein Beispiel lösen, damit Sie wissen, wie Sie die Wahrscheinlichkeit einer hypergeometrischen Verteilung berechnen.

In eine Tüte legen wir 20 blaue und 30 rote Kugeln, d. h. insgesamt sind 50 Kugeln in der Tüte. Wenn wir 12 Bälle ziehen, ohne einen zu ersetzen, ermitteln Sie die Wahrscheinlichkeit, 4 blaue Bälle zu ziehen.

Um die Aufgabe zu lösen, müssen wir zunächst die Parameter der hypergeometrischen Verteilung identifizieren. In diesem Fall beträgt die Gesamtzahl der Elemente in der Grundgesamtheit 50 ( N = 50), die maximale Anzahl günstiger Fälle beträgt 20 ( K = 20) und es werden 12 Kugeln gezogen ( n = 12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

Wir möchten die Wahrscheinlichkeit berechnen, 4 blaue Kugeln zu ziehen ( x =4), also wenden wir die hypergeometrische Verteilungsformel an, ersetzen die Variablen durch ihre entsprechenden Werte und führen die Berechnung durch:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Hypergeometrischer Verteilungsrechner

Geben Sie die Parameter der hypergeometrischen Verteilung in den folgenden Online-Rechner ein, um die Eintrittswahrscheinlichkeit des gewünschten Ereignisses zu berechnen.

Denken Sie daran, dass N die Populationsgröße, K die Gesamtzahl der günstigen Fälle, n die Stichprobengröße und x der Wert ist, für den wir die Wahrscheinlichkeit dafür ermitteln möchten.

Merkmale der hypergeometrischen Verteilung

Die hypergeometrische Verteilung hat die folgenden Eigenschaften:

Der Erwartungswert einer hypergeometrischen Verteilung ist gleich der Anzahl der Elemente in der Stichprobe multipliziert mit der Gesamtzahl der günstigen Fälle dividiert durch die Anzahl der Elemente in der Grundgesamtheit.

$E[X]=\cfrac{n\cdot K}{N}$

Der Modus einer hypergeometrischen Verteilung ist der abgerundete Wert aus dem Produkt von n+1 mal K+1 dividiert durch N+2 .

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

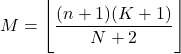
Die Varianz einer hypergeometrischen Verteilung kann mit dem folgenden Ausdruck ermittelt werden:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

Die momenterzeugende Funktion einer hypergeometrischen Verteilung ist wie folgt:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

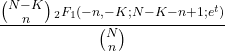
Die charakteristische Funktion der hypergeometrischen Verteilung ist wie folgt:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

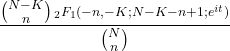
Die Eintrittswahrscheinlichkeit einer bestimmten Anzahl von Ereignissen kann aus der Wahrscheinlichkeit der vorherigen Anzahl mithilfe der Rekursive für die hypergeometrische Verteilung berechnet werden:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Hypergeometrische Verteilung und Binomialverteilung

Der Unterschied zwischen der hypergeometrischen Verteilung und der Binomialverteilung ist die Ersetzung. Hypergeometrische Verteilung wird verwendet, wenn Retrievals nicht ersetzt werden, bei der Binomialverteilung werden Retrievals jedoch ersetzt.

Wenn wir beispielsweise fünf Karten zufällig in einem Stapel ziehen und die Wahrscheinlichkeit berechnen möchten, eine bestimmte Karte zu erhalten, müssen wir für die Berechnung die hypergeometrische Verteilung verwenden, wenn wir nicht jede gezogene Karte ersetzen. Wenn wir jedoch beim Entfernen einer Karte diese vor der nächsten Extraktion wieder zurücklegen, müssen wir die Binomialverteilung verwenden, um die Wahrscheinlichkeit zu berechnen.

Wenn die Zahl N groß, das Verhältnis n/N klein und die Anzahl der gewünschten günstigen Fälle sehr klein ist, können wir die hypergeometrische Verteilung als Näherung der Binomialverteilung verwenden. Ich empfehle es jedoch nicht, da das Ergebnis nicht so zuverlässig ist und es außerdem einfacher ist, Wahrscheinlichkeiten mit dem Binomialgesetz zu berechnen als mit dem hypergeometrischen Gesetz.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen