Wahrscheinlichkeit der schnittmenge von ereignissen

In diesem Artikel wird erläutert, wie die Schnittwahrscheinlichkeit von Ereignissen berechnet wird. So erfahren Sie, wie die Formel für die Schnittwahrscheinlichkeit von Ereignissen lautet, und lösen zusätzlich Übungen Schritt für Schritt.

Was ist der Schnittpunkt der Ereignisse?

In der Wahrscheinlichkeitstheorie ist der Schnittpunkt von Ereignissen eine Operation von Ereignissen, deren Ergebnis sich aus elementaren Ereignissen zusammensetzt, die allen Ereignissen der Operation gemeinsam sind. Das heißt, der Schnittpunkt der Ereignisse A und B wird durch alle Ereignisse gebildet, die gleichzeitig zu A und B gehören.

Der Schnittpunkt zweier Ereignisse wird durch das Symbol ⋂ ausgedrückt. Somit wird der Schnittpunkt der Ereignisse A und B als A⋂B geschrieben.

Wenn zum Beispiel im Zufallsexperiment des Würfelns ein Ereignis darin besteht, dass eine gerade Zahl gewürfelt wird, A={2, 4, 6} und ein anderes Ereignis darin besteht, dass eine Zahl größer als drei gewürfelt wird, B={4, 5, 6 }, der Schnittpunkt der beiden Ereignisse ist A⋂B={4, 6}.

Formel für die Schnittwahrscheinlichkeit von Ereignissen

Die Wahrscheinlichkeit des Schnittpunkts zweier Ereignisse ist gleich der Wahrscheinlichkeit des Eintretens eines Ereignisses multipliziert mit der bedingten Wahrscheinlichkeit des Eintretens des anderen Ereignisses bei gegebenem ersten Ereignis.

Daher lautet die Formel für die Wahrscheinlichkeit des Schnittpunkts zweier Ereignisse P(A⋂B)=P(A) P(B|A)=P(B) P(A|B).

Gold:

• 

  Und

  

  Dies sind zwei abhängige Ereignisse.

• 

  ist die Wahrscheinlichkeit des Schnittpunkts von Ereignis A und Ereignis B.

• 

  ist die Wahrscheinlichkeit, dass Ereignis A eintritt.

• 

  ist die bedingte Wahrscheinlichkeit, dass Ereignis B bei gegebenem Ereignis A eintritt.

• 

  ist die Wahrscheinlichkeit, dass Ereignis B eintritt.

• 

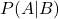
  ist die bedingte Wahrscheinlichkeit, dass Ereignis A bei gegebenem Ereignis B eintritt.

Wenn die beiden Ereignisse jedoch unabhängig sind, bedeutet dies, dass die Wahrscheinlichkeit des Eintretens eines Ereignisses nicht davon abhängt, ob das andere Ereignis eintritt. Daher lautet die Formel für die Schnittwahrscheinlichkeit der beiden unabhängigen Ereignisse wie folgt:

Gold:

• 

  Und

  

  Es handelt sich um zwei unabhängige Ereignisse.

• 

  ist die Wahrscheinlichkeit des Schnittpunkts von Ereignis A und Ereignis B.

• 

  ist die Wahrscheinlichkeit, dass Ereignis A eintritt.

• 

  ist die Wahrscheinlichkeit, dass Ereignis B eintritt.

Beispiele aus der Praxis für die Wahrscheinlichkeit von Ereignisüberschneidungen

Als nächstes lassen wir Ihnen zwei Beispiele Schritt für Schritt lösen, damit Sie sehen können, wie die Schnittwahrscheinlichkeit zweier Ereignisse berechnet wird. Wir werden zunächst ein Beispiel für den Schnittpunkt zweier unabhängiger Ereignisse und dann zweier abhängiger Ereignisse sehen, sodass Sie beide Fälle sehen können.

Wahrscheinlichkeit des Schnittpunkts zweier unabhängiger Ereignisse

• Eine Ziehung wird dreimal hintereinander gestartet. Ermitteln Sie die Wahrscheinlichkeit, bei allen drei Würfen „Kopf“ zu bekommen.

In diesem Fall sind die Ereignisse, für die wir die gemeinsame Wahrscheinlichkeit berechnen möchten, unabhängig, da das Ergebnis einer Ziehung nicht vom Ergebnis der vorherigen Ziehung abhängt. Um die Wahrscheinlichkeit zu bestimmen, drei aufeinanderfolgende Köpfe zu bekommen, müssen wir daher die Schnittwahrscheinlichkeitsformel für unabhängige Ereignisse verwenden:

Bei der Auslosung gibt es nur zwei mögliche Ergebnisse, wir können Kopf oder Zahl bekommen. Daher ist die Wahrscheinlichkeit, beim Münzwurf Kopf oder Zahl zu bekommen, wie folgt:

Um also die Wahrscheinlichkeit zu ermitteln, bei allen drei Münzwürfen Kopf zu bekommen, müssen wir die Wahrscheinlichkeit, bei allen drei Münzwürfen Kopf zu bekommen, mit drei multiplizieren:

Kurz gesagt beträgt die Wahrscheinlichkeit, dreimal hintereinander Kopf zu bekommen, 12,5 %.

Wahrscheinlichkeit des Schnittpunkts zweier abhängiger Ereignisse

• In eine leere Schachtel legen wir 8 blaue Kugeln, 4 orangefarbene Kugeln und 2 grüne Kugeln. Wenn wir zuerst einen Ball ziehen und dann einen anderen Ball, ohne den zuerst gezogenen Ball zurück in die Schachtel zu legen, wie hoch ist dann die Wahrscheinlichkeit, dass der erste Ball blau und der zweite Ball orange ist?

In diesem Fall sind die Ereignisse abhängig, da die Wahrscheinlichkeit, bei der zweiten Ziehung eine orangefarbene Kugel zu ergattern, von der Farbe der bei der ersten Ziehung gezogenen Kugel abhängt. Um die Wahrscheinlichkeit zu berechnen, die uns das Problem stellt, müssen wir daher die Formel für die Schnittwahrscheinlichkeit für abhängige Ereignisse verwenden:

Die Wahrscheinlichkeit, bei der ersten Ziehung eine blaue Kugel zu erhalten, lässt sich leicht ermitteln, indem man einfach die Anzahl der blauen Kugeln durch die Gesamtzahl der Kugeln dividiert:

Andererseits wird die Wahrscheinlichkeit, nach der Aufnahme einer blauen Kugel eine orangefarbene Kugel zu ziehen, anders berechnet, da die Anzahl der orangefarbenen Kugeln unterschiedlich ist und außerdem nun eine Kugel weniger in der Schachtel liegt:

Somit wird die Wahrscheinlichkeit, dass zuerst eine blaue Kugel und dann eine orangefarbene Kugel gezogen wird, durch Multiplikation der beiden oben gefundenen Wahrscheinlichkeiten berechnet:

Eigenschaften von Ereignis-Schnittpunkten

In der Wahrscheinlichkeitstheorie hat der Schnittpunkt von Ereignissen die folgenden Eigenschaften:

• Kommutative Eigenschaft: Die Reihenfolge der Schnittereignisse ändert das Ergebnis der Operation nicht.

• Assoziative Eigenschaft: Der Schnittpunkt dreier Ereignisse kann in beliebiger Reihenfolge berechnet werden, da das Ergebnis das gleiche ist.

• Verteilungseigenschaft: Die Schnittmenge von Ereignissen erfüllt die Verteilungseigenschaft bei der Vereinigung von Ereignissen.