Empirische wahrscheinlichkeit

In diesem Artikel erklären wir, wie man die empirische Wahrscheinlichkeit berechnet. Sie erfahren, was empirische Wahrscheinlichkeit ist, wie ihre Formel lautet, ein Beispiel und was die Unterschiede zwischen empirischer Wahrscheinlichkeit und theoretischer Wahrscheinlichkeit sind.

Was ist empirische Wahrscheinlichkeit?

Die empirische Wahrscheinlichkeit ist ein statistisches Maß, das auf empirischen Experimenten oder Fakten basiert und die Wahrscheinlichkeit des Eintretens eines Ereignisses angibt.

Mit anderen Worten: Die empirische Wahrscheinlichkeit wird aus den Ergebnissen eines Experiments berechnet und sagt uns, wie wahrscheinlich es ist, dass ein Ereignis eintritt.

Je öfter das Experiment wiederholt wird, desto genauer wird die empirische Wahrscheinlichkeit sein. Aus diesem Grund wird diese Art von Wahrscheinlichkeit normalerweise mithilfe von Computerprogrammen ermittelt, die Tausende von Iterationen simulieren und diese in sehr kurzer Zeit analysieren können.

Die empirische Wahrscheinlichkeit ist eine Zahl zwischen 0 und 1. Je wahrscheinlicher das Eintreten eines Ereignisses ist, desto höher ist die empirische Wahrscheinlichkeit, und umgekehrt: Je weniger wahrscheinlich das Eintreten eines Ereignisses ist, desto geringer ist seine empirische Wahrscheinlichkeit.

Empirische Wahrscheinlichkeitsformel

Die Formel für die empirische Wahrscheinlichkeit ist die Häufigkeit, mit der ein Ereignis während eines Experiments aufgetreten ist, geteilt durch die Gesamtzahl der Durchführungen des Experiments.

Wenn wir beispielsweise zehn Mal einen Baum betrachten und sieben Mal einen Vogel im Baum gesehen haben, beträgt die empirische Wahrscheinlichkeit, beim Betrachten des Baums einen Vogel zu sehen:

Beispiel für empirische Wahrscheinlichkeit

Unter Berücksichtigung der Definition der empirischen Wahrscheinlichkeit werden wir eine Schritt-für-Schritt-Übung zu dieser Art von Wahrscheinlichkeit lösen. Auf diese Weise können Sie sehen, wie die empirische Wahrscheinlichkeit berechnet wird.

• Berechnet die empirische Wahrscheinlichkeit der Elementarereignisse, die das Zufallsexperiment des Würfelns ausmachen.

Zunächst berechnen wir die theoretische Wahrscheinlichkeit für den Vergleich der experimentellen Ergebnisse mit den theoretischen Ergebnissen. Es gibt sechs mögliche Ergebnisse beim Würfeln (1, 2, 3, 4, 5 und 6), daher ist die theoretische Wahrscheinlichkeit jedes Elementarereignisses:

Um diese Aufgabe zu lösen, müssen wir das mehrmalige Würfeln simulieren und die Ergebnisse in einer Kontingenztabelle festhalten. Hierzu können wir beispielsweise das Excel-Programm verwenden.

Damit Sie die Bedeutung der Anzahl der durchgeführten Experimente erkennen können, werden wir zunächst zehn Starts, dann hundert und schließlich tausend Starts simulieren. Somit ergeben sich aus der Simulation der ersten 10 zufälligen Würfelwürfe folgende Ergebnisse:

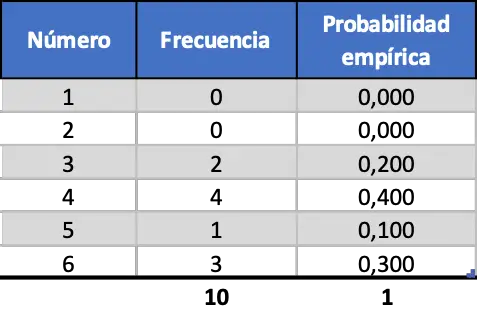
Wie Sie sehen, liegen die empirischen Wahrscheinlichkeiten, die man durch die Simulation von nur zehn Würfen erhält, nicht annähernd an den theoretischen Wahrscheinlichkeiten (0,167).

Aber wenn wir die Anzahl der Experimente erhöhen, werden diese beiden Metriken ähnlicher. Schauen Sie sich die Simulation von 100 Starts an:

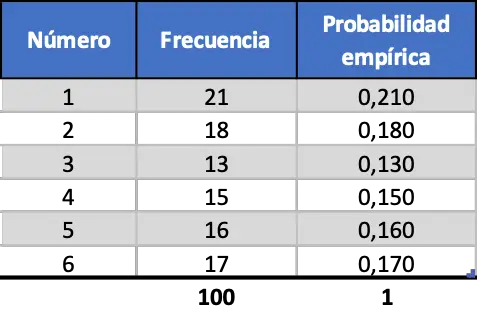
Nun ähnelt die empirische Wahrscheinlichkeit, die für jede Zahl auf dem Würfel berechnet wird, eher der theoretischen Wahrscheinlichkeit, allerdings erhalten wir immer noch sehr unterschiedliche Werte.

Schließlich führen wir das gleiche Verfahren durch, simulieren jedoch 1000 Starts:

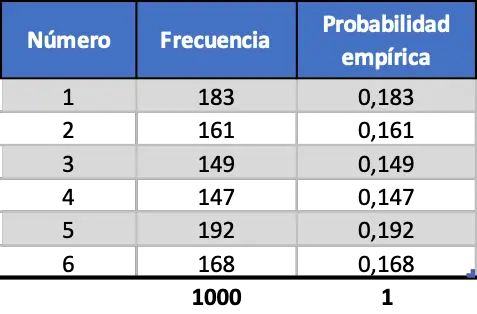
Wie wir in der letzten Kontingenztabelle sehen können, liegen die Werte der empirischen Wahrscheinlichkeiten nun sehr nahe an den theoretischen Wahrscheinlichkeiten.

Zusammenfassend gilt: Je mehr wir die Anzahl der durchgeführten Experimente erhöhen, desto näher kommt der Wert der empirischen Wahrscheinlichkeit eines Ereignisses seiner theoretischen Eintrittswahrscheinlichkeit . Diese Regel ist als Gesetz der großen Zahlen definiert, das besagt, dass die experimentellen Werte umso näher an den theoretischen Werten liegen, je mehr Daten vorhanden sind.

Wenn wir außerdem die drei Häufigkeitstabellen vergleichen, sehen wir, dass die empirische Wahrscheinlichkeit nicht definitiv ist, sondern dass sie sich je nach Anzahl der durchgeführten Experimente ändert. Das bedeutet, dass man wissen muss, wie man die erhaltenen Werte interpretiert.

Empirische Wahrscheinlichkeit und theoretische Wahrscheinlichkeit

Abschließend analysieren wir den Begriff der empirischen Wahrscheinlichkeit und den der theoretischen Wahrscheinlichkeit, denn obwohl es sich um zwei Arten von Wahrscheinlichkeiten handelt, haben sie eine völlig unterschiedliche Bedeutung.

Der Unterschied zwischen empirischer Wahrscheinlichkeit und theoretischer Wahrscheinlichkeit (oder klassischer Wahrscheinlichkeit) besteht darin, dass die empirische Wahrscheinlichkeit anhand realer Erfahrungsdaten berechnet wird, während die theoretische Wahrscheinlichkeit unter Berücksichtigung idealer Umstände berechnet wird, ohne dass ein Experiment durchgeführt wird.

Das heißt, um die empirische Wahrscheinlichkeit zu ermitteln, muss ein Experiment simuliert und die Berechnung auf der Grundlage der erhaltenen Ergebnisse durchgeführt werden. Um die theoretische Wahrscheinlichkeit zu kennen, muss jedoch kein Experiment durchgeführt werden, sondern eine theoretische Berechnung.

Darüber hinaus wird der Grad der Verzerrung als Differenz zwischen der empirischen Wahrscheinlichkeit und der theoretischen Wahrscheinlichkeit definiert. Der Bias kann positiv oder negativ sein, aber es ist sehr schwierig, dass er Null ist, denn das würde bedeuten, dass ein Zufallsexperiment gerade die theoretische Wahrscheinlichkeit erreicht, was sehr unwahrscheinlich ist.