Maße der zentralen tendenz: definition und beispiele
Ein Maß für die zentrale Tendenz ist ein einzelner Wert, der den zentralen Punkt eines Datensatzes darstellt. Dieser Wert kann auch als „zentraler Ort“ eines Datensatzes bezeichnet werden.
In der Statistik gibt es drei gängige Maßstäbe für die zentrale Tendenz:
- Der Durchschnitt
- Der Median
- Die Mode
Jede dieser Maßnahmen findet den zentralen Ort eines Datensatzes mit unterschiedlichen Methoden. Abhängig von der Art der Daten, die Sie analysieren, ist es möglicherweise besser, eine dieser drei Metriken anstelle der beiden anderen zu verwenden.
In diesem Artikel schauen wir uns an, wie Sie jedes der drei Maße der zentralen Tendenz berechnen und wie Sie anhand Ihrer Daten bestimmen, welches Maß am besten zu verwenden ist.
Warum sind Messungen der zentralen Tendenz nützlich?
Bevor wir uns mit der Berechnung von Mittelwert, Median und Modus befassen, ist es hilfreich zu verstehen , warum diese Messungen überhaupt nützlich sind.
Stellen Sie sich das folgende Szenario vor:
Ein junges Paar versucht zu entscheiden, wo es in einer neuen Stadt sein erstes Haus kaufen soll, und kann höchstens 150.000 US-Dollar ausgeben. In einigen Gegenden der Stadt gibt es teure Häuser, in anderen gibt es günstige Häuser und in anderen gibt es Häuser im mittleren Preissegment. Sie möchten ihre Suche einfach auf bestimmte Stadtteile eingrenzen, die zu ihrem Budget passen.
Wenn sich das Paar nur die Preise für Einfamilienhäuser in den einzelnen Stadtteilen ansehen würde, könnte es Schwierigkeiten haben, herauszufinden, welche Stadtteile am besten zu seinem Budget passen, weil es möglicherweise so etwas sehen würde:
Hauspreise in Nachbarschaft A : 140.000 $, 190.000 $, 265.000 $, 115.000 $, 270.000 $, 240.000 $, 250.000 $, 180.000 $, 160.000 $, 200.000 $, 240.000 $, 280.000 $, …
Hauspreise in Nachbarschaft B : 140.000 $, 290.000 $, 155.000 $, 165.000 $, 280.000 $, 220.000 $, 155.000 $, 185.000 $, 160.000 $, 200.000 $, 190.000 $, 140.000 $, 145,0 $ 0 0,…
Hauspreise in Nachbarschaft C : 140.000 $, 130.000 $, 165.000 $, 115.000 $, 170.000 $, 100.000 $, 150.000 $, 180.000 $, 190.000 $, 120.000 $, 110.000 $, 130.000 $, 120,0 $ 0 0,…
Wenn sie jedoch den Durchschnittspreis (z. B. ein Maß für die zentrale Tendenz) von Häusern in jedem Viertel kennen würden, könnten sie ihre Suche viel schneller verfeinern, da sie einfacher erkennen könnten, in welchem Viertel die Hauspreise zu ihrem Budget passen:
Durchschnittspreis eines Hauses in Nachbarschaft A: 220.000 $
Durchschnittspreis eines Hauses in Nachbarschaft B : 190.000 $
Durchschnittspreis eines Hauses in Nachbarschaft C : 140.000 $
Wenn sie den durchschnittlichen Immobilienpreis in jedem Stadtviertel kennen, können sie schnell erkennen, dass in Nachbarschaft C wahrscheinlich die meisten verfügbaren Häuser innerhalb ihres Budgets verfügbar sind.
Dies ist der Vorteil der Verwendung eines Maßes für die zentrale Tendenz: Es hilft Ihnen, den zentralen Wert eines Datensatzes zu verstehen, der tendenziell beschreibt, wo die Datenwerte im Allgemeinen liegen. In diesem speziellen Beispiel hilft es dem jungen Paar, den typischen Preis eines Hauses in jeder Nachbarschaft zu verstehen.
Fazit: Ein Maß für die zentrale Tendenz ist nützlich, weil es uns einen einzigen Wert liefert, der das „Zentrum“ eines Datensatzes beschreibt. Dies hilft uns, einen Datensatz viel schneller zu verstehen, als nur alle einzelnen Werte im Datensatz zu betrachten.
Bedeuten
Das am häufigsten verwendete Maß für die zentrale Tendenz ist der Mittelwert . Um den Durchschnitt eines Datensatzes zu berechnen, addieren Sie einfach alle Einzelwerte und dividieren durch die Gesamtzahl der Werte.
Durchschnitt = (Summe aller Werte) / (Gesamtzahl der Werte)
Angenommen, wir haben den folgenden Datensatz, der die Anzahl der Homeruns zeigt, die von 10 Baseballspielern derselben Mannschaft während einer Saison erzielt wurden:
| Spieler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #zehn |
|---|---|---|---|---|---|---|---|---|---|---|
| Home Runs | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
Die durchschnittliche Anzahl der pro Spieler erzielten Homeruns lässt sich wie folgt berechnen:
Durchschnitt = (8+15+22+21+12+9+11+27+14+13) / 10 = 15,2 Schaltkreise .
Median
Der Median ist der Mittelwert eines Datensatzes. Sie können den Median ermitteln, indem Sie alle Einzelwerte in einem Datensatz vom kleinsten zum größten ordnen und den Medianwert ermitteln. Bei einer ungeraden Anzahl an Werten ist der Median der Mittelwert. Bei einer geraden Anzahl von Werten ist der Median der Durchschnitt der beiden Mittelwerte.
Um beispielsweise die mittlere Anzahl der von den zehn Baseballspielern im vorherigen Beispiel erzielten Homeruns zu ermitteln, können wir die Spieler in absteigender Reihenfolge nach der Anzahl der erzielten Homeruns ordnen:
| Spieler | #1 | #6 | #7 | #5 | #zehn | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Home Runs | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Da wir eine gerade Anzahl von Werten haben, ist der Median einfach der Durchschnitt der beiden Mittelwerte: 13,5 .
Überlegen Sie stattdessen, ob wir neun Spieler hätten:
| Spieler | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Home Runs | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
Da wir in diesem Fall eine ungerade Anzahl von Werten haben, ist der Median einfach der Mittelwert: 14 .
Die Mode
Der Modus ist der Wert, der in einem Datensatz am häufigsten vorkommt. Ein Datensatz kann keinen Modus (wenn sich keine Werte wiederholen), einen Modus oder mehrere Modi haben.
Der folgende Datensatz hat beispielsweise keinen Modus:
| Spieler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #zehn |
|---|---|---|---|---|---|---|---|---|---|---|
| Home Runs | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Der folgende Datensatz hat einen Modus: 15 . Dies ist der Wert, der am häufigsten vorkommt.
| Spieler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #zehn |
|---|---|---|---|---|---|---|---|---|---|---|
| Home Runs | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
Der folgende Datensatz verfügt über drei Modi: 8, 15, 19 . Dies sind die Werte, die am häufigsten vorkommen.
| Spieler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #zehn |
|---|---|---|---|---|---|---|---|---|---|---|
| Home Runs | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Der Modus kann bei der Arbeit mit kategorialen Daten ein besonders nützliches Maß für die zentrale Tendenz sein, da er uns sagt, welche Kategorie am häufigsten vorkommt. Betrachten Sie beispielsweise das folgende Balkendiagramm, das die Ergebnisse einer Umfrage zur Lieblingsfarbe von Menschen zeigt:
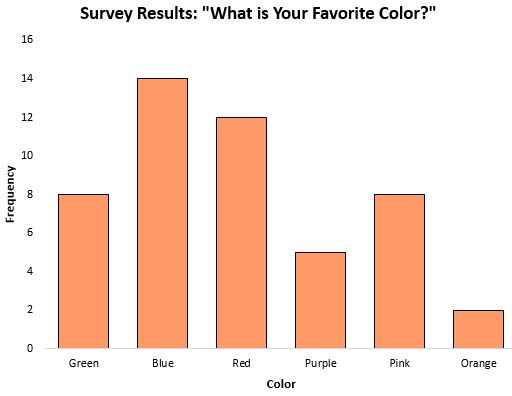
Der Modus bzw. die Antwort, die am häufigsten vorkam, war blau.
In Szenarien, in denen die Daten kategorial sind (wie oben), ist es nicht einmal möglich, den Median oder Mittelwert zu berechnen, sodass der Modus das einzige Maß für die zentrale Tendenz ist, das wir verwenden können.
Der Modus kann auch für numerische Daten verwendet werden, wie wir im obigen Beispiel mit Baseballspielern gesehen haben. Für die Beantwortung der Frage „Was ist ein typischer Wert für diesen Datensatz?“ ist der Modus jedoch tendenziell weniger nützlich. »
Angenommen, wir möchten die typische Anzahl der Homeruns eines Baseballspielers in dieser Mannschaft wissen:
| Spieler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #zehn |
|---|---|---|---|---|---|---|---|---|---|---|
| Home Runs | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Der Modus für diesen Datensatz ist 8, 15 und 19, da dies die häufigsten Werte sind. Diese sind jedoch nicht sehr hilfreich, um die typische Anzahl der von einem Spieler im Team erzielten Homeruns zu verstehen. Ein besseres Maß für die zentrale Tendenz wäre in diesem Fall der Median (15) oder der Mittelwert (ebenfalls 15).
Der Modus ist auch ein schlechtes Maß für die zentrale Tendenz, wenn es sich um eine Zahl handelt, die weit von den übrigen Werten entfernt ist. Der Modus des folgenden Datensatzes ist beispielsweise 30, aber dies stellt nicht wirklich die „typische“ Anzahl von Homeruns pro Spieler im Team dar:
| Spieler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #zehn |
|---|---|---|---|---|---|---|---|---|---|---|
| Home Runs | 5 | 6 | 7 | zehn | 11 | 12 | 13 | 15 | 30 | 30 |
Auch hier würde der Mittelwert oder Median die zentrale Position dieses Datensatzes besser beschreiben.
Wann Mittelwert, Median und Modus verwendet werden sollten
Wir haben gesehen, dass der Mittelwert, der Median und der Modus alle die zentrale Position oder den „typischen Wert“ eines Datensatzes auf sehr unterschiedliche Weise messen:
Durchschnitt: Ermittelt den Durchschnittswert in einem Datensatz.
Median: Ermittelt den Medianwert in einem Datensatz.
Modus: Findet den häufigsten Wert in einem Datensatz.
Hier sind Szenarien, in denen bestimmte Maße der zentralen Tendenz besser zu verwenden sind als andere:
Wann sollte der Durchschnitt verwendet werden?
Am besten verwenden Sie den Durchschnitt, wenn die Datenverteilung ziemlich symmetrisch ist und keine Ausreißer vorhanden sind.
Angenommen, wir haben die folgende Verteilung, die die Gehälter von Einzelpersonen in einer bestimmten Stadt zeigt:

Da diese Verteilung ziemlich symmetrisch ist (d. h. wenn man sie in zwei Hälften aufteilt, würde jede Hälfte ungefähr gleich aussehen) und es keine Ausreißer gibt (z. B. keine extrem hohen Gehälter), kann der Durchschnitt diesen Datensatz gut beschreiben.
Der Durchschnitt liegt bei 63.000 US-Dollar, was ungefähr in der Mitte der Verteilung liegt:

Wann ist der Median zu verwenden?
Es ist am besten, den Median zu verwenden, wenn die Datenverteilung verzerrt ist oder Ausreißer vorhanden sind.
Verzerrte Daten:
Wenn die Verteilung schief ist, gelingt es dem Median immer noch, die zentrale Position zu erfassen. Betrachten Sie beispielsweise die folgende Verteilung der Gehälter von Einzelpersonen in einer bestimmten Stadt:

Der Median spiegelt das „typische“ Gehalt einer Person besser wider als der Durchschnitt. Dies liegt daran, dass große Werte am Ende einer Verteilung dazu neigen, den Mittelwert von der Mitte weg und in Richtung des langen Endes zu verschieben.
In diesem speziellen Beispiel sagt uns der Durchschnitt, dass eine typische Person in dieser Stadt etwa 47.000 US-Dollar pro Jahr verdient, während der Median uns sagt, dass die typische Person nur etwa 32.000 US-Dollar pro Jahr verdient, was für die typische Person viel repräsentativer ist.
Ausreißer:
Der Median hilft auch dabei, die zentrale Position einer Verteilung besser zu erfassen, wenn die Daten Ausreißer enthalten. Betrachten Sie beispielsweise die folgende Grafik, die die Quadratmeterzahl von Häusern in einer bestimmten Straße zeigt:

Der Durchschnitt wird stark von einigen wenigen extrem großen Häusern beeinflusst, während dies beim Median nicht der Fall ist. Somit erfasst der Median die „typische“ Quadratmeterzahl eines Hauses in dieser Straße besser als der Durchschnitt.
Wann sollte der Modus verwendet werden?
Dieser Modus eignet sich am besten, wenn Sie mit kategorialen Daten arbeiten und wissen möchten, welche Kategorie am häufigsten vorkommt. Hier sind einige Beispiele:
- Sie führen eine Umfrage zu den Lieblingsfarben der Menschen durch und möchten wissen, welche Farbe in den Antworten am häufigsten vorkommt.
- Sie führen eine Umfrage zu den Präferenzen der Menschen unter drei Optionen für das Website-Design durch und möchten wissen, welches Design die Leute am meisten bevorzugen.
Wie bereits erwähnt, ist es bei der Arbeit mit kategorialen Daten nicht einmal möglich, den Median oder Mittelwert zu berechnen, sodass der Modus das einzige Maß für die zentrale Tendenz bleibt.
Wenn Sie mit numerischen Daten wie der Quadratmeterzahl von Häusern, der Anzahl der erzielten Homeruns pro Spieler, dem Gehalt pro Person usw. arbeiten, ist es im Allgemeinen am besten, den Median oder Durchschnitt zu verwenden, um den „typischen“ Wert zu beschreiben Der Datensatz.
Hinweis: Es ist wichtig zu beachten, dass bei einer vollkommen normalverteilten Datenmenge Mittelwert, Median und Modus alle denselben Wert haben.