Experimentelle wahrscheinlichkeit
Hier erfahren Sie, was die experimentelle Wahrscheinlichkeit bedeutet und wie die experimentelle Wahrscheinlichkeit berechnet wird. Darüber hinaus können Sie ein Schritt-für-Schritt-Lösungsbeispiel zur Berechnung der experimentellen Wahrscheinlichkeit sehen.
Was ist experimentelle Wahrscheinlichkeit?
Die experimentelle Wahrscheinlichkeit ist ein statistisches Maß, das auf den Ergebnissen eines Experiments oder empirischen Fakten basiert und die Wahrscheinlichkeit des Eintretens eines Ereignisses angibt.
Darüber hinaus ist die erhaltene experimentelle Wahrscheinlichkeit umso präziser, je öfter das Experiment wiederholt wird. Aus diesem Grund werden im Allgemeinen Computerprogramme verwendet, die in der Lage sind, Tausende von Experimenten schnell zu simulieren, um die experimentelle Wahrscheinlichkeit zu bestimmen und so eine bessere Präzision zu erzielen.
Die experimentelle Wahrscheinlichkeit wird auch als empirische Wahrscheinlichkeit oder Häufigkeitswahrscheinlichkeit bezeichnet.
Die experimentelle Wahrscheinlichkeit ist eine Zahl zwischen 0 und 1. Logischerweise ist es umso wahrscheinlicher, dass ein Ereignis eintritt, je größer der Wert der experimentellen Wahrscheinlichkeit ist, und umgekehrt: Je kleiner der Wert, desto unwahrscheinlicher ist es, dass es eintritt. wird wahrscheinlich auftreten. oder das Ereignis eintritt. Der Wert der experimentellen Wahrscheinlichkeit wird jedoch immer zwischen Null und Eins liegen.
Experimentelle Wahrscheinlichkeitsformel
Die Formel für die experimentelle Wahrscheinlichkeit ist die Häufigkeit, mit der ein Ereignis während eines Experiments aufgetreten ist, geteilt durch die Gesamtzahl der Durchführungen des Experiments.
![]()
Wenn eine Person beispielsweise zehn Pfeile auf eine Zielscheibe wirft und es schafft, sechs Pfeile in der Mitte zu treffen, wird die Wahrscheinlichkeit, dass diese Person einen Pfeil in der Mitte trifft, wie folgt berechnet:
![]()
Beispiel für experimentelle Wahrscheinlichkeit
Sobald wir die mathematische Definition der experimentellen Wahrscheinlichkeit kennen, werden wir eine Schritt-für-Schritt-Übung zu dieser Art von Wahrscheinlichkeit lösen. Das Ziel besteht darin, dass Sie lernen, wie die experimentelle Wahrscheinlichkeit eines Ereignisses berechnet wird. Wenn Sie also Fragen haben, können Sie diese in die Kommentare schreiben.
- Berechnen Sie die experimentelle Wahrscheinlichkeit der Elementarereignisse, die das Zufallsexperiment des Würfelns ausmachen.
Bevor wir die experimentelle Wahrscheinlichkeit ermitteln, berechnen wir die theoretische Wahrscheinlichkeit, um die erhaltenen experimentellen Ergebnisse mit den theoretischen Ergebnissen zu vergleichen. Wie Sie wissen, gibt es beim Würfeln sechs mögliche Ergebnisse (1, 2, 3, 4, 5 und 6). Die theoretische Wahrscheinlichkeit jedes Elementarereignisses beträgt also:
![]()
Um diese Aufgabe zu lösen, müssen wir das mehrmalige Würfeln simulieren und die Ergebnisse in einer Kontingenztabelle festhalten. In diesem Fall führen wir die Simulationen mit dem Excel-Programm durch, Sie können aber natürlich auch das Programm Ihrer Wahl verwenden.
Wir werden zunächst zehn Würfe simulieren, dann hundert Würfe und schließlich tausend Würfe. Auf diese Weise können wir die Ergebnisse analysieren und sehen, wie sie sich je nach Stichprobengröße des Experiments ändern. Die nach der Zufallssimulation von 10 Würfelwürfen erhaltenen Ergebnisse lauten wie folgt:
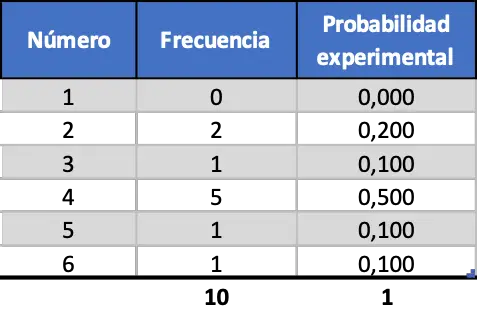
Wie Sie sehen, unterscheiden sich die experimentell ermittelten Wahrscheinlichkeiten derzeit erheblich von den zuvor berechneten theoretischen Wahrscheinlichkeiten (0,167).
Aber wenn wir die Anzahl der Tests erhöhen, werden diese beiden Metriken ähnlicher. Schauen Sie sich die Simulation von 100 Starts an:
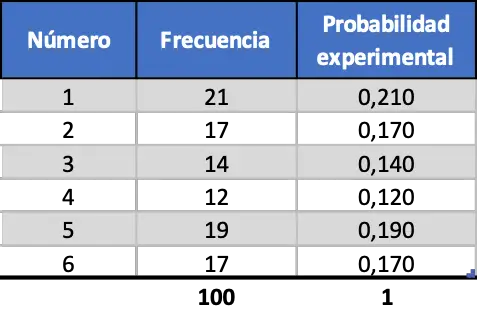
Jetzt ähnelt die experimentelle Wahrscheinlichkeit eher dem theoretischen Wahrscheinlichkeitswert, wir erhalten jedoch immer noch weit entfernte Werte.
Schließlich führen wir das gleiche Verfahren durch, simulieren jedoch 1000 Starts:
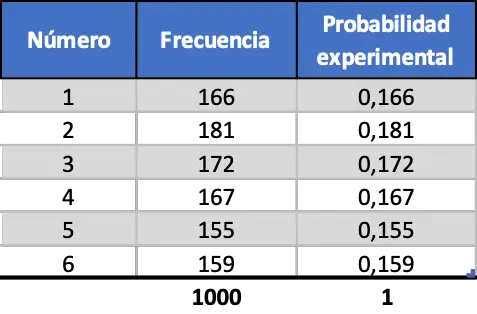
Wie Sie in der letzten Kontingenztabelle sehen können, sind die Werte der experimentellen Wahrscheinlichkeiten nun den theoretischen Wahrscheinlichkeiten sehr ähnlich.
Zusammenfassend lässt sich sagen, dass der Wert der experimentellen Wahrscheinlichkeit eines Ereignisses umso näher an seiner theoretischen Wahrscheinlichkeit liegt, je größer die Anzahl der durchgeführten Experimente ist . Diese Regel ist als Gesetz der großen Zahlen definiert, das besagt, dass die experimentellen Werte umso näher an den theoretischen Werten liegen, je mehr Daten vorhanden sind.
Wenn Sie die drei Häufigkeitstabellen vergleichen, werden Sie ebenfalls feststellen, dass die experimentelle Wahrscheinlichkeit nicht endgültig ist, sondern dass sie sich abhängig von der Anzahl der durchgeführten Experimente entwickelt. Das bedeutet, dass man wissen muss, wie man die erhaltenen Werte interpretiert.
Experimentelle Wahrscheinlichkeit und theoretische Wahrscheinlichkeit
Der Unterschied zwischen experimenteller Wahrscheinlichkeit und theoretischer Wahrscheinlichkeit (oder klassischer Wahrscheinlichkeit) besteht darin, dass die experimentelle Wahrscheinlichkeit anhand von Daten berechnet wird, die bei einem realen Experiment gesammelt wurden, während die theoretische Wahrscheinlichkeit berechnet wird, ohne dass die Durchführung eines Experiments erforderlich ist.
Wie wir gesehen haben, müssen wir eine große Anzahl von Experimenten simulieren, um die experimentelle Wahrscheinlichkeit eines Ereignisses abzuleiten. Die Berechnung der theoretischen Wahrscheinlichkeit hängt jedoch von Theorie und Logik ab. Wie es geht, können Sie hier sehen: