So führen sie eine schrittweise regression in sas durch (mit beispiel)
Schrittweise Regression ist ein Verfahren, mit dem wir ein Regressionsmodell aus einer Reihe von Prädiktorvariablen erstellen können, indem wir Prädiktoren Schritt für Schritt in das Modell eingeben und entfernen, bis es keinen statistisch gültigen Grund mehr für die Eingabe von oder gibt mehr löschen.
Das Ziel der schrittweisen Regression besteht darin, ein Regressionsmodell zu erstellen, das alle Prädiktorvariablen umfasst, die statistisch signifikant mit der Antwortvariablen zusammenhängen.
Um eine schrittweise Regression in SAS durchzuführen, können Sie PROC REG mit der SELECTION- Anweisung verwenden.
Das folgende Beispiel zeigt, wie man in der Praxis eine schrittweise Regression in SAS durchführt.
Beispiel: Durchführen einer schrittweisen Regression in SAS
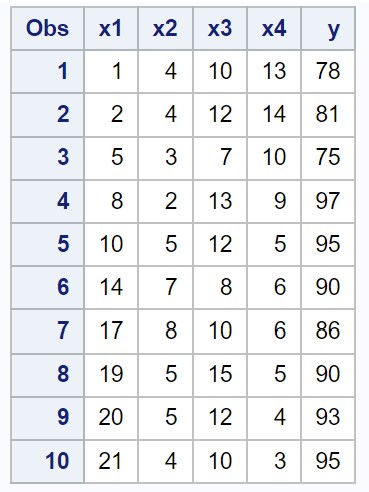
Angenommen, wir haben den folgenden Datensatz in SAS, der vier Prädiktorvariablen (x1, x2, x3, x4) und eine Antwortvariable (y) enthält:
/*create dataset*/ data my_data; input x1 x2 x3 x4 y; datalines ; 1 4 10 13 78 2 4 12 14 81 5 3 7 10 75 8 2 13 9 97 10 5 12 5 95 14 7 8 6 90 17 8 10 6 86 19 5 15 5 90 20 5 12 4 93 21 4 10 3 95 ; run ; /*view dataset*/ proc print data =my_data;
Nehmen wir nun an, wir möchten bestimmen, welche Kombination von Prädiktorvariablen das beste multiple lineare Regressionsmodell ergibt.
Wenn wir vom „besten“ Regressionsmodell sprechen, meinen wir das Modell, das bestimmte Maße maximiert oder minimiert.
Es gibt zwei Metriken, die wir üblicherweise verwenden, um zu bewerten, welches Regressionsmodell aus einer Gruppe potenzieller Modelle das beste ist:
1. Angepasstes R-Quadrat : Der angepasste R-Quadrat-Wert sagt uns die Nützlichkeit eines Modells, angepasst basierend auf der Anzahl der Prädiktoren in einem Modell. Das Modell mit dem höchsten angepassten R-Quadrat-Wert gilt als das beste.
2. AIC : Das Akaike Information Criterion (AIC) ist eine Metrik, die zum Vergleich der Passung verschiedener Regressionsmodelle verwendet wird. Das Modell mit dem niedrigsten AIC-Wert gilt als das beste.
Glücklicherweise können wir mithilfe von PROC REG mit der SELECTION- Anweisung sowohl die angepassten R-Quadrat- als auch die AIC-Werte für Regressionsmodelle in SAS berechnen.
Der folgende Code zeigt, wie das geht:
/*perform stepwise multiple linear regression*/ proc reg data =my_data outest =est; model y=x1 x2 x3 x4 / selection=adjrsq aic ; output out =out p=pr=r; run ; quit ;
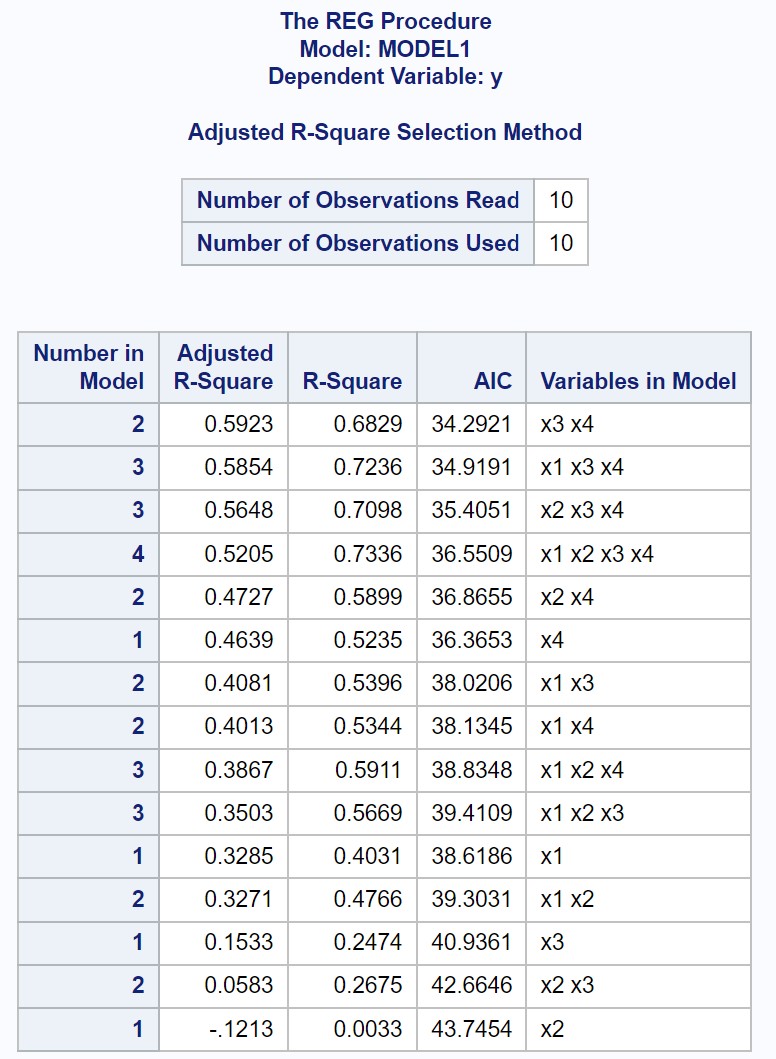
Die Ausgabe zeigt die angepassten R-Quadrat- und AIC-Werte für jedes mögliche multiple lineare Regressionsmodell an.
Aus dem Ergebnis können wir ersehen, dass der Wert mit dem höchsten angepassten R-Quadrat-Wert und dem niedrigsten AIC-Wert das Regressionsmodell ist, das nur x3 und x4 als Prädiktorvariablen verwendet.
Daher erklären wir, dass das folgende Modell „das Beste“ unter allen möglichen Modellen ist:
y = b 0 + b 1 (x3) + b 2 (x4)
Dieses spezielle Regressionsmodell weist die folgenden Metriken auf:
- Angepasster R-Quadrat-Wert: 0,5923
- AIC: 34.2921
Hinweise zur Auswahl des „besten“ Regressionsmodells
Beachten Sie, dass das Modell mit dem höchsten angepassten R-Quadrat-Wert manchmal nicht immer auch den niedrigsten AIC-Wert aufweist.
Wenn es um die Entscheidung geht, welches Regressionsmodell das beste ist, dienen das angepasste R-Quadrat und der AIC als Vorschläge, aber in der realen Welt müssen Sie möglicherweise Domänenexpertise nutzen, um zu bestimmen, welches Modell das beste ist.
Es kann auch sinnvoll sein, ein sparsames Modell zu wählen, also ein Modell, das mit möglichst wenigen Prädiktorvariablen den gewünschten Grad an Anpassung erreicht.
Der Grundgedanke hinter diesem Modelltyp geht auf die Idee von Occams Rasiermesser (manchmal auch „Sparsamkeitsprinzip“ genannt) zurück, die besagt, dass die einfachste Erklärung wahrscheinlich die richtige ist.
Auf die Statistik angewendet sollte ein Modell, das über wenige Parameter verfügt, aber ein zufriedenstellendes Maß an Anpassung erreicht, einem Modell vorgezogen werden, das über viele Parameter verfügt und nur ein geringfügig höheres Maß an Anpassung erreicht.
Zusätzliche Ressourcen
In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:
So führen Sie eine einfache lineare Regression in SAS durch
So führen Sie eine multiple lineare Regression in SAS durch
So führen Sie eine Polynomregression in SAS durch
So führen Sie eine logistische Regression in SAS durch