So berechnen sie den aic in sas (mit beispiel)

Das Akaike Information Criterion (AIC) ist eine Metrik, die zum Vergleich der Passung mehrerer Regressionsmodelle verwendet wird.

Es wird wie folgt berechnet:

AIC = 2K – 2 ln (L)

Gold:

• K: Die Anzahl der Modellparameter. Der Standardwert von K ist 2, sodass ein Modell mit nur einer Prädiktorvariablen einen K-Wert von 2+1 = 3 hat.
• ln (L) : Die Log-Likelihood des Modells. Die meisten Statistikprogramme können diesen Wert automatisch für Sie berechnen.

AIC soll das Modell finden, das die größte Variation in den Daten erklärt, und gleichzeitig Modelle bestrafen, die eine übermäßige Anzahl von Parametern verwenden.

Nachdem Sie mehrere Regressionsmodelle angepasst haben, können Sie den AIC-Wert jedes Modells vergleichen. Je niedriger der AIC, desto geeigneter ist das Modell.

Das folgende Beispiel zeigt, wie der AIC für verschiedene Regressionsmodelle in SAS berechnet wird.

Beispiel: So berechnen Sie AIC in SAS

Angenommen, wir möchten drei verschiedene multiple lineare Regressionsmodelle anpassen, um die Prüfungsnote vorherzusagen, die Schüler in einer Klasse erreichen werden.

Hier sind die Prädiktorvariablen, die wir in jedem Modell verwenden werden:

• Prädiktorvariablen in Modell 1: Lernstunden
• Prädiktorvariablen in Modell 2: vergangene praktische Prüfungen
• Prädiktorvariablen in Modell 3: Lernstunden und abgelegte Übungsprüfungen

Zuerst verwenden wir den folgenden Code, um einen Datensatz mit diesen Informationen für 20 Schüler zu erstellen:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Als Nächstes verwenden wir proc reg , um jedes dieser Regressionsmodelle anzupassen, und verwenden die aic-Anweisung „selection=adjrsq sse“, um die AIC-Werte für jedes Modell zu berechnen:

 /*fit multiple linear regression models and calculate AIC for each model*/
proc reg data =exam_data;
    model score = hours prep_exams / selection=adjrsq sse aic;
run ; 

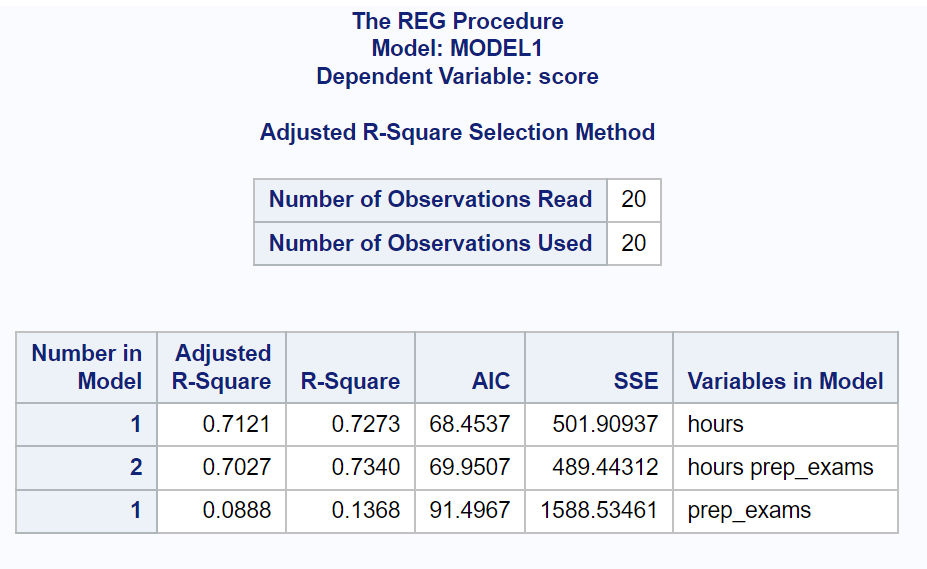
Aus dem Ergebnis können wir die AIC-Werte für jedes Modell sehen:

• AIC mit Stunden als Prädiktorvariable: 68,4537
• AIC mit Stunden und Prüfungen als Prädiktorvariablen: 69,9507
• AIC mit Prüfungen als Vorhersagevariable: 91,4967

Das Modell mit dem niedrigsten AIC-Wert ist dasjenige, das nur Stunden als Prädiktorvariable enthält.

Daher erklären wir, dass das folgende Modell am besten zu den Daten passt:

Punktzahl = β ₀ + β ₁ (Studienstunden)

Sobald wir dieses Modell als das beste Modell identifiziert haben, können wir es anpassen und die Ergebnisse analysieren, einschließlich des R-Quadrat-Werts und der Beta-Koeffizienten, um die genaue Beziehung zwischen den Lernstunden und der Schülernote zu bestimmen. ‚Abschlussprüfung.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:

So führen Sie eine einfache lineare Regression in SAS durch
So führen Sie eine multiple lineare Regression in SAS durch
So berechnen Sie das R-Quadrat in SAS
So berechnen Sie RMSE in SAS