So erstellen sie eine korrelationsmatrix in sas (mit beispiel)

Eine Korrelationsmatrix ist eine quadratische Tabelle, die die Korrelationskoeffizienten zwischen Variablen in einem Datensatz anzeigt.

Es bietet eine schnelle Möglichkeit, die Stärke linearer Beziehungen zu verstehen, die zwischen Variablen in einem Datensatz bestehen.

Sie können die PROC CORR- Anweisung in SAS verwenden, um eine Korrelationsmatrix für einen bestimmten Datensatz zu erstellen:

 /*create correlation matrix using all numeric variables in my_data*/
proc corr data =my_data;
run ;

Standardmäßig wird dadurch eine Matrix erstellt, die die Korrelationskoeffizienten zwischen allen numerischen Variablen im Datensatz anzeigt.

Um nur bestimmte Variablen in die Korrelationsmatrix aufzunehmen, können Sie die VAR- Anweisung verwenden:

 /*create correlation matrix using only var1, var2 and var3 in my_data*/
proc corr data =my_data;
    var var1, var2, var3;
run ;

Das folgende Beispiel zeigt, wie eine Korrelationsmatrix in SAS erstellt wird.

Beispiel: Erstellen einer Korrelationsmatrix in SAS

Angenommen, wir haben in SAS den folgenden Datensatz, der Informationen über verschiedene Basketballspieler enthält:

 /*create dataset*/
data my_data;
    input team $ assists rebounds points;
    datalines ;
A 4 12 22
A 5 14 24
A 5 13 26
A 6 7 26
B 7 8 29
B 8 8 32
B 8 9 20
B 10 13 14
;
run ;

/*view dataset*/
proc print data =my_data; 

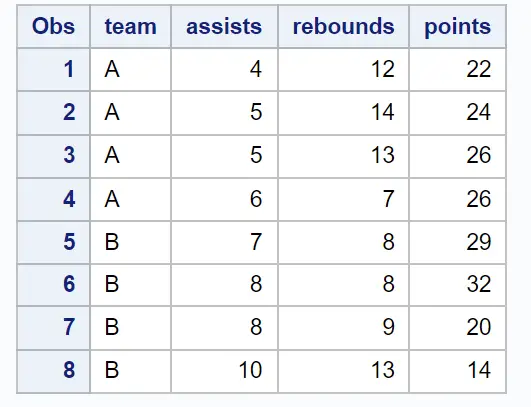
Mit der PROC CORR- Anweisung können wir eine Korrelationsmatrix erstellen, die standardmäßig jede numerische Variable im Datensatz enthält:

 /*create correlation matrix using all numeric variables in my_data*/
proc corr data =my_data;
run ; 

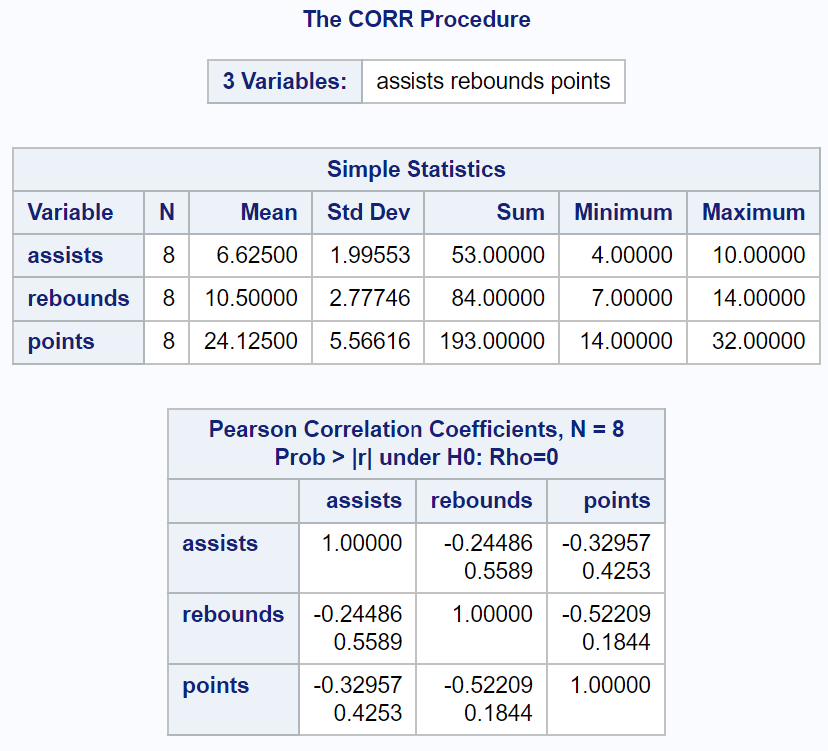
Die Ausgabe zeigt zusammenfassende Statistiken der numerischen Variablen in der ersten Tabelle zusammen mit einer Korrelationsmatrix an.

Beachten Sie, dass die Variable „Team“ nicht in der Korrelationsmatrix enthalten war, da es sich nicht um eine numerische Variable handelte.

So interpretieren Sie die Korrelationsmatrixwerte:

(1) Der Pearson-Korrelationskoeffizient (r) zwischen Assists und Rebounds beträgt -0,24486 . Der entsprechende p-Wert beträgt 0,5589 .

Da r kleiner als Null ist, bedeutet dies, dass zwischen diesen beiden Variablen ein negativer linearer Zusammenhang besteht. Da der p-Wert jedoch nicht kleiner als 0,05 ist, ist dieser Zusammenhang statistisch nicht signifikant.

(2) Der Pearson-Korrelationskoeffizient (r) zwischen Assists und Punkten beträgt -0,32957 . Der entsprechende p-Wert beträgt 0,4253 .

Es besteht ein negativer linearer Zusammenhang zwischen diesen beiden Variablen, der jedoch statistisch nicht signifikant ist.

(3) Der Pearson-Korrelationskoeffizient (r) zwischen Rebounds und Punkten beträgt -0,52209 . Der entsprechende p-Wert beträgt 0,1844 .

Es besteht ein negativer linearer Zusammenhang zwischen diesen beiden Variablen, der jedoch statistisch nicht signifikant ist.

Beachten Sie, dass wir die VAR- Anweisung auch verwenden könnten, um nur bestimmte numerische Variablen in die Korrelationsmatrix aufzunehmen:

 /*create correlation matrix using only assists and rebounds variables*/
proc corr data =my_data;
    var assists rebounds;
run ; 

Beachten Sie, dass in dieser Korrelationsmatrix nur die Assists- und Rebounds -Variablen berücksichtigt wurden.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:

So erstellen Sie eine Streudiagrammmatrix in SAS
So erstellen Sie PivotTables in SAS
So berechnen Sie den Variance Inflation Factor (VIF) in SAS