So führen sie den tukey-test in sas durch

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.

Wenn der Gesamt -p-Wert der ANOVA-Tabelle unter einem bestimmten Signifikanzniveau liegt, verfügen wir über ausreichende Beweise dafür, dass sich mindestens einer der Gruppenmittelwerte von den anderen unterscheidet.

Dies sagt uns jedoch nicht, welche Gruppen sich voneinander unterscheiden. Dies zeigt uns einfach, dass nicht alle Gruppendurchschnitte gleich sind.

Um genau zu wissen, welche Gruppen sich voneinander unterscheiden, müssen wir einenPost-hoc-Test durchführen.

Einer der am häufigsten verwendeten Post-hoc-Tests ist der Tukey-Test , der es uns ermöglicht, paarweise Vergleiche zwischen den Mittelwerten jeder Gruppe durchzuführen und gleichzeitig die Familienfehlerrate zu kontrollieren.

Das folgende Beispiel zeigt, wie der Tukey-Test in R durchgeführt wird.

Beispiel: Tukey-Test in SAS

Angenommen, ein Forscher rekrutiert 30 Studenten für die Teilnahme an einer Studie. Den Studierenden wird nach dem Zufallsprinzip eine von drei Lernmethoden zugewiesen , um sich auf eine Prüfung vorzubereiten.

Die Prüfungsergebnisse für jeden Studenten sind unten aufgeführt:

Wir können den folgenden Code verwenden, um diesen Datensatz in SAS zu erstellen:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Als nächstes verwenden wir proc ANOVA , um die einfaktorielle ANOVA durchzuführen:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
classMethod ;
modelScore = Method;
means Method / tukey cldiff ;
run ;

Hinweis : Wir haben die Mittelanweisung zusammen mit den Optionen tukey und cldiff verwendet, um anzugeben, dass ein Tukey-Post-hoc-Test (mit Konfidenzintervallen) durchgeführt werden soll, wenn der Gesamt-p-Wert der einfaktoriellen ANOVA statistisch signifikant ist. bedeutsam.

Zuerst analysieren wir die ANOVA-Tabelle im Ergebnis:

Aus dieser Tabelle können wir sehen:

• Gesamt-F-Wert: 5,26
• Der entsprechende p-Wert: 0,0140

Denken Sie daran, dass eine einfaktorielle ANOVA die folgenden Null- und Alternativhypothesen verwendet:

• H ₀ : Alle Gruppenmittelwerte sind gleich.
• H _A : Mindestens ein Gruppendurchschnitt ist unterschiedlich   ausruhen.

Da der p-Wert der ANOVA-Tabelle (0,0140) kleiner als α = 0,05 ist, lehnen wir die Nullhypothese ab.

Dies zeigt uns, dass die durchschnittliche Prüfungspunktzahl bei allen drei Lernmethoden nicht gleich ist.

Verwandte Themen: So interpretieren Sie den F-Wert und den P-Wert in der ANOVA

Um genau zu bestimmen, welche Gruppenmittelwerte unterschiedlich sind, müssen wir uns auf die endgültige Ergebnistabelle beziehen, die die Ergebnisse der Post-hoc-Tests von Tukey zeigt:

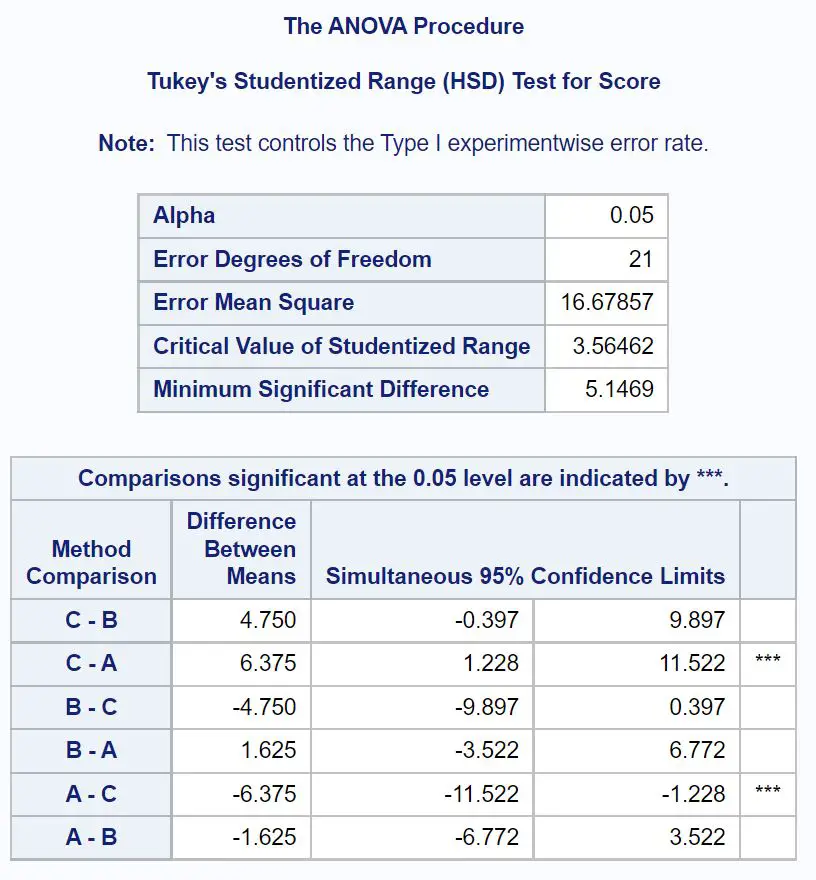
Um herauszufinden, welche Gruppenmittelwerte unterschiedlich sind, müssen wir uns ansehen, bei welchen paarweisen Vergleichen Sterne ( *** ) neben ihnen stehen.

Aus der Tabelle können wir ersehen, dass es einen statistisch signifikanten Unterschied in den durchschnittlichen Prüfungsergebnissen zwischen Gruppe A und Gruppe C gibt.

Es gibt keine statistisch signifikanten Unterschiede zwischen den Mittelwerten der anderen Gruppen.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu ANOVA-Modellen:

Ein Leitfaden zur Verwendung von Post-Hoc-Tests mit ANOVA
So führen Sie eine einfaktorielle ANOVA in SAS durch
So führen Sie eine zweifaktorielle ANOVA in SAS durch