So berechnen sie schiefe und kurtosis in sas
In der Statistik sind Schiefe und Kurtosis zwei Möglichkeiten, die Form einer Verteilung zu messen.
Schiefe misst die Asymmetrie einer Verteilung.
- Eine negative Schiefe zeigt an, dass sich das Ende auf der linken Seite der Verteilung befindet.
- Eine positive Schiefe zeigt an, dass sich das Ende auf der rechten Seite der Verteilung befindet.
- Ein Wert von Null zeigt an, dass die Verteilung keine Asymmetrie aufweist, was bedeutet, dass die Verteilung vollkommen symmetrisch ist.
Kurtosis misst, ob eine Verteilung im Vergleich zu einerNormalverteilung stark oder schwach ausgeprägt ist.
- Die Kurtosis einer Normalverteilung beträgt 0.
- Wenn eine bestimmte Verteilung eine Kurtosis kleiner als 0 aufweist, spricht man von einer Playkurtic- Verteilung, was bedeutet, dass sie tendenziell weniger und weniger extreme Ausreißer als die Normalverteilung erzeugt.
- Wenn eine bestimmte Verteilung eine Kurtosis größer als 0 aufweist, spricht man von einer leptokurtischen Verteilung, was bedeutet, dass sie tendenziell mehr Ausreißer als die Normalverteilung erzeugt.
Um die Schiefe und Kurtosis von Variablen in SAS zu berechnen, können Sie die Anweisungen SKEWNESS und KURTOSIS in PROC MEANS verwenden.
Das folgende Beispiel zeigt, wie Sie diese Anleitung in der Praxis anwenden können.
Beispiel: Berechnung von Schiefe und Kurtosis in SAS
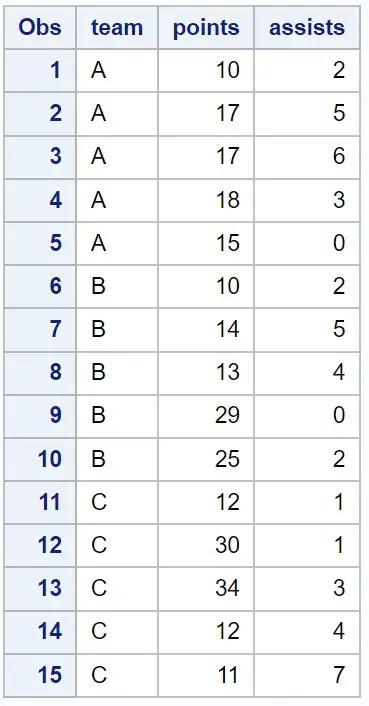
Angenommen, wir haben in SAS den folgenden Datensatz, der Informationen über verschiedene Basketballspieler enthält:
/*create dataset*/ data my_data; input team $points assists; datalines ; At 10 2 At 17 5 At 17 6 At 18 3 At 15 0 B 10 2 B 14 5 B 13 4 B 29 0 B 25 2 C 12 1 C 30 1 C 34 3 C 12 4 C 11 7 ; run ; /*view dataset*/ proc print data =my_data;
Wir können PROC MEANS mit den Anweisungen SKEWNESS und KURTOSIS verwenden, um die Schiefe und Kurtosis jeder numerischen Variablen im Datensatz zu berechnen:
/*calculate skewness and kurtosis for each numeric variable*/ proc means data =my_data SKEWNESS KURTOSIS ; run ;
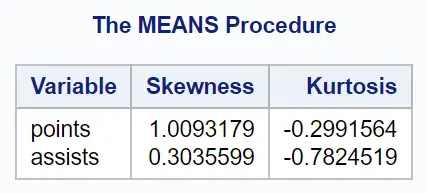
Die Ausgabetabelle zeigt die Schiefe- und Kurtosis-Werte für jede numerische Variable im Datensatz an:
(1) Punkte
- Die Punktevariable hat eine Schiefe von 1,009 . Da dieser Wert größer als 0 ist, bedeutet dies, dass sich das Ende auf der rechten Seite der Verteilung befindet.
- Die Punktevariable hat eine Kurtosis von -0,299 . Da dieser Wert kleiner als 0 ist, bedeutet dies, dass die Verteilung etwas weniger Ausreißer und weniger Extremwerte aufweist als die Normalverteilung.
(2) Hilfe
- Die Assists-Variable hat eine Schiefe von 0,304 . Da dieser Wert größer als 0 ist, bedeutet dies, dass sich das Ende auf der rechten Seite der Verteilung befindet.
- Die Unterstützungsvariable hat eine Kurtosis von -0,782 . Da dieser Wert kleiner als 0 ist, bedeutet dies, dass die Verteilung weniger Ausreißer und weniger Extremwerte aufweist als die Normalverteilung.
Um die Werteverteilung für jede numerische Variable im Datensatz zu visualisieren, können Sie mit PROC UNIVARIATE Histogramme für die Punkt- und Hilfsvariablen erstellen:
/*create histograms for points and assists variables*/
proc univariate data =my_data;
var points assists;
histogram points assists;
run ;
Dadurch entsteht das folgende Histogramm für die Punktevariable :
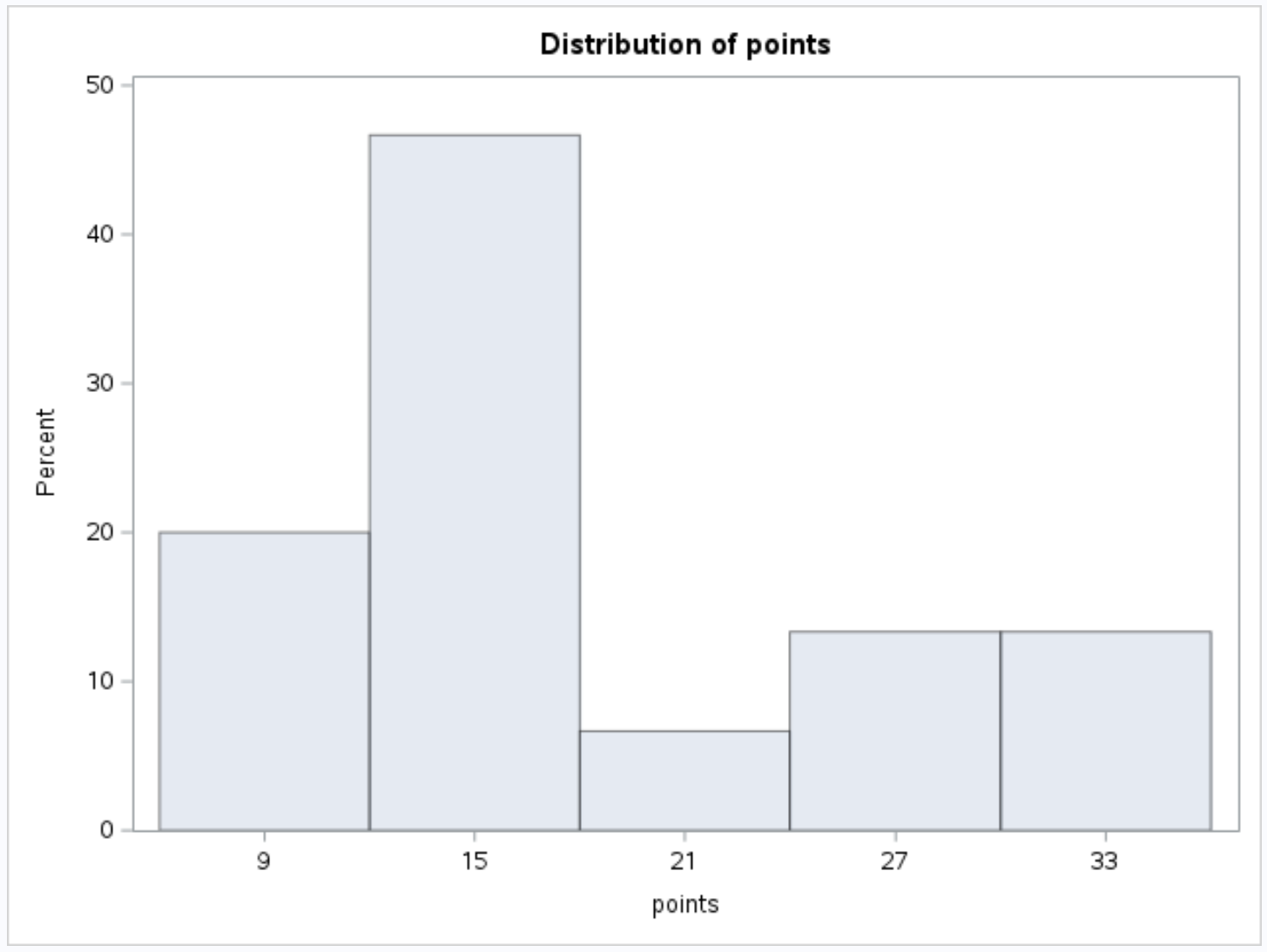
Und das folgende Histogramm für die Hilfsvariable :
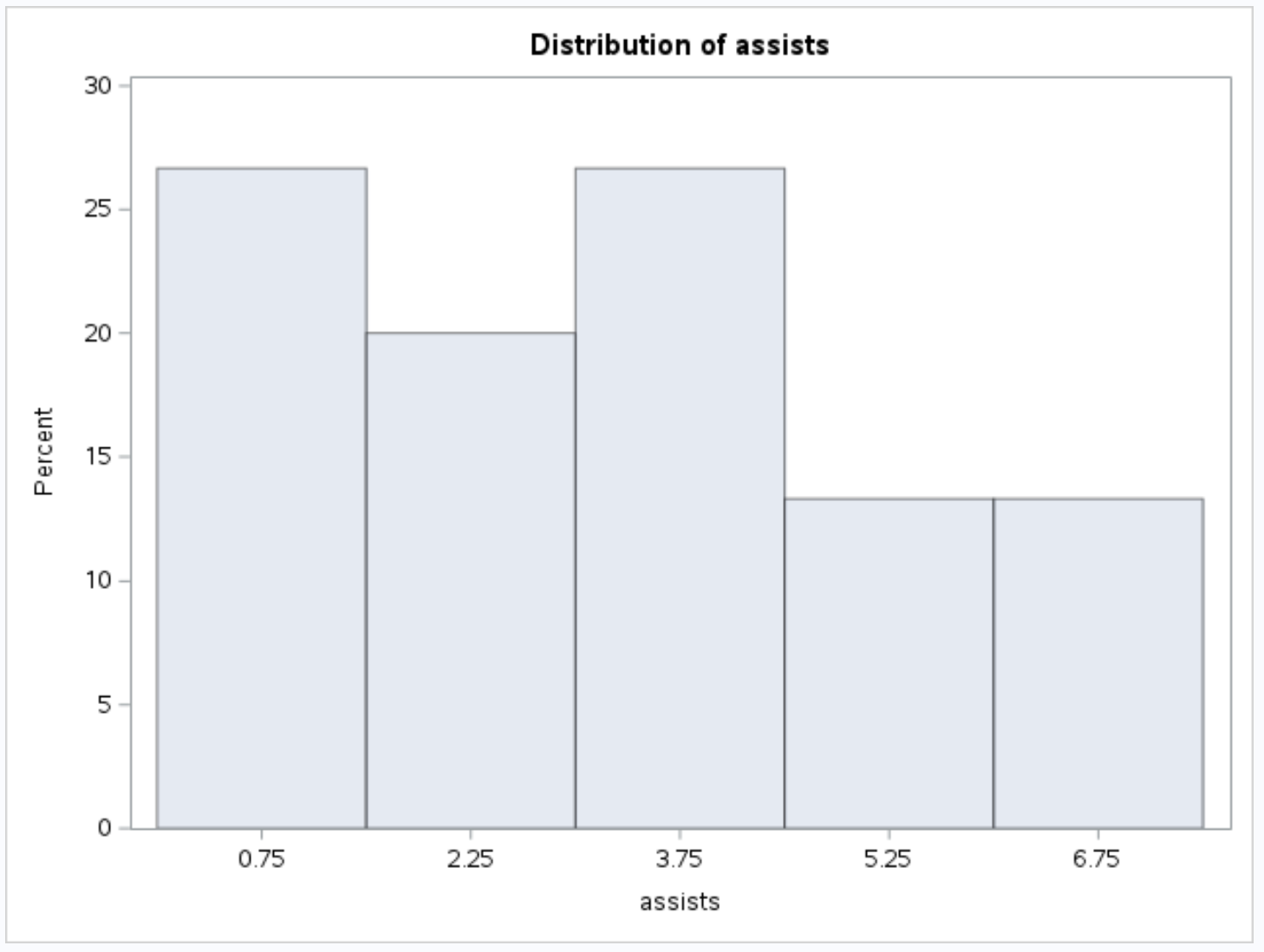
Zusätzliche Ressourcen
In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:
So berechnen Sie deskriptive Statistiken in SAS
So erstellen Sie Häufigkeitstabellen in SAS
So berechnen Sie Perzentile in SAS
So erstellen Sie PivotTables in SAS