So führen sie eine hauptkomponentenanalyse in sas durch

Die Hauptkomponentenanalyse (PCA) ist eine unbeaufsichtigte Technik des maschinellen Lernens, die versucht, die Hauptkomponenten – lineare Kombinationen von Prädiktorvariablen – zu finden, die einen großen Teil der Variation in einem Datensatz erklären.

Der einfachste Weg, PCA in SAS durchzuführen, ist die Verwendung der PROC PRINCOMP- Anweisung, die die folgende grundlegende Syntax verwendet:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

Hier erfahren Sie, was jede Anweisung bewirkt:

• data : Der Name des Datensatzes, der für die PCA verwendet werden soll
• out : Der Name des zu erstellenden Datensatzes, der alle Originaldaten sowie die Hauptkomponentenwerte enthält
• outstat : Gibt an, dass ein Datensatz erstellt werden soll, der Mittelwerte, Standardabweichungen, Korrelationskoeffizienten, Eigenwerte und Eigenvektoren enthält.
• var : die für PCA zu verwendenden Variablen aus dem Eingabedatensatz.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie die PROC PRINCOMP- Anweisung in der Praxis verwenden, um eine Hauptkomponentenanalyse in SAS durchzuführen.

Schritt 1: Erstellen Sie einen Datensatz

Angenommen, wir haben den folgenden Datensatz, der verschiedene Informationen über 20 Basketballspieler enthält:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

Schritt 2: Führen Sie eine Hauptkomponentenanalyse durch

Wir können die PROC PRINCOMP- Anweisung verwenden, um eine Hauptkomponentenanalyse unter Verwendung der Punkte- , Assists- und Bounces -Variablen des Datensatzes durchzuführen:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

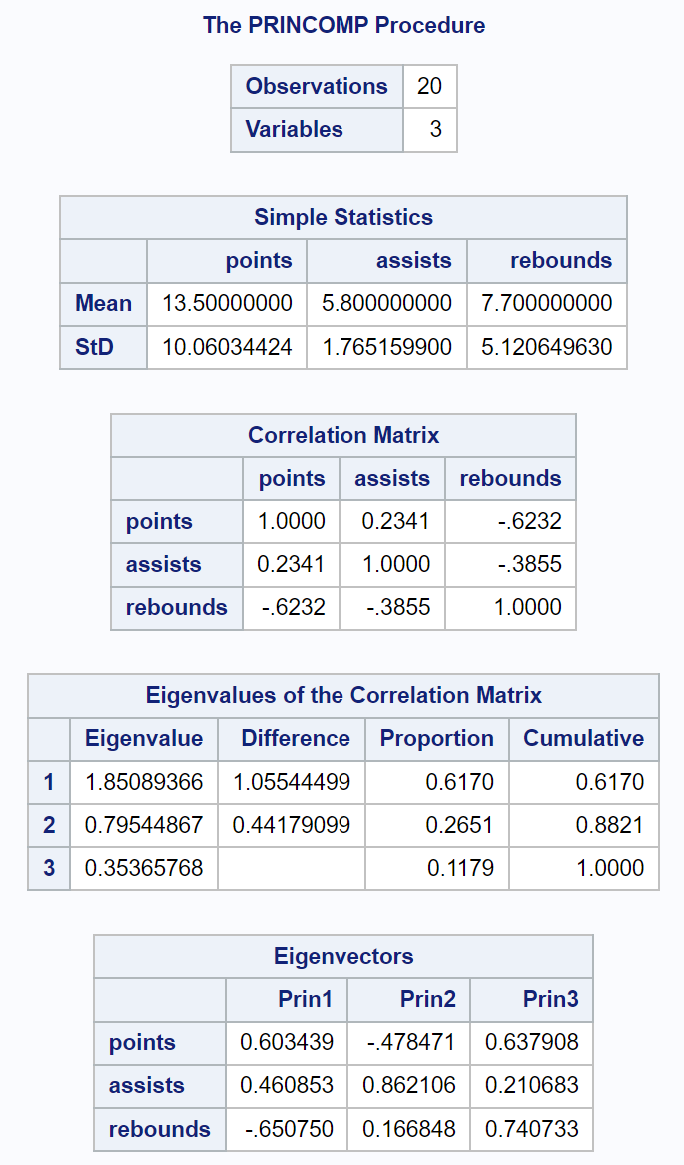
Der erste Teil der Ausgabe zeigt verschiedene deskriptive Statistiken an, darunter den Mittelwert und die Standardabweichung jeder Eingabevariablen, eine Korrelationsmatrix sowie die Werte der Eigenwerte und Eigenvektoren:

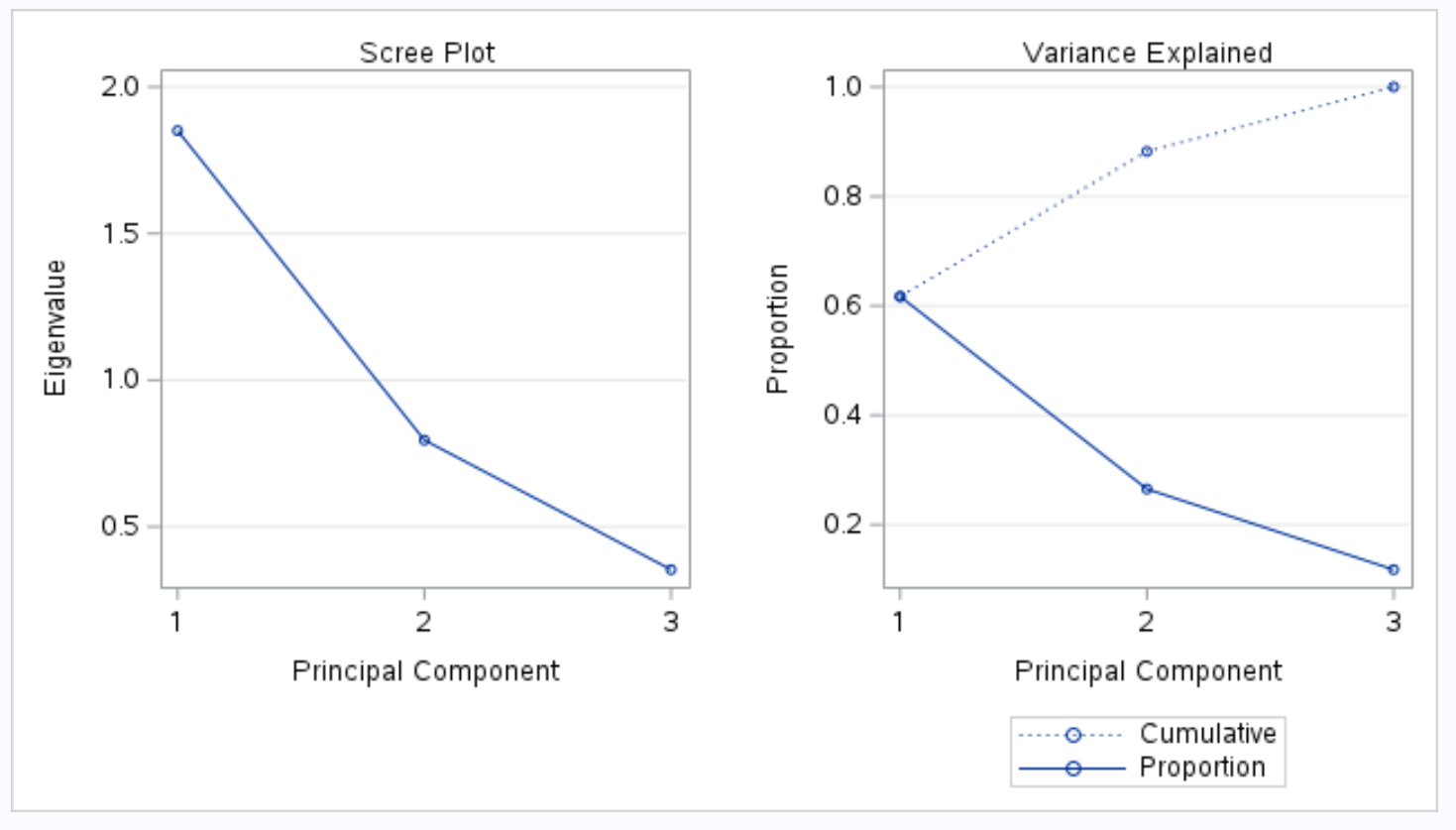
Der nächste Teil der Ausgabe zeigt ein Gerölldiagramm und ein erklärtes Varianzdiagramm :

Wenn wir PCA durchführen, möchten wir oft verstehen, wie viel Prozent der Gesamtvariation im Datensatz durch jede Hauptkomponente erklärt werden kann.

Die resultierende Tabelle mit dem Titel Korrelationsmatrix-Eigenwerte ermöglicht es uns, genau zu sehen, welcher Prozentsatz der Gesamtvariation durch jede Hauptkomponente erklärt wird:

• Die erste Hauptkomponente erklärt 61,7 % der Gesamtvariation im Datensatz.
• Die zweite Hauptkomponente erklärt 26,51 % der Gesamtvariation im Datensatz.
• Die dritte Hauptkomponente erklärt 11,79 % der Gesamtvariation im Datensatz.

Beachten Sie, dass sich alle Prozentangaben zu 100 % addieren.

Der Plot mit dem Titel „Varianz erklärt“ ermöglicht es uns dann, diese Werte zu visualisieren.

Die x-Achse zeigt die Hauptkomponente und die y-Achse den Prozentsatz der Gesamtvarianz, der durch jede einzelne Hauptkomponente erklärt wird.

Schritt 3: Erstellen Sie einen Biplot, um die Ergebnisse zu visualisieren

Um die PCA-Ergebnisse für einen bestimmten Datensatz zu visualisieren, können wir einen Biplot erstellen, bei dem es sich um einen Plot handelt, der jede Beobachtung in einem Datensatz auf einer Ebene anzeigt, die durch die ersten beiden Hauptkomponenten gebildet wird.

Wir können in SAS die folgende Syntax verwenden, um einen Biplot zu erstellen:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

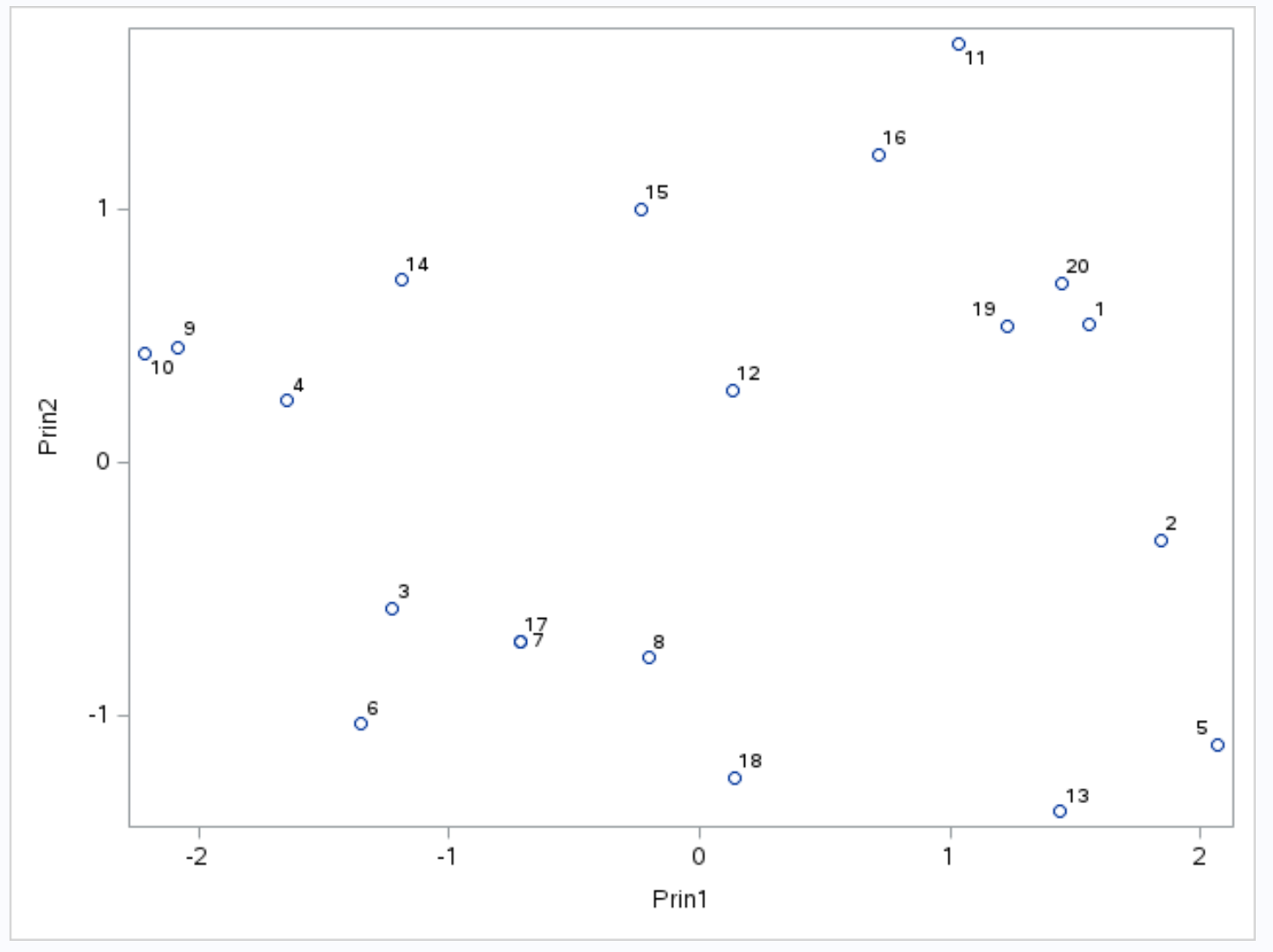
Die x-Achse zeigt die erste Hauptkomponente, die y-Achse die zweite Hauptkomponente und einzelne Beobachtungen aus dem Datensatz werden im Diagramm als kleine Kreise angezeigt.

Die in der Grafik nebeneinander stehenden Beobachtungen haben ähnliche Werte für die drei Variablen Punkte , Assists und Rebounds .

Ganz links im Diagramm können wir beispielsweise sehen, dass die Beobachtungen Nr. 9 und Nr. 10 extrem nahe beieinander liegen.

Wenn wir uns auf den Originaldatensatz beziehen, können wir die folgenden Werte für diese Beobachtungen sehen:

• Beobachtung Nr. 9 : 2 Punkte, 5 Assists, 17 Rebounds
• Beobachtung Nr. 10 : 4 Punkte, 5 Assists, 19 Rebounds

Die Werte sind für jede der drei Variablen ähnlich, was erklärt, warum diese Beobachtungen im Biplot so nahe beieinander liegen.

Wir haben auch in der Ergebnistabelle mit dem Titel Korrelationsmatrix-Eigenwerte gesehen, dass die ersten beiden Hauptkomponenten 88,21 % der Gesamtvariation im Datensatz ausmachen.

Da dieser Prozentsatz sehr hoch ist, ist es sinnvoll zu analysieren, welche Beobachtungen im Biplot nahe beieinander liegen, da die beiden Hauptkomponenten, aus denen der Biplot besteht, fast die gesamte Variation im Datensatz ausmachen.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:

So führen Sie eine einfache lineare Regression in SAS durch
So führen Sie eine multiple lineare Regression in SAS durch
So führen Sie eine logistische Regression in SAS durch