Statistische bevölkerung

In diesem Artikel erklären wir, was eine statistische Grundgesamtheit ist. Sie finden mehrere Beispiele für statistische Grundgesamtheiten, die verschiedenen Arten von Grundgesamtheiten, die es gibt, und schließlich, was der Unterschied zwischen Grundgesamtheit und Stichprobe in der Statistik ist.

Was ist eine statistische Grundgesamtheit?

In der Statistik ist eine Grundgesamtheit eine Menge von Elementen mit ähnlichen Merkmalen, an denen eine statistische Studie durchgeführt werden soll.

Dieses Konzept kann austauschbar als statistische Bevölkerung oder einfach Bevölkerung bezeichnet werden.

Als nächstes ist die Populationsgröße , auch Populationsgröße genannt, die Gesamtzahl der Elemente in der Gruppe, die Sie untersuchen möchten.

Beispiele für statistische Bevölkerung

Betrachten wir die Definition der statistischen Grundgesamtheit, sehen wir uns mehrere Beispiele für Grundgesamtheiten an, um deren Bedeutung besser zu verstehen.

Wenn wir beispielsweise eine Studie über die Noten durchführen, die Schüler einer Klasse im Laufe eines Jahres erhalten, bilden die Schüler dieser Klasse die statistische Grundgesamtheit der Studie.

Ein weiteres Beispiel: Wenn Sie eine statistische Analyse der Qualität der in einer Fabrik in einem bestimmten Zeitraum hergestellten Teile durchführen möchten, bilden alle von dieser Fabrik in diesem Zeitraum hergestellten Teile die untersuchte Population.

Schließlich sind die Einwohner eines Territoriums auch dann eine statistische Grundgesamtheit, wenn Statistiken über dieses Gebiet durchgeführt werden, wie beispielsweise bei der Berechnung der Lebenserwartung eines Landes, wobei die Einwohner dieses Landes die statistische Grundgesamtheit der Studie darstellen.

Arten der statistischen Bevölkerung

Es gibt zwei Arten von statistischen Grundgesamtheiten:

• Endliche statistische Grundgesamtheit : Grundgesamtheit, deren Anzahl Elemente endlich ist, d. h. sie können gezählt werden.
• Unendliche statistische Population : Population, deren Anzahl an Elementen unendlich ist, d. h. die kein Ende hat.

Beispielsweise stellt die Anzahl der Autos, die an einem Tag auf einer Straße fahren, eine endliche Bevölkerung dar, da sie, selbst wenn es sich um eine sehr große Zahl handelt, zählbar ist. Stattdessen stellt die Anzahl der Planeten im Universum eine unendliche Population dar, da noch nicht alle Planeten entdeckt wurden und daher nicht gezählt werden können.

Sie sollten bedenken, dass es viele Möglichkeiten gibt, statistische Populationstypen zu gruppieren. Sie können anhand ihrer Variablen auch in qualitative Populationen und quantitative Populationen unterteilt werden. Normalerweise wird jedoch eine große Klassifizierung zwischen endlichen Populationen und unendlichen Populationen vorgenommen.

Statistische Grundgesamtheit und Stichprobe

Abschließend werden wir sehen, wie sich die Begriffe „Grundgesamtheit“ und „Stichprobe“ in der Statistik unterscheiden, da es sich um zwei Begriffe handelt, die im Allgemeinen Hand in Hand gehen.

In der Statistik ist die Differenz zwischen Grundgesamtheit und Stichprobe der Anteil relativ zur Gesamtzahl der Elemente in der Studie. Die statistische Grundgesamtheit umfasst alle Elemente, an denen die Studie durchgeführt wird. Die statistische Stichprobe ist jedoch Teil aller Elemente der Studie.

Die Größe einer Stichprobe wird daher immer kleiner oder gleich der Größe einer Grundgesamtheit sein.

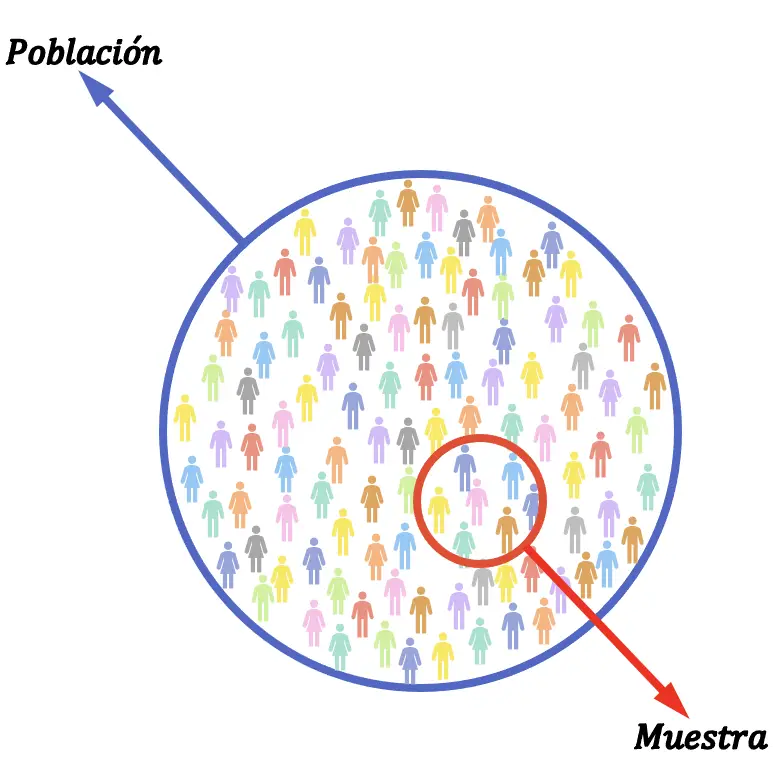
Die statistische Stichprobe kann auch als Teilmenge der Grundgesamtheit bezeichnet werden.

Um eine Population statistisch zu untersuchen, werden normalerweise nicht Daten von jedem Element der Population entnommen, sondern es wird eine repräsentative Stichprobe ausgewählt, die Studie wird an dieser Stichprobe durchgeführt und die Ergebnisse werden dann auf die gesamte Population extrapoliert. Bevölkerung.

Wenn Sie beispielsweise Marktforschung betreiben möchten, befragen Sie nicht jeden, der sich für Ihr Produkt interessiert, sondern befragen nur einen Teil und untersuchen mit den gesammelten Daten den Markt.

Es ist zu beachten, dass die Stichprobengröße (Stichprobengröße) einer statistischen Studie nicht trivial zu bestimmen ist, denn je größer die Stichprobengröße, desto besser repräsentiert sie die Grundgesamtheit, aber je größer die Stichprobengröße, desto komplizierter ist die Analyse wird sein. und daher werden mehr Ressourcen und mehr Geld benötigt.