Beschreibende oder inferenzielle statistik: was ist der unterschied?

Im Bereich der Statistik gibt es zwei Hauptzweige:

• Beschreibende Statistik
• Inferenzstatistik

Dieses Tutorial erklärt den Unterschied zwischen den beiden Zweigen und warum jeder in bestimmten Situationen nützlich ist.

Beschreibende Statistik

Kurz gesagt zielt die deskriptive Statistik darauf ab, eine Reihe von Rohdaten mithilfe zusammenfassender Statistiken, Grafiken und Tabellen zu beschreiben .

Beschreibende Statistiken sind nützlich, weil sie es Ihnen ermöglichen, eine Datengruppe viel schneller und einfacher zu verstehen, als wenn Sie nur zeilenweise Rohdatenwerte betrachten.

Nehmen wir zum Beispiel an, wir haben einen Rohdatensatz, der die Testergebnisse von 1.000 Schülern einer bestimmten Schule zeigt. Für uns könnten sowohl das durchschnittliche Testergebnis als auch die Verteilung der Testergebnisse von Interesse sein.

Mithilfe deskriptiver Statistiken könnten wir die durchschnittliche Punktzahl ermitteln und ein Diagramm erstellen, das uns dabei hilft, die Verteilung der Punktzahlen zu visualisieren.

Dies ermöglicht es uns, die Testergebnisse der Schüler viel einfacher zu verstehen, als nur die Rohdaten zu betrachten.

Gängige Formen der deskriptiven Statistik

Es gibt drei gängige Formen der deskriptiven Statistik:

1. Zusammenfassende Statistiken. Dabei handelt es sich um Statistiken, die Daten anhand einer einzigen Zahl zusammenfassen . Es gibt zwei gängige Arten von zusammenfassenden Statistiken:

• Maße der zentralen Tendenz : Diese Zahlen beschreiben, wo sich das Zentrum eines Datensatzes befindet. Beispiele hierfür sind Durchschnitt   und der Median .
• Streuungsmaße: Diese Zahlen beschreiben die Verteilung der Werte im Datensatz. Beispiele hierfür sind Intervall , Interquartilbereich , Standardabweichung und Varianz .

2. Grafiken . Diagramme helfen uns, Daten zu visualisieren. Zu den gängigen Diagrammtypen zur Visualisierung von Daten gehören Boxplots , Histogramme , Stamm- und Blattdiagramme sowieStreudiagramme .

3. Tabellen . Tabellen können uns helfen zu verstehen, wie Daten verteilt sind. Ein gängiger Tabellentyp ist die Häufigkeitstabelle , die uns sagt, wie viele Datenwerte in bestimmte Bereiche fallen.

Beispiel für die Verwendung deskriptiver Statistiken

Das folgende Beispiel veranschaulicht, wie wir deskriptive Statistiken in der realen Welt verwenden könnten.

Es wird davon ausgegangen, dass 1.000 Schüler einer bestimmten Schule alle denselben Test absolvieren. Wir möchten die Verteilung der Testergebnisse verstehen und verwenden daher die folgenden deskriptiven Statistiken:

1. Zusammenfassende Statistiken

Durchschnitt: 82,13 . Daraus ergibt sich, dass das durchschnittliche Testergebnis unter den 1.000 Studierenden 82,13 beträgt.

Median: 84. Dies zeigt uns, dass die Hälfte aller Schüler über 84 und die andere Hälfte unter 84 punktete.

Max: 100. Min: 45. Dies sagt uns, dass die maximale Punktzahl, die ein Schüler erreichte, 100 und die minimale Punktzahl 45 betrug. Der Bereich – der uns die Differenz zwischen dem Maximum und dem Minimum angibt – beträgt 55.

2. Grafiken

Um die Verteilung der Testergebnisse zu visualisieren, können wir ein Histogramm erstellen – eine Art Diagramm, das rechteckige Balken zur Darstellung von Häufigkeiten verwendet.

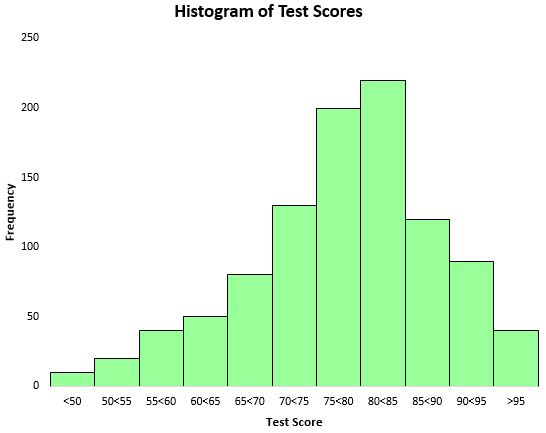
Anhand dieses Histogramms können wir erkennen, dass die Verteilung der Testergebnisse ungefähr glockenförmig ist. Die meisten Schüler erzielten eine Punktzahl zwischen 70 und 90, während nur sehr wenige über 95 und noch weniger unter 50 punkteten.

3. Tabellen

Eine weitere einfache Möglichkeit, die Verteilung der Bewertungen zu verstehen, ist die Erstellung einer Häufigkeitstabelle. Die folgende Häufigkeitstabelle zeigt beispielsweise den Prozentsatz der Schüler, die in verschiedenen Bereichen punkteten:

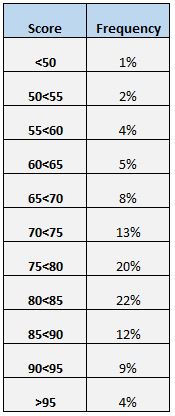
Wir können sehen, dass nur 4 % aller Schüler über 95 Punkte erzielten. Wir können auch sehen, dass (12 % + 9 % + 4 % = ) 25 % aller Schüler 85 Punkte oder mehr erzielten.

Eine Häufigkeitstabelle ist besonders nützlich, wenn wir wissen möchten, wie viel Prozent der Datenwerte über oder unter einem bestimmten Wert liegen. Angenommen, die Schule betrachtet ein „akzeptables“ Testergebnis als ein Ergebnis über 75.

Wenn wir uns die Häufigkeitstabelle ansehen, können wir leicht erkennen, dass (20 % + 22 % + 12 % + 9 % + 4 % =) 67 % der Schüler im Test eine akzeptable Punktzahl erzielten.

Inferenzstatistik

Kurz gesagt: Die Inferenzstatistik verwendet eine kleine Datenstichprobe, um Rückschlüsse auf die größere Population zu ziehen, aus der die Stichprobe gezogen wird.

Beispielsweise möchten wir vielleicht die politischen Vorlieben von Millionen Menschen in einem Land verstehen.

Es wäre jedoch zu zeitaufwändig und teuer, jeden Einzelnen im Land zu befragen. Stattdessen würden wir eine kleinere Umfrage unter beispielsweise 1.000 Amerikanern durchführen und anhand der Umfrageergebnisse Rückschlüsse auf die Bevölkerung als Ganzes ziehen.

Dies ist die gesamte Prämisse der Inferenzstatistik: Wir möchten eine Frage zu einer Population beantworten, also erhalten wir Daten für eine kleine Stichprobe dieser Population und verwenden die Stichprobendaten, um Rückschlüsse auf die Population zu ziehen.

Die Bedeutung einer repräsentativen Stichprobe

Um sicher zu sein, dass wir anhand einer Stichprobe Rückschlüsse auf eine Population ziehen können, müssen wir sicherstellen, dass wir über eine repräsentative Stichprobe verfügen, d Eigenschaften. der Gesamtbevölkerung.

Im Idealfall möchten wir, dass unsere Stichprobe einer „Miniversion“ unserer Grundgesamtheit ähnelt. Wenn wir also Rückschlüsse auf eine Schülerpopulation ziehen wollen, die zu 50 % aus Mädchen und zu 50 % aus Jungen besteht, wäre unsere Stichprobe nicht repräsentativ, wenn sie 90 % Jungen und nur 10 % Mädchen umfassen würde.

Wenn unsere Stichprobe nicht der Gesamtbevölkerung ähnelt, können wir die Ergebnisse der Stichprobe nicht sicher auf die Gesamtbevölkerung übertragen.

So erhalten Sie eine repräsentative Stichprobe

Um die Chancen auf eine repräsentative Stichprobe zu maximieren, sollten Sie sich auf zwei Dinge konzentrieren:

1. Stellen Sie sicher, dass Sie eine Zufallsstichprobenmethode verwenden.

Es gibt mehrere Zufallsstichprobenmethoden , mit denen Sie wahrscheinlich eine repräsentative Stichprobe erstellen können, darunter:

• Eine einfache Zufallsstichprobe
• Eine systematische Zufallsstichprobe
• Eine Cluster-Zufallsstichprobe
• Eine geschichtete Zufallsstichprobe

Zufallsstichprobenverfahren führen in der Regel zu repräsentativen Stichproben, da jedes Mitglied der Bevölkerung die gleiche Chance hat, in die Stichprobe aufgenommen zu werden.

2. Stellen Sie sicher, dass Ihre Stichprobe groß genug ist .

Neben der Verwendung einer geeigneten Stichprobenmethode ist es wichtig sicherzustellen, dass die Stichprobe groß genug ist, damit Sie über genügend Daten verfügen, um eine Verallgemeinerung auf eine größere Grundgesamtheit durchführen zu können.

Um Ihre Stichprobengröße zu bestimmen, müssen Sie die Größe der Population, die Sie untersuchen, das Konfidenzniveau, das Sie verwenden möchten, und die Fehlermarge, die Sie für akzeptabel halten, berücksichtigen.

Glücklicherweise können Sie Online-Rechner verwenden, um diese Werte einzugeben und zu sehen, wie groß Ihre Stichprobe sein sollte.

Gängige Formen der Inferenzstatistik

Es gibt drei gängige Formen der Inferenzstatistik:

1. Hypothesentest.

Wir möchten oft Fragen zu einer Bevölkerung beantworten wie:

• Ist der Prozentsatz der Menschen in Ohio, die Kandidat A unterstützen, größer als 50 %?
• Entspricht die durchschnittliche Höhe einer bestimmten Pflanze 14 Zoll?
• Gibt es einen Unterschied zwischen der durchschnittlichen Körpergröße der Schüler von Schule A und Schule B?

Um diese Fragen zu beantworten, können wir Hypothesentests durchführen, die es uns ermöglichen, Daten aus einer Stichprobe zu verwenden, um Rückschlüsse auf Populationen zu ziehen.

2. Konfidenzintervalle .

Manchmal möchten wir einen bestimmten Wert für eine Population schätzen. Beispielsweise könnte uns die durchschnittliche Höhe einer bestimmten Pflanzenart in Australien interessieren.

Anstatt jede Pflanze im Land zu vermessen, könnten wir eine kleine Pflanzenprobe sammeln und jede einzelne vermessen. Dann können wir die durchschnittliche Höhe der Pflanzen in der Stichprobe verwenden, um die durchschnittliche Höhe der Population abzuschätzen.

Es ist jedoch unwahrscheinlich, dass unsere Stichprobe eine perfekte Bevölkerungsschätzung liefert. Glücklicherweise können wir dieser Unsicherheit Rechnung tragen, indem wir einKonfidenzintervall erstellen, das einen Wertebereich bereitstellt, innerhalb dessen wir sicher sind, dass der wahre Populationsparameter liegt.

Beispielsweise könnten wir ein 95 %-Konfidenzintervall von [13,2, 14,8] erstellen, was bedeutet, dass wir zu 95 % sicher sind, dass die tatsächliche durchschnittliche Höhe dieser Pflanzenart zwischen 13,2 Zoll und 14,8 Zoll liegt.

3. Regression .

Manchmal möchten wir die Beziehung zwischen zwei Variablen in einer Population verstehen.

Nehmen wir zum Beispiel an, wir möchten wissen, ob die Lernstunden pro Woche mit den Testergebnissen zusammenhängen. Um diese Frage zu beantworten, könnten wir eine Technik namensRegressionsanalyse durchführen.

Wir können uns also die Anzahl der gelernten Stunden sowie die Testergebnisse von 100 Schülern ansehen und eine Regressionsanalyse durchführen, um zu sehen, ob zwischen den beiden Variablen ein signifikanter Zusammenhang besteht.

Wenn sich herausstellt, dass der p-Wert der Regression signifikant ist , können wir daraus schließen, dass zwischen diesen beiden Variablen in der gesamten Studierendenpopulation ein signifikanter Zusammenhang besteht.

Der Unterschied zwischen deskriptiver und inferenzieller Statistik

Zusammenfassend lässt sich der Unterschied zwischen deskriptiver und inferenzieller Statistik wie folgt beschreiben:

Beschreibende Statistiken verwenden zusammenfassende Statistiken, Grafiken und Tabellen, um einen Datensatz zu beschreiben .

Dies ist nützlich, um einen Datensatz schnell und einfach zu verstehen, ohne alle einzelnen Datenwerte durchgehen zu müssen.

Inferenzstatistiken nutzen Stichproben, um Rückschlüsse auf größere Populationen zu ziehen.

Abhängig von der Frage, die Sie zu einer Population beantworten möchten, können Sie sich für eine oder mehrere der folgenden Methoden entscheiden: Hypothesentests, Konfidenzintervalle und Regressionsanalyse.

Wenn Sie sich für eine dieser Methoden entscheiden, denken Sie daran, dass Ihre Stichprobe repräsentativ für Ihre Grundgesamtheit sein muss , da die von Ihnen gezogenen Schlussfolgerungen sonst nicht zuverlässig sind.