So ermitteln sie einen p-wert aus einem z-wert in excel

Viele Hypothesentests in der Statistik führen zu einer Z-Test-Statistik. Sobald wir diese Z-Test-Statistik gefunden haben, finden wir normalerweise den damit verbundenen p-Wert. Wenn dieser p-Wert unter einem bestimmten Alpha-Wert liegt (z. B. 0,10, 0,05, 0,01), lehnen wir die Nullhypothese des Tests ab und kommen zu dem Schluss, dass unsere Ergebnisse signifikant sind.

Dieses Tutorial zeigt mehrere Beispiele für die Ermittlung des p-Werts aus einem Z-Score in Excel mithilfe der Funktion NORM.VERT , die die folgenden Argumente verwendet:

NORM.VERT (x, Durchschnitt, Standard_Abteilung, kumulativ)

Gold:

• x ist der z-Score, der uns interessiert.
• Mittelwert ist der Mittelwert der Verteilung – wir verwenden „0“ für die Standardnormalverteilung.
• standard_dev ist die Standardabweichung der Verteilung – wir verwenden „1“ für die Standardnormalverteilung.
• kumulativ nimmt den Wert „TRUE“ (gibt die CDF zurück) oder „FALSE“ (gibt das PDF zurück) an – wir verwenden „TRUE“, um den Wert der kumulativen Verteilungsfunktion zu erhalten.

Sehen wir uns einige Beispiele an.

Beispiel 1: Ermitteln eines P-Werts aus einem Z-Score (zweiseitiger Test)

Ein Unternehmen möchte wissen, ob ein neuer Batterietyp eine andere durchschnittliche Lebensdauer hat als die aktuelle Standardbatterie, die eine durchschnittliche Lebensdauer von 18 Stunden hat. In einer Stichprobe von 100 neuen Batterien stellten sie fest, dass die durchschnittliche Lebensdauer 19 Stunden beträgt, mit einer Standardabweichung von 4 Stunden.

Führen Sie einen zweiseitigen Hypothesentest mit einem Alpha-Wert von 0,05 durch, um festzustellen, ob sich die durchschnittliche Lebensdauer der neuen Batterie von der durchschnittlichen Lebensdauer der aktuellen Standardbatterie unterscheidet.

Schritt 1: Formulieren Sie die Hypothesen.

Die Nullhypothese (H ₀ ): μ = 18

Die Alternativhypothese: (Ha): μ ≠ 18

Schritt 2: Finden Sie die Z-Test-Statistik.

Teststatistik z = (x-μ) / (s/√n) = (19-18) / (4/√100) = 2,5

Schritt 3: Ermitteln Sie den p-Wert der Z-Test-Statistik mit Excel.

Um den p-Wert für z = 2,5 zu ermitteln, verwenden wir die folgende Formel in Excel: =1 – NORM.DIST(2,5, 0, 1, TRUE)

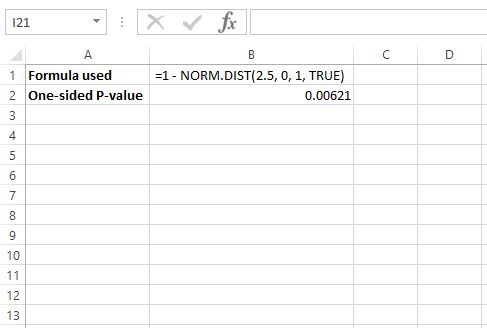
Dies sagt uns, dass der einseitige p-Wert .00621 beträgt, aber da wir einen zweiseitigen Test durchführen, müssen wir diesen Wert mit 2 multiplizieren, sodass der p-Wert .00612 * 2 = .01224 beträgt.

Schritt 4: Lehnen Sie die Nullhypothese ab oder lehnen Sie sie nicht ab.

Da der p-Wert von 0,01224 kleiner als der gewählte Alpha-Wert von 0,05 ist, lehnen wir die Nullhypothese ab. Wir haben genügend Beweise dafür, dass sich die durchschnittliche Lebensdauer der neuen Batterie erheblich von der durchschnittlichen Lebensdauer der aktuellen Standardbatterie unterscheidet.

Beispiel 2: Ermitteln eines P-Werts aus einem Z-Score (einseitiger Test)

Ein Botaniker schätzt, dass die durchschnittliche Höhe einer bestimmten Pflanze weniger als 14 Zoll beträgt. Sie wählt zufällig 30 Pflanzen aus und misst sie. Sie stellt fest, dass die durchschnittliche Körpergröße 13,5 Zoll beträgt, mit einer Standardabweichung von 2 Zoll.

Führen Sie einen einseitigen Hypothesentest mit einem Alpha-Wert von 0,01 durch, um festzustellen, ob die durchschnittliche Höhe dieser Pflanze tatsächlich weniger als 14 Zoll beträgt.

Schritt 1: Formulieren Sie die Hypothesen.

Die Nullhypothese (H0): μ≥ 14

Die Alternativhypothese: (Ha): μ < 14

Schritt 2: Finden Sie die Z-Test-Statistik.

Teststatistik z = (x-μ) / (s/√n) = (13,5-14) / (2/√30) = -1,369

Schritt 3: Ermitteln Sie den p-Wert der Z-Test-Statistik mit Excel.

Um den p-Wert für z = -1,369 zu ermitteln, verwenden wir die folgende Formel in Excel: =NORM.VERT(-1,369, 0, 1, WAHR)

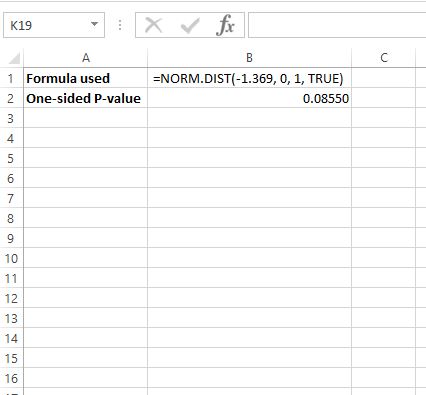
Dies sagt uns, dass der einseitige p-Wert 0,08550 beträgt.

Schritt 4: Lehnen Sie die Nullhypothese ab oder lehnen Sie sie nicht ab.

Da der p-Wert von 0,08550 größer ist als der gewählte Alpha-Wert von 0,01 , können wir die Nullhypothese nicht ablehnen. Wir haben nicht genügend Beweise dafür, dass die durchschnittliche Höhe dieser Pflanzenart weniger als 14 Zoll beträgt.

Weitere Tutorials zu Statistiken in Excel finden Sie in unserer vollständigen Liste der Excel-Anleitungen .