Wird der interquartilbereich (iqr) durch ausreißer beeinflusst?

In der Statistik möchten wir oft wissen, wie weit Werte in einer Verteilung „verteilt“ sind.

Eine beliebte Methode zur Messung der Streuung ist der Interquartilbereich , der als Differenz zwischen dem ersten Quartil und dem dritten Quartil eines Datensatzes berechnet wird. Quartile sind einfach Werte, die einen Datensatz in vier gleiche Teile teilen.

Beispiel: Berechnung des Interquartilbereichs

Das folgende Beispiel zeigt, wie der Interquartilbereich für einen bestimmten Datensatz berechnet wird:

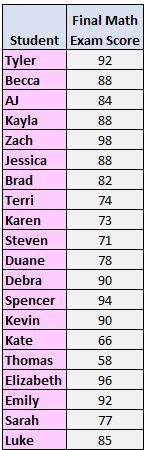
Schritt 1: Ordnen Sie die Werte vom kleinsten zum größten.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. Finden Sie den Median.

58, 66, 71, 73, 74, 77 , 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

In diesem Fall liegt der Median zwischen 85 und 88.

3. Der Median teilt den Datensatz in zwei Hälften. Der Median der unteren Hälfte ist das untere Quartil und der Median der oberen Hälfte ist das obere Quartil:

58, 66, 71 , 73, 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. Berechnen Sie den Interquartilbereich.

In diesem Fall ist das erste Quartil der Durchschnitt der beiden mittleren Werte in der unteren Hälfte des Datensatzes (75,5) und das dritte Quartil ist der Durchschnitt der beiden mittleren Werte in der oberen Hälfte des Datensatzes (91).

Der Interquartilbereich beträgt also 91 – 75,5 = 15,5

Der Interquartilbereich wird durch Ausreißer nicht beeinflusst

Einer der Gründe, warum Menschen den Interquartilbereich (IQR) bei der Berechnung der „Spreizung“ eines Datensatzes bevorzugen, ist seine Robustheit gegenüber Ausreißern. Da es sich beim IQR einfach um den mittleren 50 %-Bereich der Datenwerte handelt, wird er nicht durch extreme Ausreißer beeinflusst.

Um dies zu veranschaulichen, betrachten Sie den folgenden Datensatz:

[1, 4, 8, 11, 13, 17, 17, 20]

Hier sind die verschiedenen Ausbreitungsmetriken für diesen Datensatz:

• Interquartilbereich: 11
• Bereich: 19
• Standardabweichung: 6,26
• Differenz: 39,23

Betrachten Sie nun denselben Datensatz, jedoch mit einem zusätzlichen extremen Ausreißer:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

Hier sind die verschiedenen Ausbreitungsmetriken für diesen Datensatz:

• Interquartilbereich: 12,5
• Bereich: 149
• Standardabweichung: 43,96
• Spread: 1.932,84

Beachten Sie, dass sich der Interquartilbereich nur geringfügig von 11 auf 12,5 ändert. Alle anderen Streuungsmaße ändern sich jedoch dramatisch.

Dies zeigt, dass der Interquartilbereich nicht wie andere Streuungsmaße von Ausreißern beeinflusst wird. Aus diesem Grund ist es eine zuverlässige Methode, die Verteilung der mittleren 50 % der Werte in jeder Verteilung zu messen.

Weiterführende Literatur:

Ausbreitungsmessungen
Interquartilbereichsrechner