So führen sie einen mann-whitney-u-test in excel durch

Ein Mann-Whitney-U-Test (manchmal auch Wilcoxon-Rangsummentest genannt) wird verwendet, um Unterschiede zwischen zwei Stichproben zu vergleichen, wenn die Stichprobenverteilungen nicht normalverteilt sind und die Stichprobengrößen klein sind (n < 30).

Er gilt als nichtparametrisches Äquivalent des t-Tests bei zwei Stichproben .

In diesem Tutorial wird erläutert, wie Sie einen Mann-Whitney-U-Test in Excel durchführen.

Beispiel: Mann-Whitney-U-Test in Excel

Forscher möchten wissen, ob die Kraftstoffaufbereitung zu einer Veränderung des durchschnittlichen Kraftstoffverbrauchs eines Autos führt. Um dies zu testen, führen sie ein Experiment durch, bei dem sie den mpg von 12 Autos mit Kraftstoffaufbereitung und 12 Autos ohne Aufbereitung messen.

Da die Stichprobengrößen klein sind und sie vermuten, dass die Stichprobenverteilungen nicht normalverteilt sind, beschlossen sie, einen Mann-Whitney-U-Test durchzuführen, um festzustellen, ob zwischen den beiden Gruppen ein statistisch signifikanter Unterschied in mpg besteht.

Führen Sie die folgenden Schritte aus, um einen Mann-Whitney-U-Test in Excel durchzuführen.

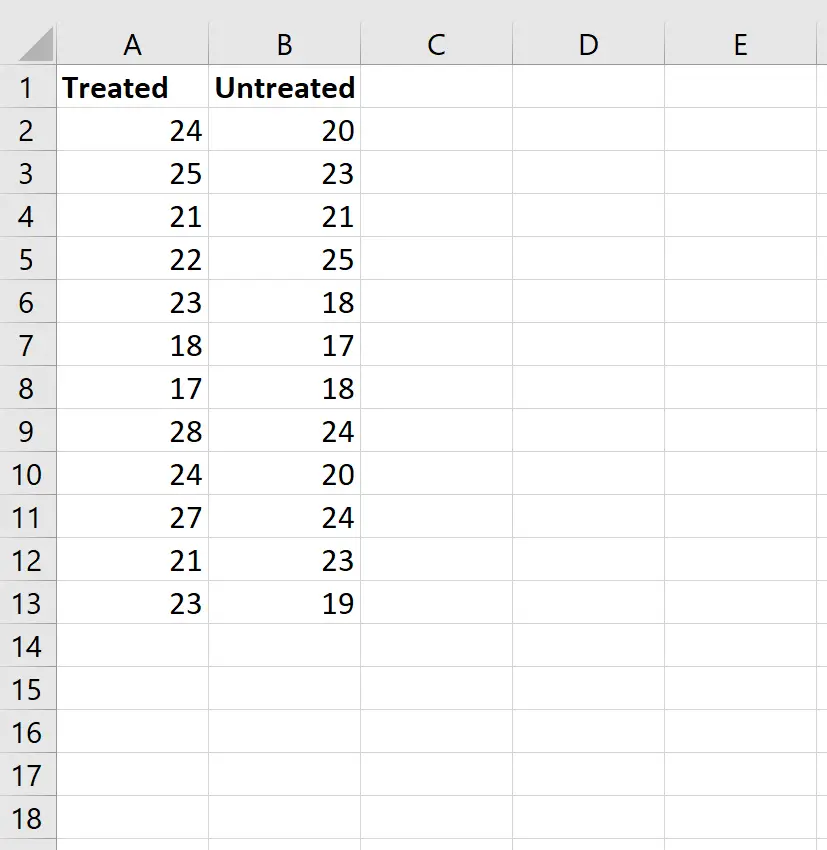
Schritt 1: Geben Sie die Daten ein.

Geben Sie die Daten wie folgt ein:

Schritt 2: Berechnen Sie die Rangfolge für beide Gruppen.

Als nächstes berechnen wir die Platzierungen für jede Gruppe. Das folgende Bild zeigt die Formel zur Berechnung des Rangs des ersten Werts in der Gruppe „Verarbeitet“:

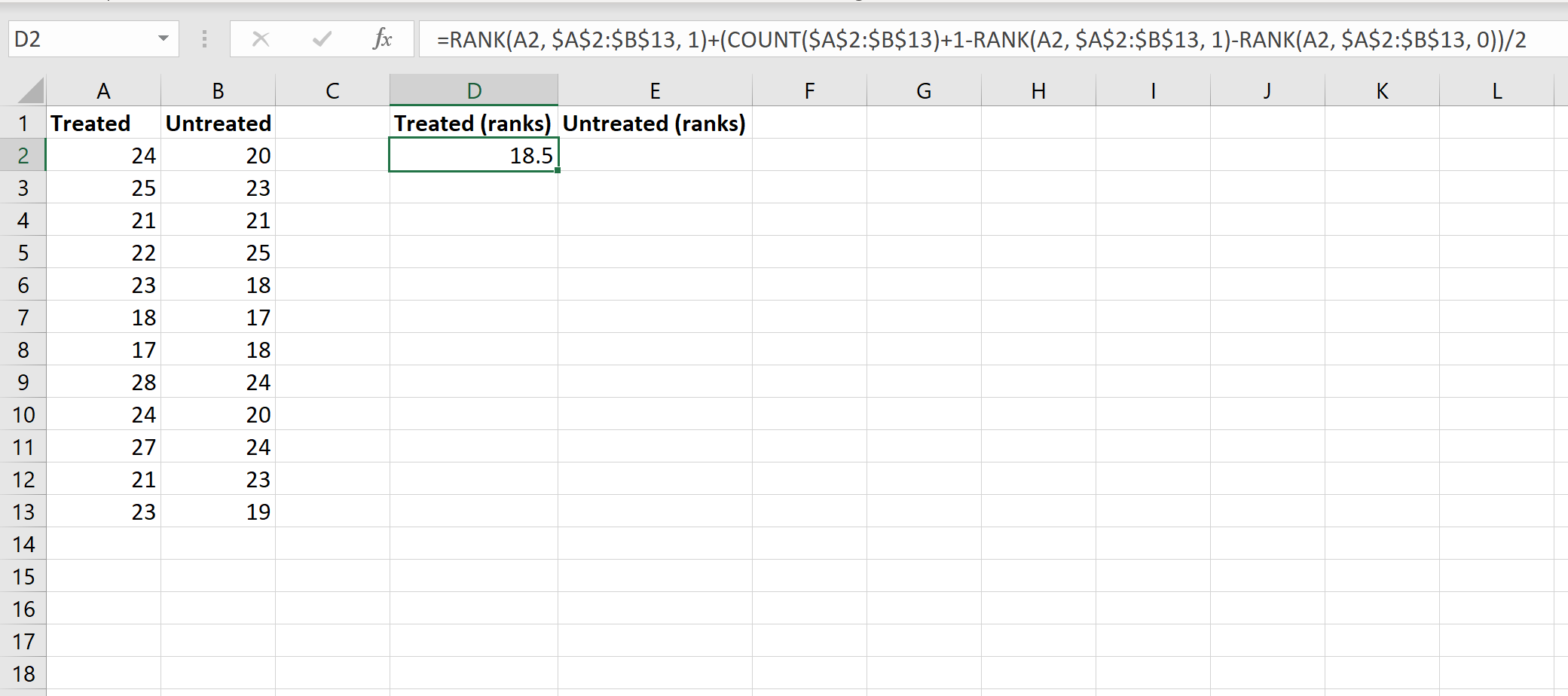
Obwohl diese Formel recht kompliziert ist, müssen Sie sie nur einmal eingeben. Dann können Sie die Formel einfach in alle anderen Zellen ziehen, um die Zeilen zu füllen:

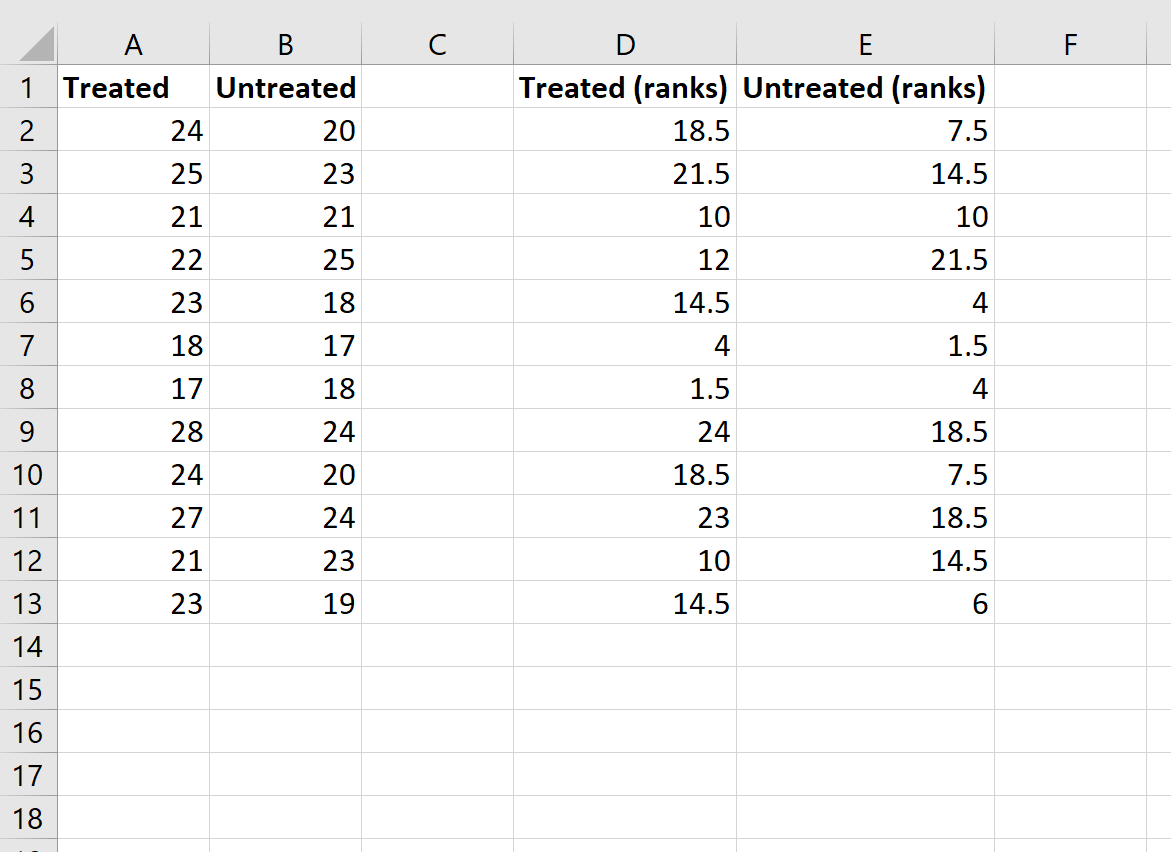
Schritt 3: Berechnen Sie die für die Teststatistik benötigten Werte.

Als Nächstes verwenden wir die folgenden Formeln, um die Summe der Ränge für jede Gruppe, die Stichprobengröße für jede Gruppe, die U-Test-Statistik für jede Gruppe und die gesamte U-Test-Statistik zu berechnen:

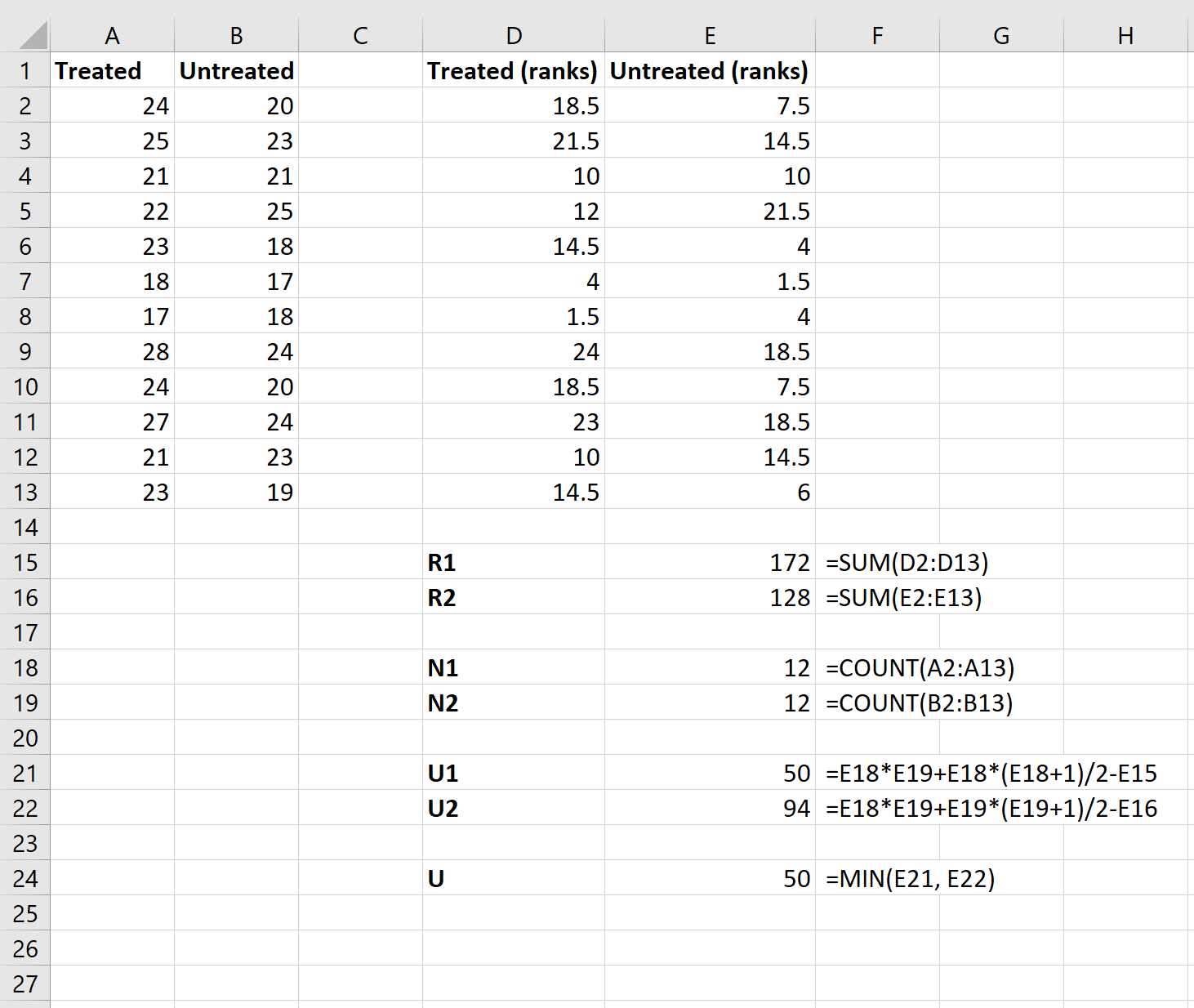
Schritt 4: Berechnen Sie die Z-Test-Statistik und den entsprechenden p-Wert.

Abschließend verwenden wir die folgenden Formeln, um die Z-Test-Statistik und den entsprechenden p-Wert zu berechnen, um zu bestimmen, ob wir die Nullhypothese ablehnen sollten oder nicht:

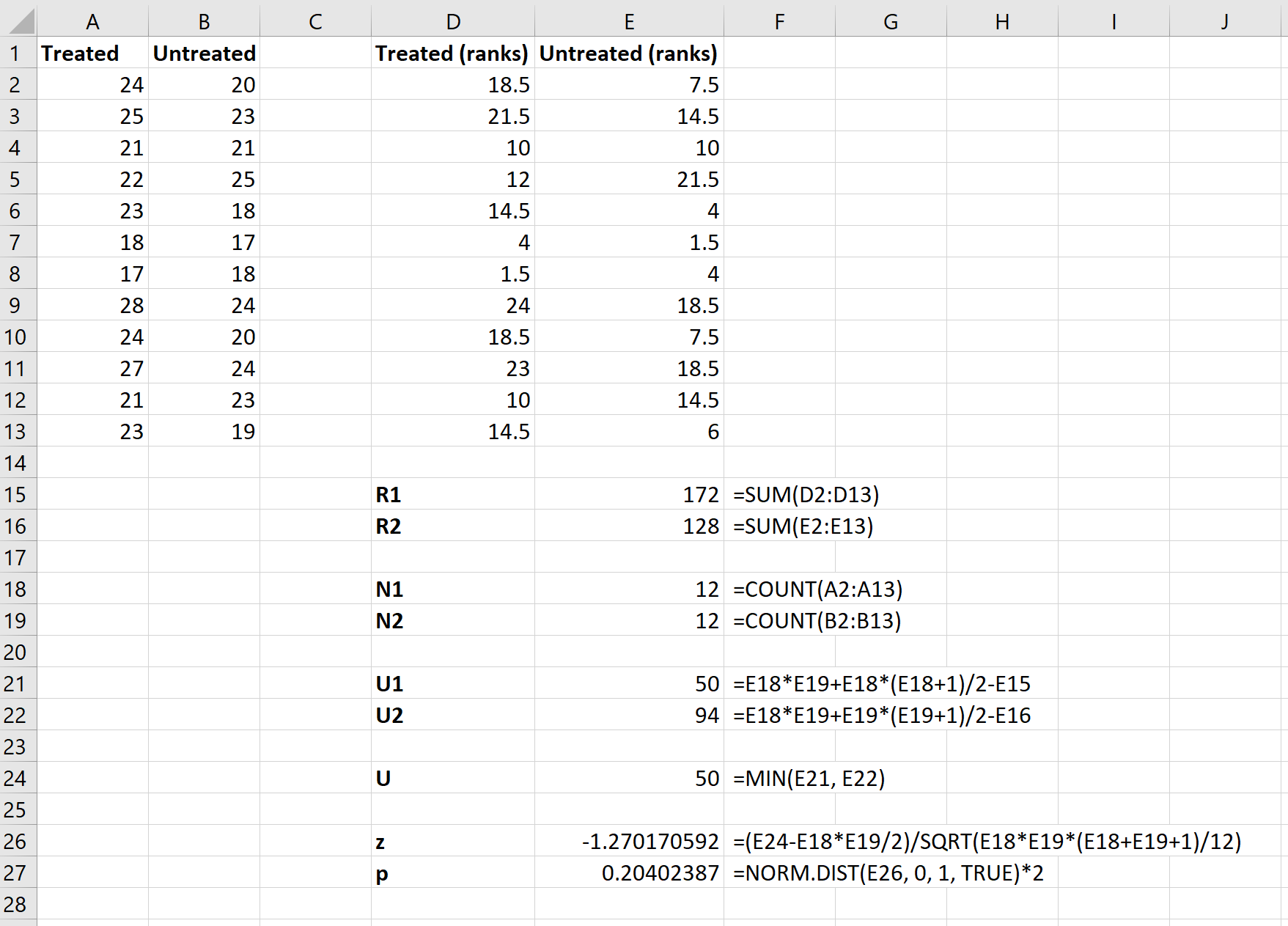
Die Nullhypothese des Tests besagt, dass beide Gruppen die gleichen durchschnittlichen mpg haben. Da der Test-p-Wert ( 0,20402387 ) nicht unter unserem Signifikanzniveau von 0,05 liegt, können wir die Nullhypothese nicht ablehnen.

Wir haben nicht genügend Beweise, um sagen zu können, dass der tatsächliche durchschnittliche MPG-Wert zwischen den beiden Gruppen unterschiedlich ist.