So berechnen sie die spearman-rangkorrelation in excel

In der Statistik bezeichnet Korrelation die Stärke und Richtung einer Beziehung zwischen zwei Variablen. Der Wert eines Korrelationskoeffizienten kann zwischen -1 und 1 liegen, mit folgenden Interpretationen:

• -1: eine perfekte negative Beziehung zwischen zwei Variablen
• 0: keine Beziehung zwischen zwei Variablen
• 1: eine perfekte positive Beziehung zwischen zwei Variablen

Eine besondere Art der Korrelation ist die Spearman-Rangkorrelation , mit der die Korrelation zwischen zwei Rangvariablen gemessen wird. (z. B. die Rangfolge der Mathematikprüfungsergebnisse eines Schülers im Verhältnis zur Rangfolge seiner naturwissenschaftlichen Prüfungsergebnisse in einer Klasse).

In diesem Tutorial wird erläutert, wie Sie die Spearman-Rangkorrelation zwischen zwei Variablen in Excel berechnen.

Beispiel: Spearman-Rangkorrelation in Excel

Führen Sie die folgenden Schritte aus, um die Spearman-Rangkorrelation zwischen der Punktzahl in der Mathematikprüfung und der Punktzahl in der naturwissenschaftlichen Prüfung von 10 Schülern in einer bestimmten Klasse zu berechnen.

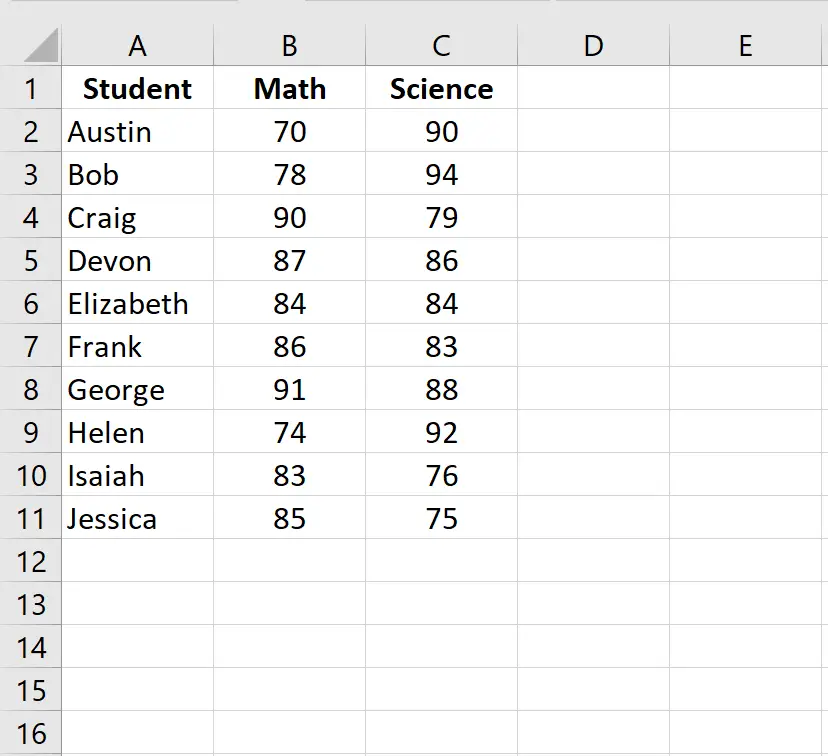
Schritt 1: Geben Sie die Daten ein.

Geben Sie die Prüfungsergebnisse jedes Schülers in zwei separaten Spalten ein:

Schritt 2: Berechnen Sie die Rangfolge für jedes Prüfungsergebnis.

Als nächstes berechnen wir die Rangfolge für jedes Prüfungsergebnis. Verwenden Sie die folgenden Formeln in den Zellen D2 und E2, um die Ränge in Mathematik und Naturwissenschaften für den ersten Schüler, Austin, zu berechnen:

Zelle D2: =RANK.AVG(B2, $B$2:$B$11, 0)

Zelle E2: =RANK.AVG(C2, $C$2:$C$11, 0)

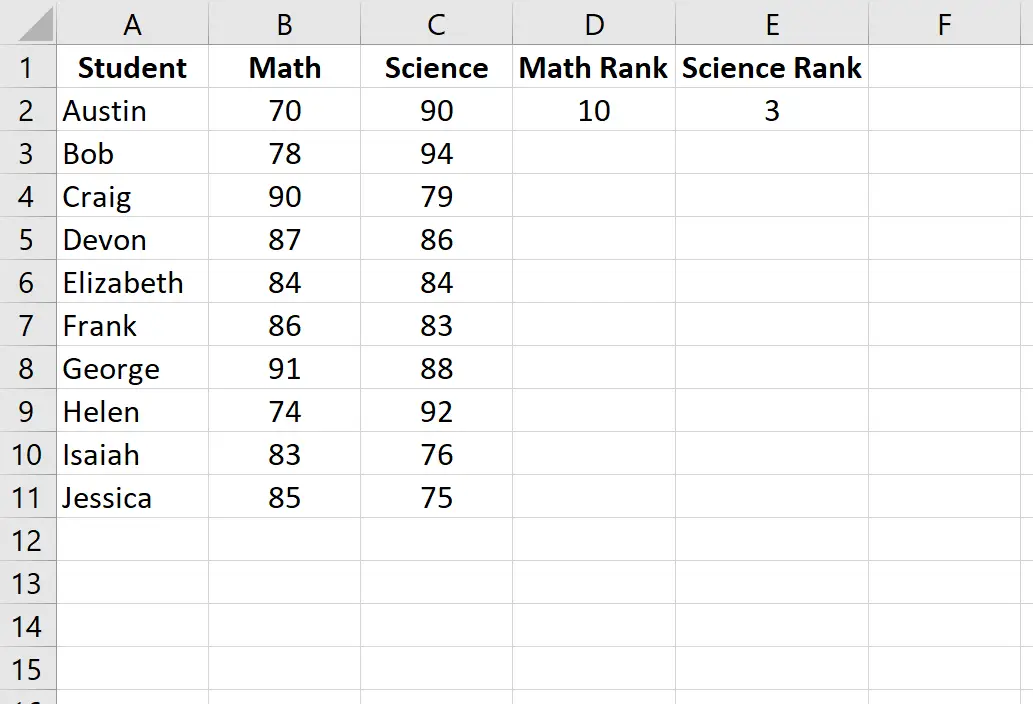
Markieren Sie als Nächstes die verbleibenden auszufüllenden Zellen:

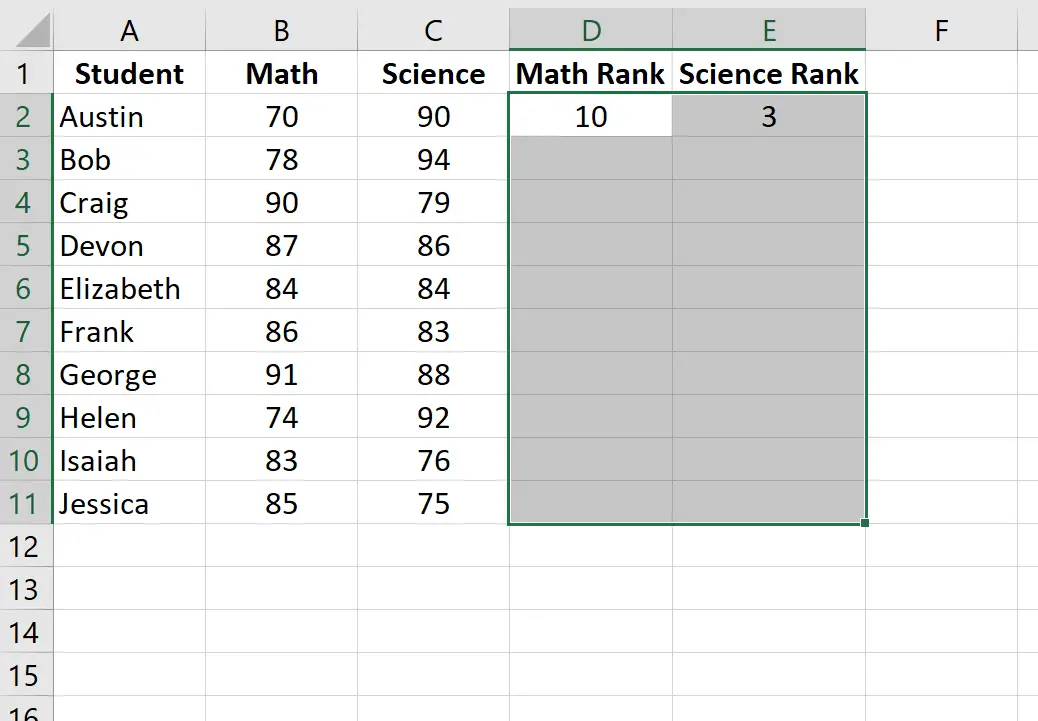
Klicken Sie dann auf Strg+D, um die Rangliste jedes Schülers einzugeben:

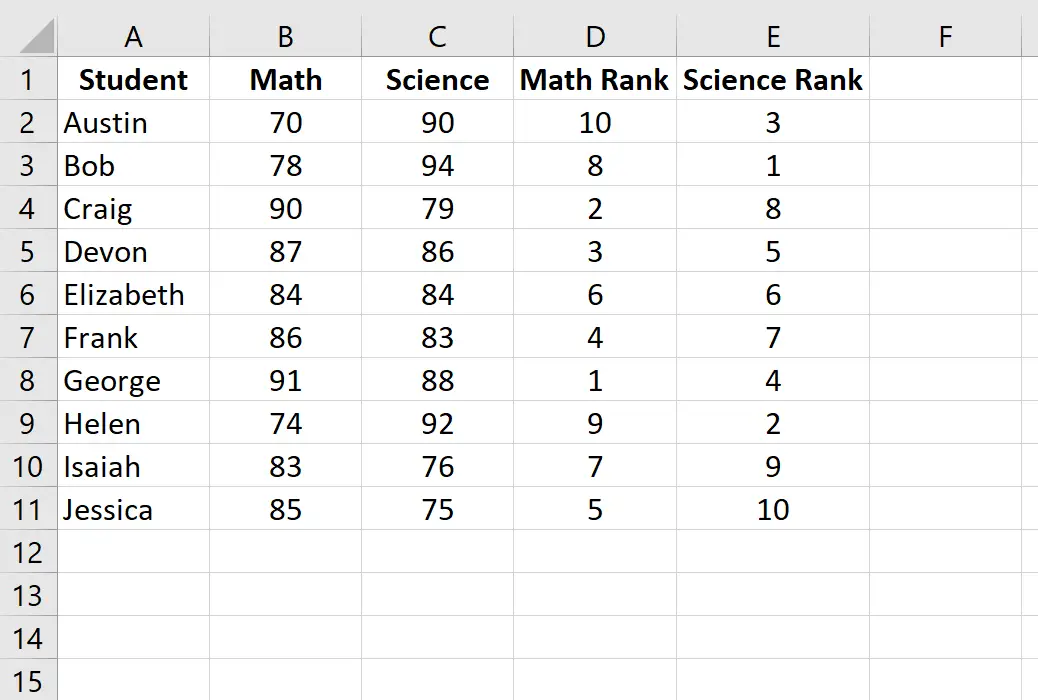
Schritt 3: Berechnen Sie den Spearman-Rangkorrelationskoeffizienten.

Abschließend berechnen wir den Spearman-Rangkorrelationskoeffizienten zwischen den Mathematik- und Naturwissenschaftsergebnissen mithilfe der Funktion CORREL() :

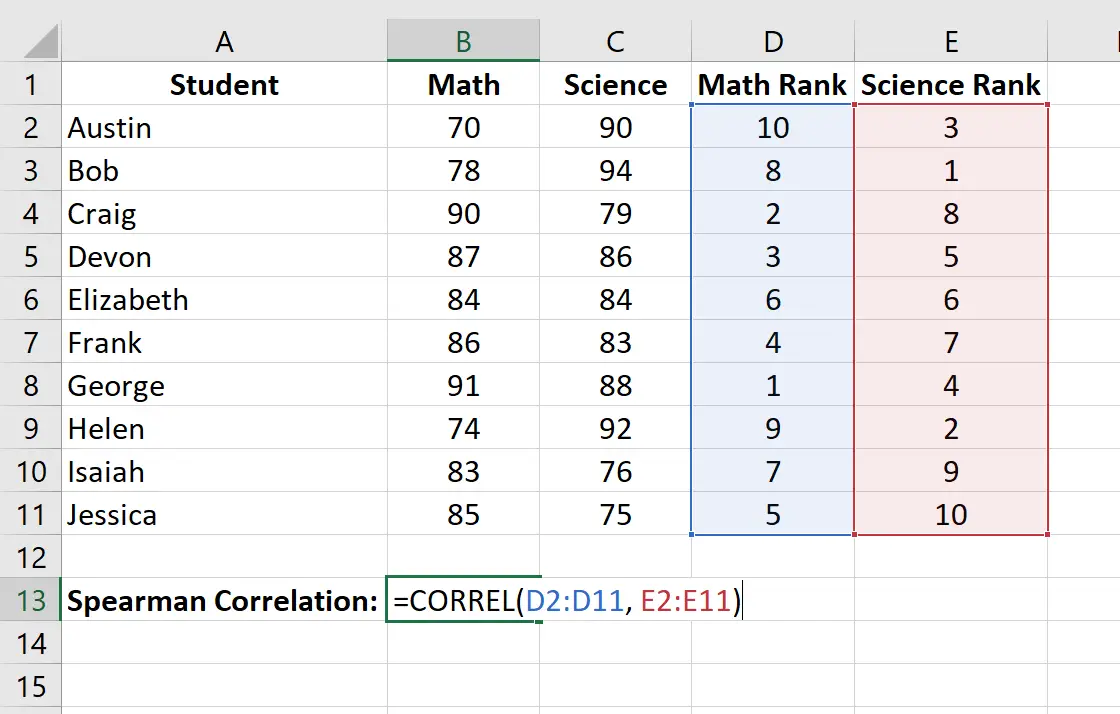
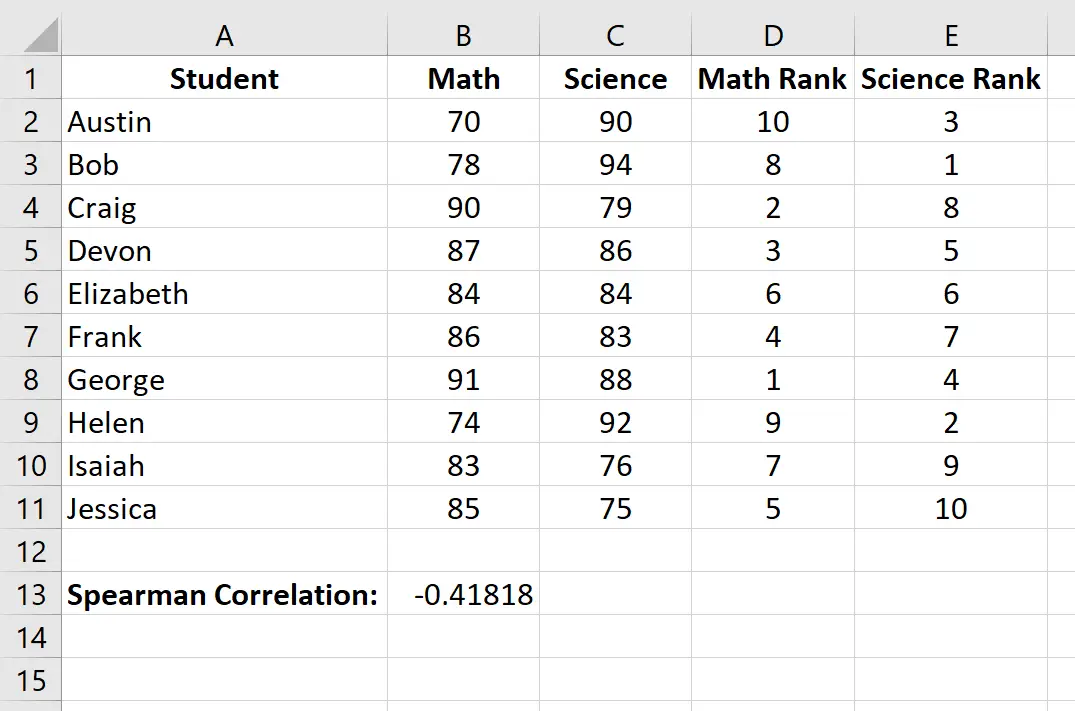
Die Spearman-Rangkorrelation beträgt -0,41818 .

Schritt 4 (optional): Bestimmen Sie, ob die Spearman-Rangkorrelation statistisch signifikant ist.

Im vorherigen Schritt haben wir festgestellt, dass die Spearman-Rangkorrelation zwischen den Prüfungsergebnissen in Mathematik und Naturwissenschaften -0,41818 betrug, was auf eine negative Korrelation zwischen den beiden Variablen hinweist.

Um jedoch festzustellen, ob diese Korrelation statistisch signifikant ist, müssten wir auf eine Spearman-Rangkorrelationstabelle kritischer Werte zurückgreifen, die die kritischen Werte zeigt, die mit verschiedenen Stichprobengrößen (n) und Signifikanzniveaus (α) verbunden sind.

Wenn der absolute Wert unseres Korrelationskoeffizienten größer ist als der kritische Wert in der Tabelle, dann ist die Korrelation zwischen den beiden Variablen statistisch signifikant.

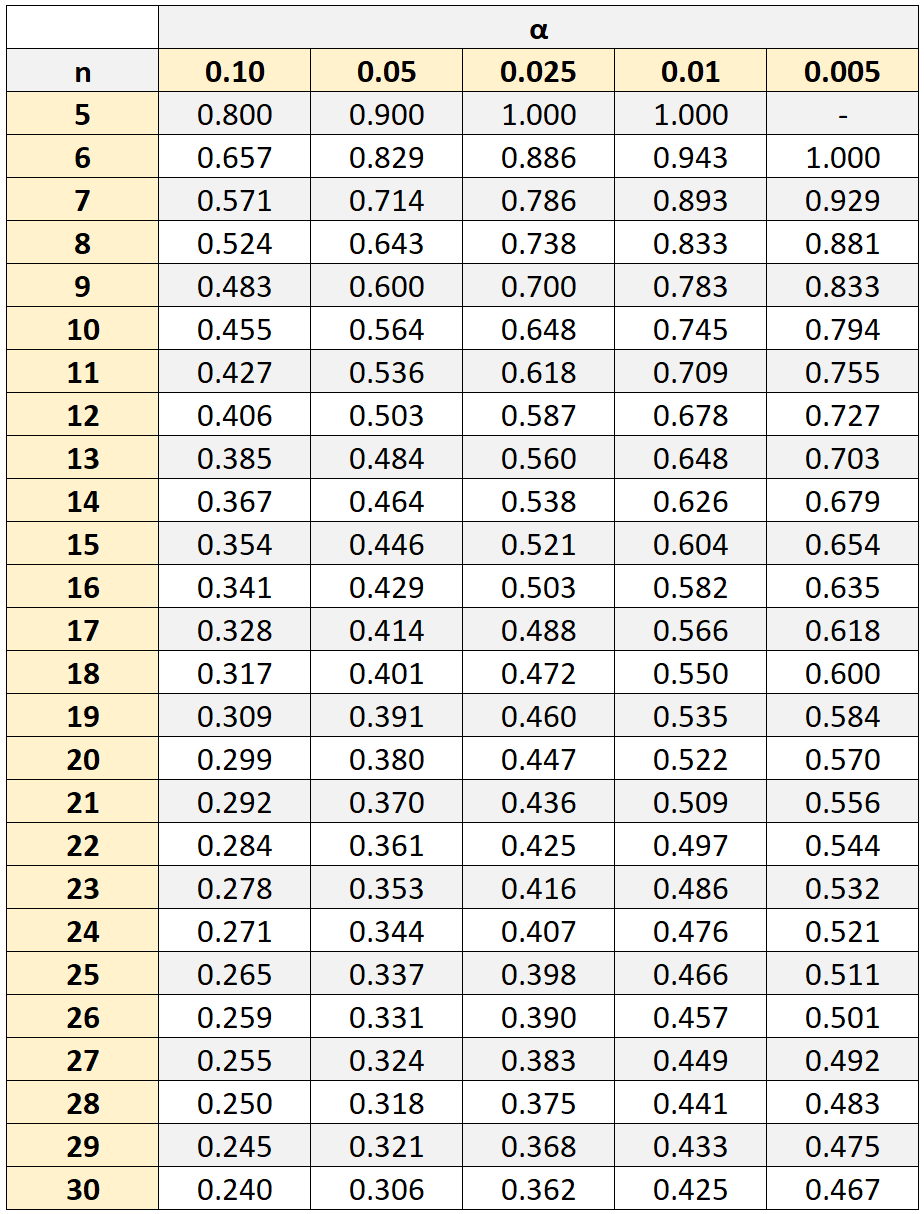
In unserem Beispiel betrug unsere Stichprobengröße n = 10 Studierende. Bei einem Signifikanzniveau von 0,05 ermitteln wir, dass der kritische Wert 0,564 beträgt.

Da der absolute Wert des von uns berechneten Spearman-Rangkorrelationskoeffizienten ( 0,41818 ) nicht größer als dieser kritische Wert ist, bedeutet dies, dass die Korrelation zwischen Mathematik- und Naturwissenschaftsergebnissen statistisch nicht signifikant ist.