Varianz

Von Dr. Benjamin Anderson August 5, 2023 Statistiken Keine Kommentare

In diesem Artikel erklären wir, was Varianz, auch Varianz genannt, ist und wie sie berechnet wird. Sie finden die Varianzformel, ein konkretes Beispiel zur Varianzberechnung und können darüber hinaus die Varianz eines beliebigen Datensatzes mit einem Online-Rechner berechnen.

Wir zeigen Ihnen auch, wie Sie die Varianz gruppierter Daten ermitteln, da dies auf andere Weise geschieht. Abschließend zeigen wir Ihnen den Unterschied zwischen Populationsvarianz und Stichprobenvarianz, den Unterschied zwischen Varianz und Standardabweichung und die Eigenschaften dieses statistischen Maßes.

Was ist Varianz?

In der Statistik ist Varianz ein Maß für die Streuung, das die Variabilität einer Zufallsvariablen angibt. Die Varianz entspricht der Summe der Quadrate der Residuen dividiert durch die Gesamtzahl der Beobachtungen.

Beachten Sie, dass unter dem Residuum die Differenz zwischen dem Wert eines statistischen Datenpunkts und dem Mittelwert des Datensatzes verstanden wird.

In der Wahrscheinlichkeitstheorie ist das Symbol für Varianz der griechische Buchstabe Sigma im Quadrat (σ ² ). Normalerweise wird es jedoch auch als Var(X) dargestellt, wobei X die Zufallsvariable ist, aus der die Varianz berechnet wird.

Im Allgemeinen ist die Interpretation des Varianzwerts einer Zufallsvariablen einfach. Je größer der Varianzwert, desto stärker gestreut sind die Daten. Und umgekehrt gilt: Je kleiner der Varianzwert, desto geringer ist die Streuung in der Datenreihe. Allerdings muss man bei der Interpretation der Varianz auf Ausreißer achten, da diese den Varianzwert verzerren können.

Neben der Varianz werden neben der Streuung auch die Spanne, die Standardabweichung, die mittlere Abweichung und der Variationskoeffizient berücksichtigt.

So berechnen Sie die Lücke

Um die Varianz zu berechnen, müssen folgende Schritte durchgeführt werden:

Ermitteln Sie das arithmetische Mittel des Datensatzes.
Berechnen Sie die Residuen, definiert als Differenz zwischen den Werten und dem Mittelwert des Datensatzes.
Quadrieren Sie jeden Rest.
Addieren Sie alle im vorherigen Schritt berechneten Ergebnisse.
Teilen Sie durch die Gesamtzahl der Daten. Das erhaltene Ergebnis ist die Varianz der Datenreihe.

Zusammenfassend lautet die Formel zur Berechnung der Varianz eines Datensatzes:

Gold:

$X$

ist die Zufallsvariable, für die Sie die Varianz berechnen möchten.
$x_i$

ist der Datenwert

$i$

.
$n$

ist die Gesamtzahl der Beobachtungen.
$\overline{X}$

ist der Mittelwert der Zufallsvariablen

$X$

.

👉 Mit dem Rechner unten können Sie die Varianz eines beliebigen Datensatzes berechnen.

Um die Varianz aus einer Datenreihe zu extrahieren, ist es daher wichtig, dass Sie wissen, wie das arithmetische Mittel berechnet wird. Wenn Sie nicht wissen, wie das geht, können Sie es im oben verlinkten Artikel nachlesen.

Beispiel einer Abweichung

Nachdem wir nun die Definition der Varianz kennen, lösen wir eine Übung Schritt für Schritt, damit Sie sehen können, wie die Varianz einer Datenreihe ermittelt wird.

Von einem multinationalen Unternehmen ist das wirtschaftliche Ergebnis bekannt, das es in den letzten fünf Jahren erzielt hat. In den meisten Fällen erzielte es Gewinne, in einem Jahr verzeichnete es jedoch erhebliche Verluste: 11,5, 2, -9, 7 Millionen Euro. Berechnen Sie die Varianz dieses Datensatzes.

Wie wir in der obigen Erklärung gesehen haben, müssen wir zum Ermitteln der Varianz einer Datenreihe zunächst ihr arithmetisches Mittel berechnen:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

Und sobald wir den Durchschnittswert der Daten kennen, können wir die Varianzformel verwenden:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

Wir setzen die in der Übungserklärung bereitgestellten Daten in die Formel ein:

$Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}$

Abschließend müssen nur noch die Operationen zur Berechnung der Varianz gelöst werden:

$\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}$

Beachten Sie, dass es sich bei den Varianzeinheiten um die gleichen Einheiten der statistischen Daten handelt, jedoch quadriert. Aus diesem Grund beträgt die Varianz dieser Datengruppe 45,76 Millionen Euro ² .

Lückenrechner

Geben Sie einen statistischen Datensatz in den folgenden Rechner ein, um dessen Varianz zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Varianz für gruppierte Daten

Um die Varianz von in Intervallen gruppierten Daten zu berechnen , müssen die folgenden Schritte befolgt werden:

Ermitteln Sie den Mittelwert der gruppierten Daten.
Berechnen Sie die Residuen der gruppierten Daten.
Quadrieren Sie jeden Rest.
Multiplizieren Sie jedes vorherige Ergebnis mit der Häufigkeit seines Intervalls.
Addieren Sie die Summe aller im vorherigen Schritt erhaltenen Werte.
Teilen Sie durch die Gesamtzahl der Beobachtungen. Die resultierende Zahl ist die Varianz der gruppierten Daten.

Mit anderen Worten lautet die Formel zur Berechnung der Varianz von in Intervallen gruppierten Daten wie folgt:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}$

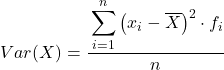
Obwohl normalerweise die obige Formel verwendet wird, kann auch der folgende algebraische Ausdruck verwendet werden, da er äquivalent ist:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2$

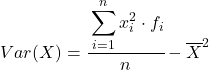
Als Beispiel finden wir die Varianz der folgenden gruppierten Datenreihen:

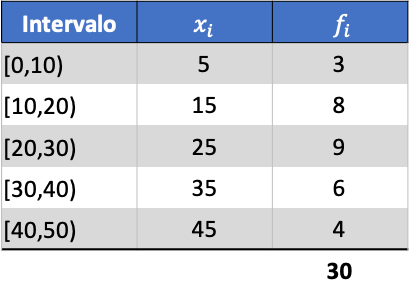
Zuerst müssen wir den Durchschnitt der gruppierten Daten ermitteln. Dazu fügen wir in der Häufigkeitstabelle eine Spalte mit dem Produkt aus Klassennote und Häufigkeit ein:

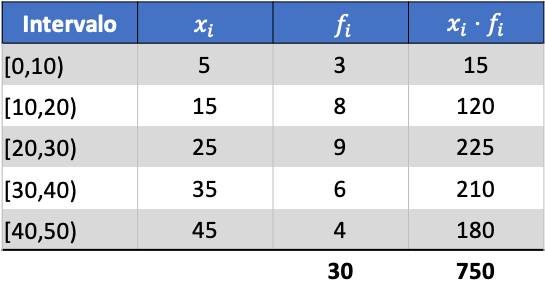
Wir berechnen nun den Durchschnitt der gruppierten Daten, indem wir die Summe der hinzugefügten Spalte durch die Gesamtzahl der Daten dividieren:

$\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25$

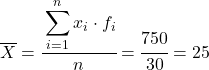
Und aus dem Durchschnitt der berechneten Daten können wir die folgenden drei Spalten hinzufügen:

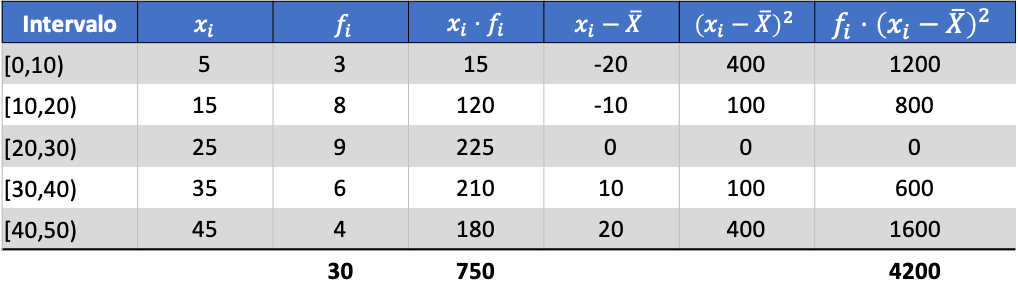
Die Varianz des gepoolten Datensatzes ist also die Summe der letzten Spalte dividiert durch die Gesamtzahl der beobachteten Daten:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140$

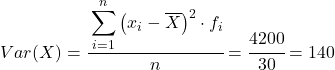
Varianz und Standardabweichung

Varianz und Standardabweichung (oder Standardabweichung) sind zwei Streuungsmaße und geben daher beide den Grad der Streuung des Datensatzes an. Der Unterschied zwischen Varianz und Standardabweichung besteht jedoch darin, dass die Varianz im Allgemeinen größere Werte hat, da sie das Quadrat der Standardabweichung ist.

Die Standardabweichung wird im Allgemeinen durch den griechischen Buchstaben Sigma (σ) dargestellt, und aus diesem Grund wird die Varianz durch den Buchstaben Sigma im Quadrat (σ ² ) dargestellt, da es sich um die mathematische Beziehung handelt, die zwischen diesen beiden Streuungsmetriken besteht.

$Var(X)=\sigma^2$

Sobald Sie also den Varianzwert eines Datensatzes berechnet haben, können Sie den Standardabweichungswert desselben Satzes leicht ermitteln, indem Sie einfach die Quadratwurzel der Varianz ziehen.

$\sigma=\sqrt{\sigma^2}$

Populationsvarianz und Stichprobenvarianz

Logischerweise bezieht sich die Populationsvarianz auf die Berechnung der Varianz einer statistischen Grundgesamtheit und stattdessen wird die Stichprobenvarianz auf die Berechnung der Varianz einer Stichprobe angewendet. Dabei handelt es sich jedoch um zwei unterschiedliche Konzepte, da sich die Populationsvarianzformel von der Stichprobenvarianzformel unterscheidet.

Normalerweise müssen wir in Varianzübungen, sofern sie uns nichts anderes sagen, zur Ermittlung der Varianz des bereitgestellten Datensatzes die Grundgesamtheitsvarianzformel verwenden, die wir am Anfang des Artikels erklärt haben:

$\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

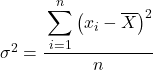
Aber vielleicht werden Sie bei manchen Problemen aufgefordert, statistische Daten als Stichprobe zu behandeln. In diesem Fall müssen wir die Stichprobenvarianzformel verwenden:

$s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

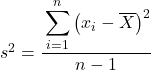
Beachten Sie, dass zur Angabe, dass eine Populationsvarianz berechnet wird, diese durch den griechischen Buchstaben σ gekennzeichnet wird, bei der Berechnung einer Stichprobenvarianz jedoch der Buchstabe s verwendet wird.

Wie Sie sehen, besteht der einzige Unterschied zwischen den beiden Formeln darin, dass wir die Varianz einer Stichprobe durch die Gesamtzahl der Beobachtungen minus 1 dividieren müssen. Wenn es beispielsweise insgesamt 30 Datenelemente gibt, dividieren wir durch 29 Die Berechnung des Zählers erfolgt jedoch genauso.

Varianzeigenschaften

Die Varianz hat folgende Eigenschaften:

Die Varianz jeder Zufallsvariablen ist immer größer oder gleich Null. Wenn die Varianz Null ist, bedeutet dies ebenfalls, dass alle statistischen Daten gleich sind.

$Var(x)\ge 0$

Offensichtlich ist die Varianz eines einzelnen Werts Null.

$Var(a)=0\qquad a\in \mathbb{R}$

Die Varianz des Produkts eines Skalars mit einer Variablen entspricht dem Quadrat des Skalars multipliziert mit der Varianz der Variablen.

$Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}$

Die Varianz der Summe zweier abhängiger Variablen entspricht der Summe der Varianz jeder einzelnen Variablen plus dem Doppelten der Kovarianz zwischen den beiden Variablen.

$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$

Wenn also die beiden Variablen unabhängig sind, reicht es zur Bestimmung der Varianz ihrer Summe aus, ihre Varianzen zu addieren:

$Var(X+Y)=Var(X)+Var(Y)$

Die Abweichung kann auch mit dem mathematischen Erwartungswert nach folgender Formel definiert werden:

$Var(X)=E\bigl[(X-\overline{X})^2\bigr]$

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen