So normalisieren sie daten in excel
Eine Reihe von Datenwerten zu „normalisieren“ bedeutet, die Werte so zu skalieren, dass der Mittelwert aller Werte 0 und die Standardabweichung 1 beträgt.
In diesem Tutorial wird erläutert, wie Sie Daten in Excel normalisieren.
Beispiel: So normalisieren Sie Daten in Excel
Angenommen, wir haben den folgenden Datensatz in Excel:
Führen Sie die folgenden Schritte aus, um diesen Satz von Datenwerten zu normalisieren.
Schritt 1: Ermitteln Sie den Mittelwert.
Zuerst verwenden wir die Funktion =AVERAGE(Wertebereich), um den Durchschnitt des Datensatzes zu ermitteln.
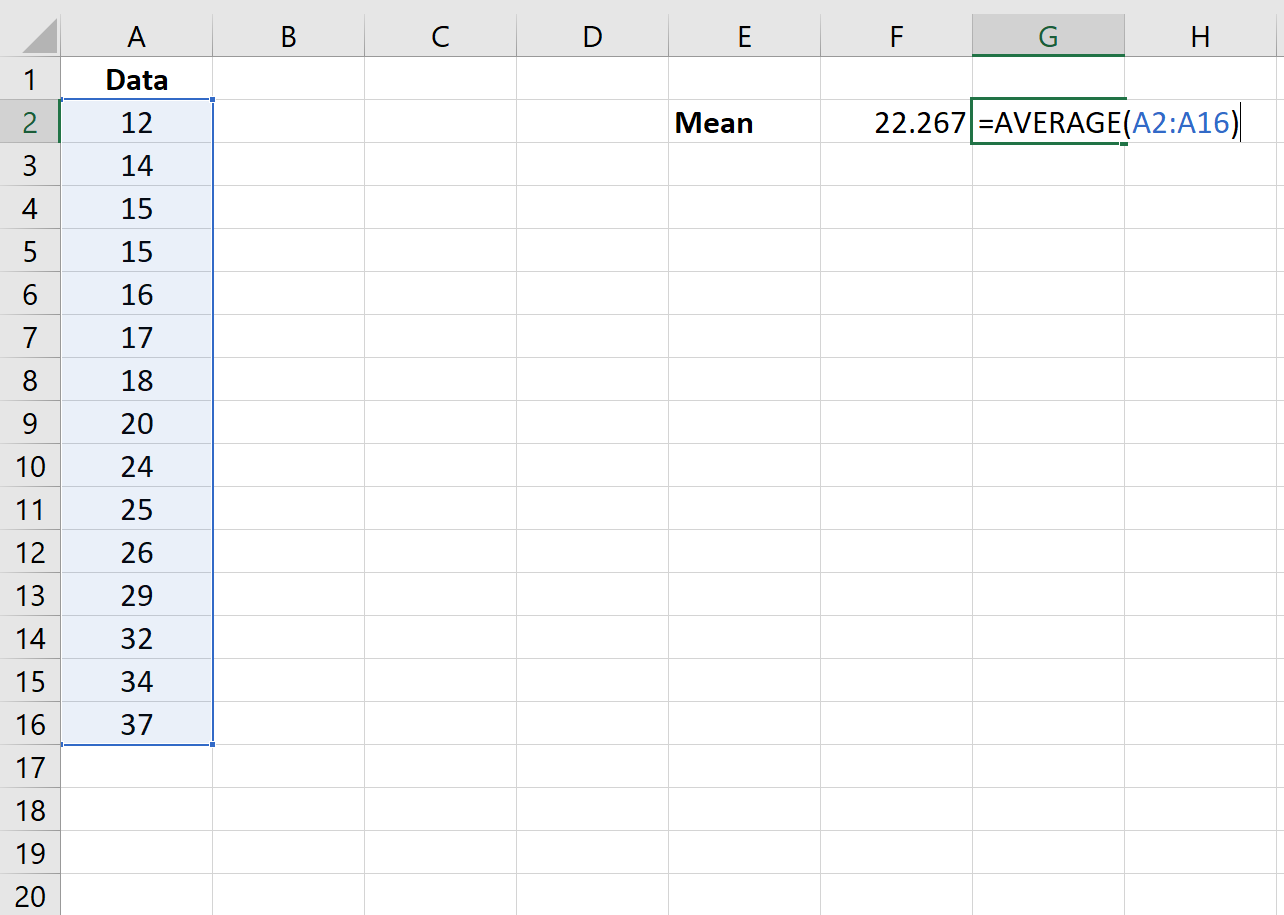
Schritt 2: Ermitteln Sie die Standardabweichung.
Als nächstes verwenden wir die Funktion =STDEV (Wertebereich), um die Standardabweichung des Datensatzes zu ermitteln.
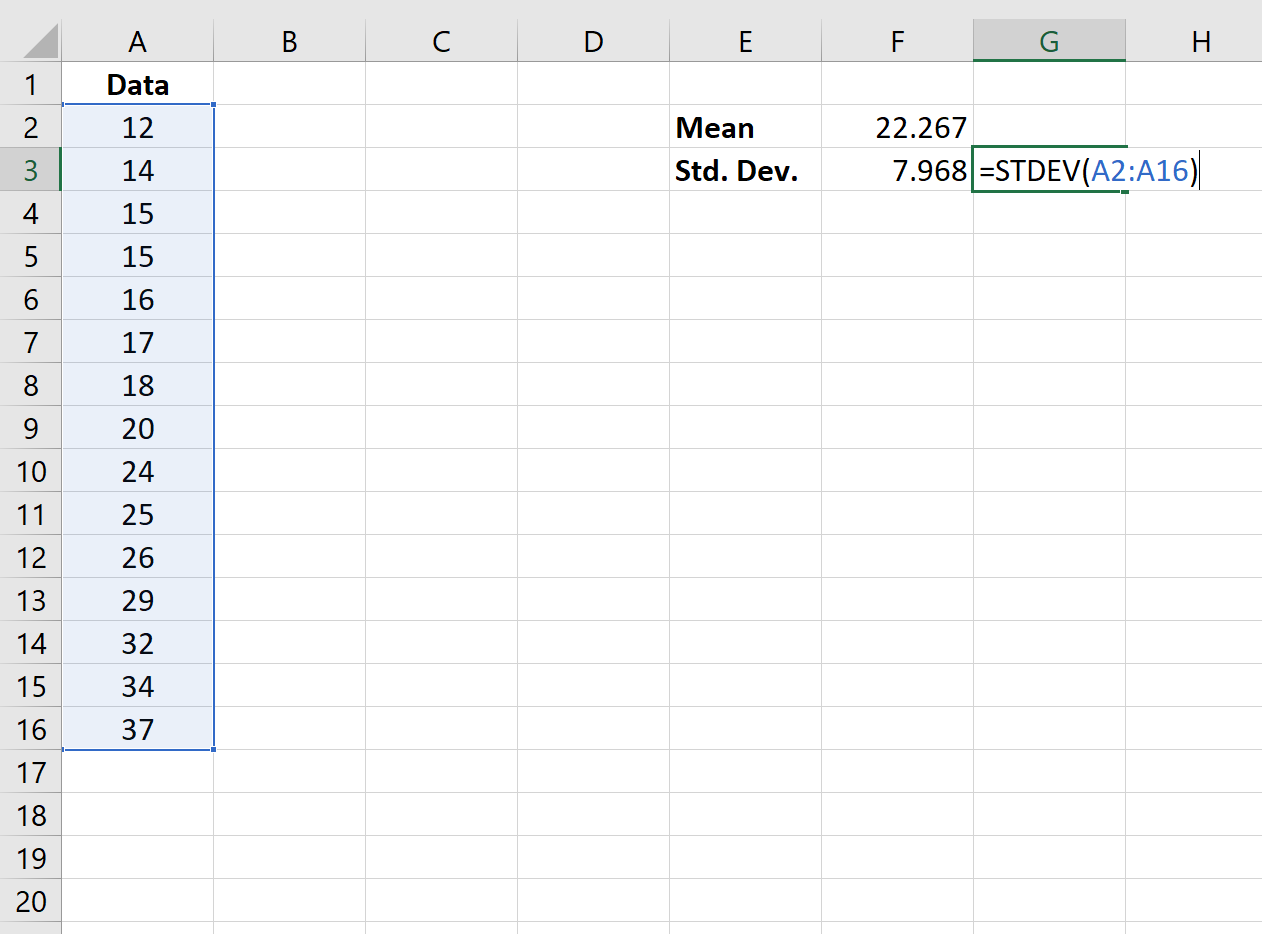
Schritt 3: Normalisieren Sie die Werte.
Abschließend verwenden wir die Funktion STANDARDIZE(x, Mean, standard_dev) , um jeden Wert im Datensatz zu normalisieren.
NOTIZ:
Die Funktion STANDARDIZE verwendet die folgende Formel, um einen bestimmten Datenwert zu normalisieren:
Normalisierter Wert = (x – x ) / s
Gold:
- x = Datenwert
- x = Mittelwert des Datensatzes
- s = Standardabweichung des Datensatzes
Das folgende Bild zeigt die Formel zur Normalisierung des ersten Werts im Datensatz:
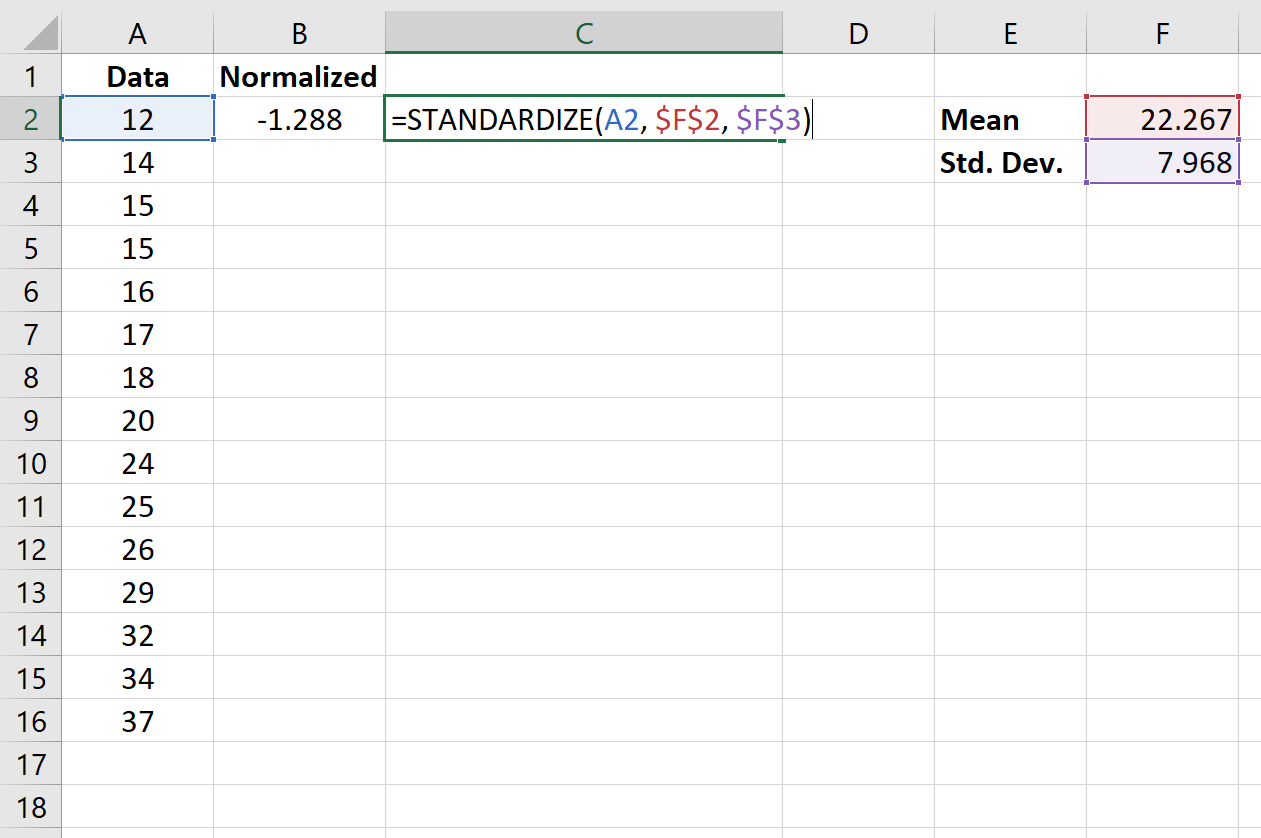
Sobald wir den ersten Wert in Zelle B2 normalisiert haben, können wir mit der Maus über die rechte untere Ecke von Zelle B2 fahren, bis ein kleines + erscheint. Doppelklicken Sie auf das + , um die Formel in die verbleibenden Zellen zu kopieren:
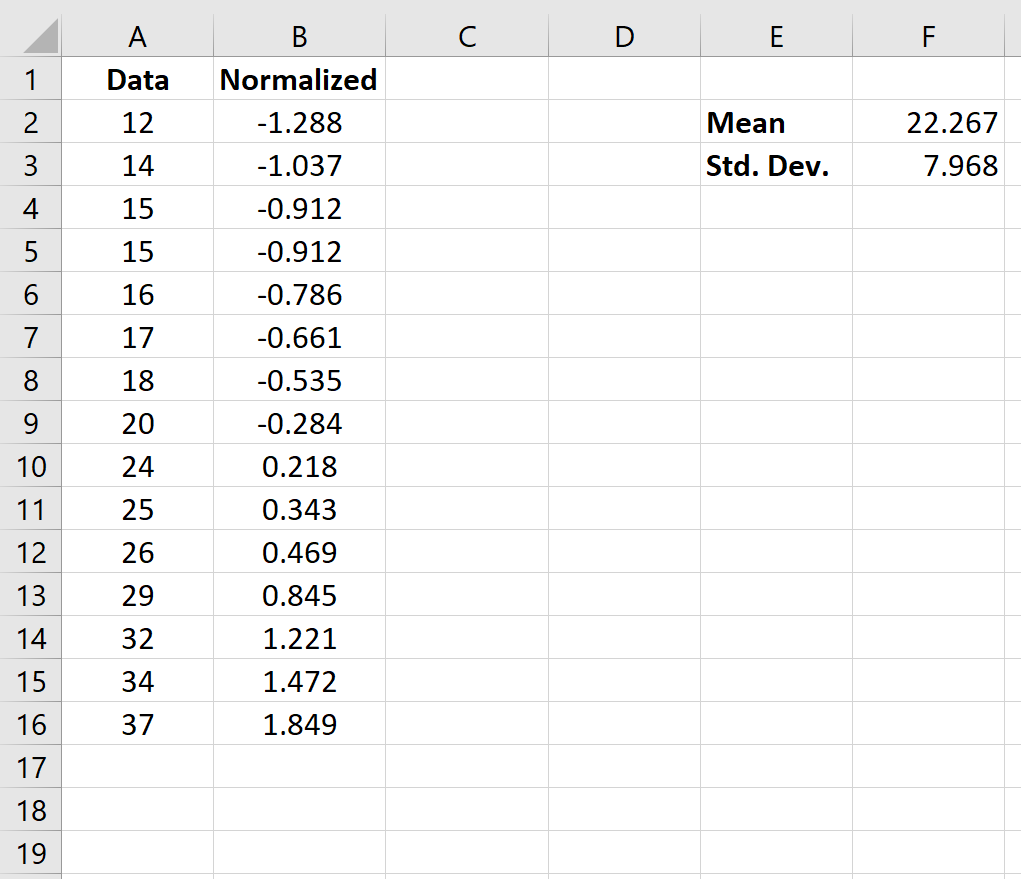
Jetzt wird jeder Wert im Datensatz normalisiert.
So interpretieren Sie normalisierte Daten
Die Formel, die wir zur Normalisierung eines bestimmten Datenwerts x verwendet haben, war:
Normalisierter Wert = (x – x ) / s
Gold:
- x = Datenwert
- x = Mittelwert des Datensatzes
- s = Standardabweichung des Datensatzes
Wenn ein bestimmter Datenpunkt einen normalisierten Wert größer als 0 aufweist, weist dies darauf hin, dass der Datenpunkt über dem Durchschnitt liegt. Umgekehrt bedeutet ein normalisierter Wert kleiner als 0, dass der Datenpunkt unter dem Durchschnitt liegt.
Insbesondere sagt uns der normalisierte Wert, wie viele Standardabweichungen der ursprüngliche Datenpunkt vom Mittelwert hat. Betrachten Sie beispielsweise den Datenpunkt „12“ in unserem Originaldatensatz:
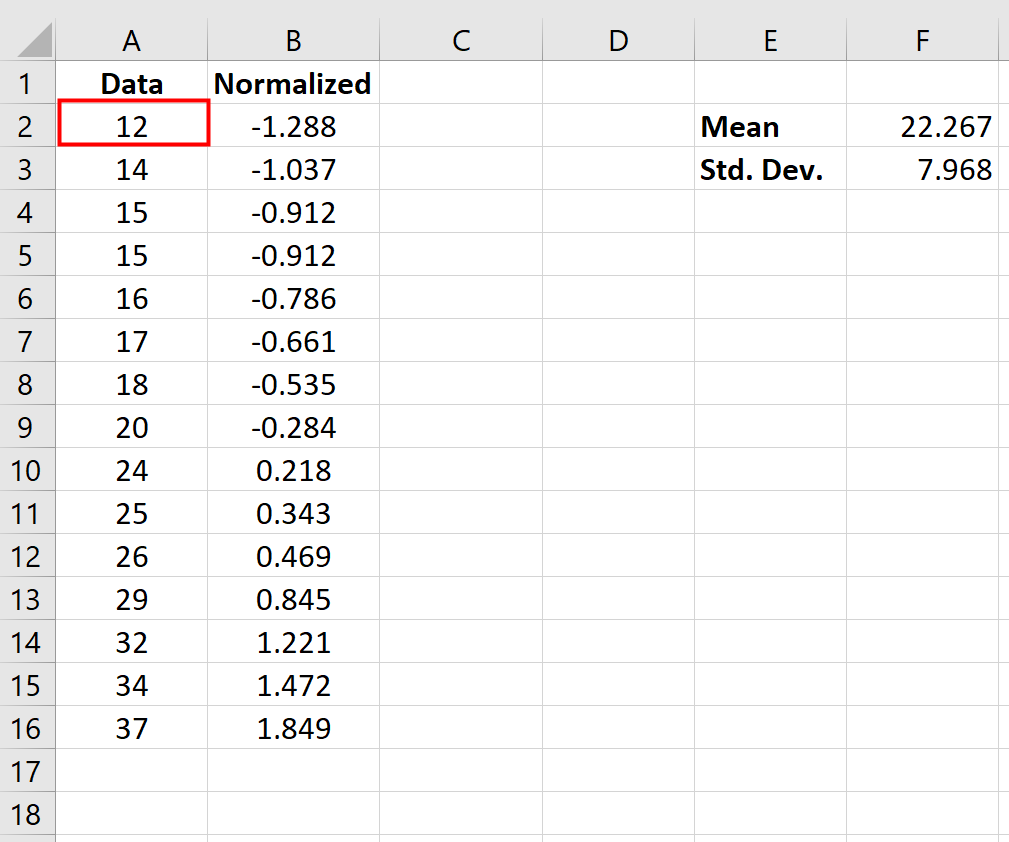
Der normalisierte Wert für „12“ betrug -1,288 und wurde wie folgt berechnet:
Normalisierter Wert = (x – x ) / s = (12 – 22,267) / 7,968 = -1,288
Dies sagt uns, dass der Wert „12“ 1,288 Standardabweichungen niedriger ist als der Mittelwert des Originaldatensatzes.
Jeder der normalisierten Werte im Datensatz kann uns helfen zu verstehen, wie nahe oder weit ein bestimmter Datenwert vom Mittelwert entfernt ist. Ein kleiner normalisierter Wert zeigt an, dass ein Wert nahe am Mittelwert liegt, während ein großer normalisierter Wert angibt, dass ein Wert weit vom Mittelwert entfernt ist.