Was sind zufallsvariablen?

Eine Zufallsvariable , allgemein mit X bezeichnet, ist eine Variable, deren mögliche Werte das Ergebnis eines Zufallsprozesses sind.

Es gibt zwei Arten von Zufallsvariablen: diskrete und kontinuierliche .

Diskrete Zufallsvariablen

Eine diskrete Zufallsvariable ist eine Variable, die nur eine abzählbare Anzahl unterschiedlicher Werte wie 0, 1, 2, 3, 4, 5…100, 1 Million usw. annehmen kann. Hier sind einige Beispiele für diskrete Zufallsvariablen:

• Die Häufigkeit, mit der eine Münze „Zahl“ erhält, nachdem sie 20 Mal geworfen wurde.
• Die Häufigkeit, mit der ein Würfel auf der Zahl 4 landet, nachdem er 100 Mal gewürfelt wurde.
• Die Anzahl defekter Widgets in einer Schachtel mit 50 Widgets.

Eine Wahrscheinlichkeitsverteilung für eine diskrete Zufallsvariable gibt uns die Wahrscheinlichkeit an, mit der die Zufallsvariable bestimmte Werte annimmt.

Angenommen, wir würfeln einmal mit einem fairen Würfel. Wenn wir X die Wahrscheinlichkeit bezeichnen, dass der Würfel auf eine bestimmte Zahl fällt, dann lässt sich die Wahrscheinlichkeitsverteilung wie folgt schreiben:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Notiz:

Damit eine Wahrscheinlichkeitsverteilung gültig ist, muss sie die folgenden zwei Kriterien erfüllen:

1. Die Wahrscheinlichkeit jedes Ergebnisses muss zwischen 0 und 1 liegen.

2. Die Summe aller Wahrscheinlichkeiten muss 1 ergeben.

Beachten Sie, dass die Wahrscheinlichkeitsverteilung für den Würfelwurf diese beiden Kriterien erfüllt:

1. Die Wahrscheinlichkeit jedes Ergebnisses liegt zwischen 0 und 1.

2. Die Summe aller Wahrscheinlichkeiten ergibt 1.

Wir können ein Histogramm verwenden, um die Wahrscheinlichkeitsverteilung zu visualisieren:

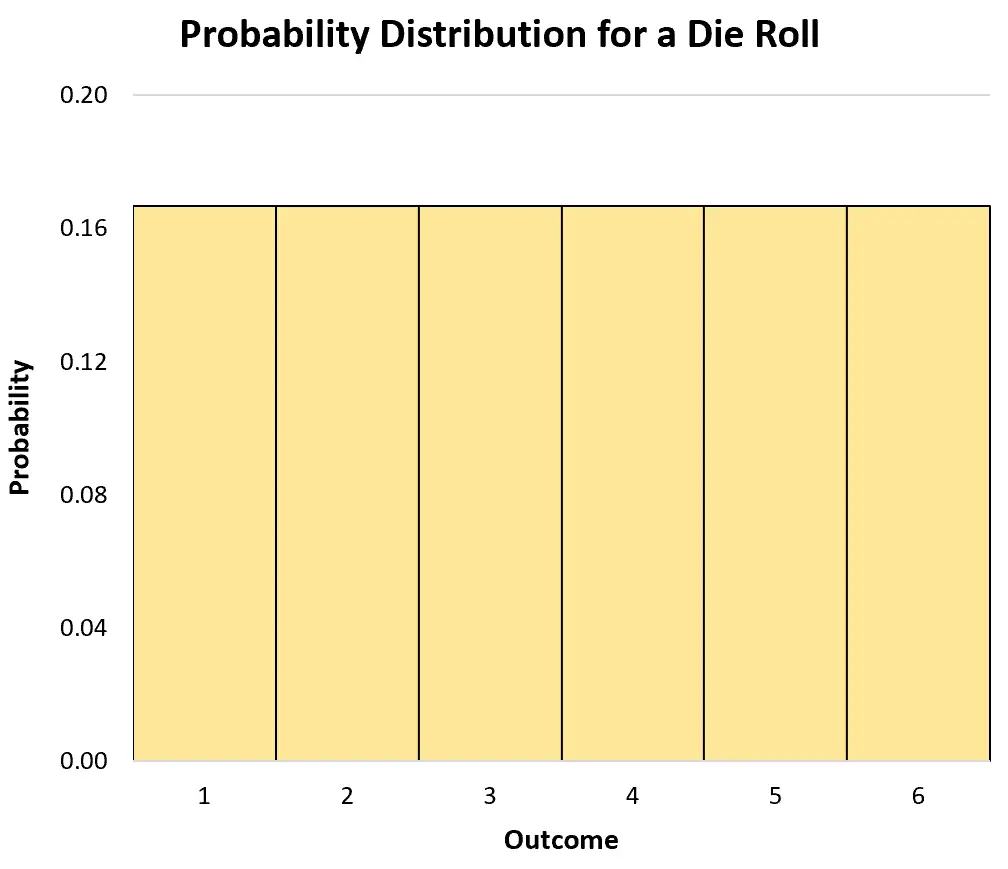
Eine kumulative Wahrscheinlichkeitsverteilung für eine diskrete Zufallsvariable gibt uns die Wahrscheinlichkeit an, mit der die Variable einen Wert annimmt , der kleiner oder gleich einem bestimmten Wert ist.

Die kumulative Wahrscheinlichkeitsverteilung für einen Würfelwurf würde beispielsweise so aussehen:

• P(X≤1): 1/6
• P(X≤2): 2/6
• P(X≤3): 3/6
• P(X≤4): 4/6
• P(X≤5): 5/6
• P(X≤6): 6/6

Die Wahrscheinlichkeit, dass der Würfel auf einer oder weniger landet, beträgt einfach 1/6, da er nicht auf einer Zahl kleiner als eins landen kann.

Die Wahrscheinlichkeit, dass es auf zwei oder weniger landet, beträgt P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6.

Ebenso ist die Wahrscheinlichkeit, dass es auf drei oder weniger landet, P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6, Und bald.

Wir können auch ein Histogramm verwenden, um die kumulative Wahrscheinlichkeitsverteilung zu visualisieren:

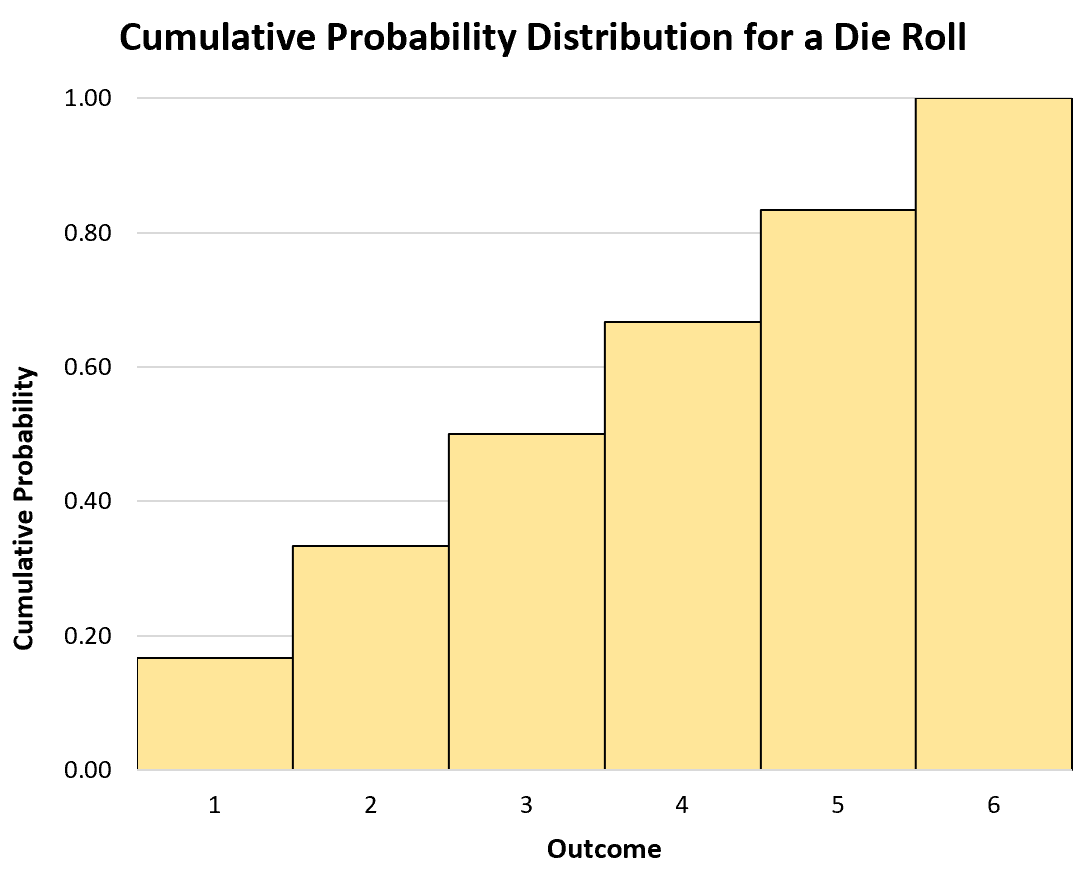
Kontinuierliche Zufallsvariablen

Eine kontinuierliche Zufallsvariable ist eine Variable, die unendlich viele mögliche Werte annehmen kann. Hier sind einige Beispiele für kontinuierliche Zufallsvariablen:

• Gewicht eines Tieres
• Größe einer Person
• Die benötigte Zeit, um einen Marathon zu laufen

Die Körpergröße einer Person könnte beispielsweise 60,2 Zoll, 65,2344 Zoll, 70,431222 Zoll usw. betragen. Es gibt unendlich viele mögliche Werte für die Größe.

Allgemeine Regel:

Wenn Sie die Anzahl der Ergebnisse zählen können, dann arbeiten Sie mit einer diskreten Zufallsvariablen – zum Beispiel zählen Sie, wie oft eine Münze „Kopf“ zeigt.

Wenn Sie das Ergebnis jedoch messen können, arbeiten Sie mit einer kontinuierlichen Zufallsvariablen – zum Beispiel mit der Messung von Größe, Gewicht, Zeit usw.

Eine Wahrscheinlichkeitsverteilung für eine kontinuierliche Zufallsvariable gibt uns die Wahrscheinlichkeit an, mit der die Zufallsvariable bestimmte Werte annimmt.

Im Gegensatz zu einer Wahrscheinlichkeitsverteilung für diskrete Zufallsvariablen kann eine Wahrscheinlichkeitsverteilung für eine kontinuierliche Zufallsvariable jedoch nur verwendet werden, um die Wahrscheinlichkeit anzugeben, mit der die Variable einen Wertebereich annimmt.

Angenommen, wir möchten die Wahrscheinlichkeit wissen, dass ein Hamburger aus einem bestimmten Restaurant ein Viertel Pfund (0,25 Pfund) wiegt. Da das Gewicht eine kontinuierliche Variable ist, kann es unendlich viele Werte annehmen.

Beispielsweise könnte ein bestimmter Hamburger tatsächlich 0,250001 Pfund, 0,24 Pfund oder 0,2488 Pfund wiegen. Die Wahrscheinlichkeit, dass ein bestimmter Hamburger genau 0,25 Pfund wiegt, ist praktisch Null.

Wir können also nur eine Wahrscheinlichkeitsverteilung verwenden, um die Wahrscheinlichkeit anzugeben, dass ein Hamburger weniger als 0,25 Pfund, mehr als 0,25 Pfund wiegt oder in einem bestimmten Bereich (z. B. zwischen 0,23 Pfund und 0,27 Pfund) wiegt.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Zufallsvariablen:

Was sind iid-Zufallsvariablen?
10 Beispiele für Zufallsvariablen im wirklichen Leben