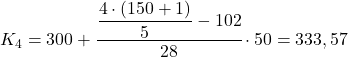Quintile (statistik)

In diesem Artikel erklären wir, was Quintile sind und wie sie berechnet werden. Sie finden mehrere gelöste Beispiele zur Berechnung von Quintilen und können darüber hinaus die Quintile jeder statistischen Stichprobe mit einem Online-Rechner berechnen.

Was sind Quintile?

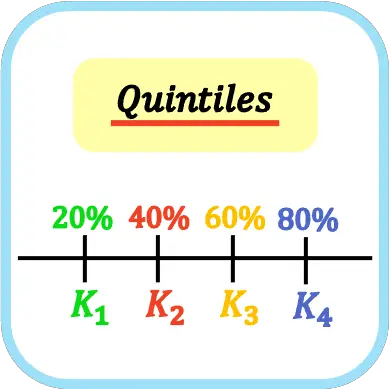
Quintile sind in der Statistik vier Werte, die einen Datensatz in fünf gleiche Teile unterteilen. Somit repräsentieren das erste, zweite, dritte und vierte Quintil 20 %, 40 %, 60 % bzw. 80 % der Stichprobendaten.

Das heißt, der Wert des dritten Quintils ist beispielsweise höher als 60 % aller erfassten Daten, aber niedriger als der Rest der Daten.

Das Symbol für Quintile ist der Großbuchstabe K mit dem Quintilindex, dh das erste Quintil ist K ₁ , das zweite Quintil ist K ₂ , das dritte Quintil ist K ₃ und das vierte Quintil ist K ₄ . Allerdings kann es auch durch den Buchstaben Q dargestellt werden (nicht empfohlen, da es zu Verwechslungen mit Quartilen führt).

👉 Mit dem Rechner unten können Sie Quintile für jeden Datensatz berechnen.

Quintile sind zusammen mit Quartilen, Dezilen und Perzentilen ein Maß für die nicht zentrale Position. Wenn Sie mehr Interesse haben, können Sie auf unserer Website nachsehen, was jeder dieser Quantiltypen bedeutet.

Es ist zu beachten, dass Quintil möglicherweise eine andere Definition hat. In der Wirtschaft stellen Quintile den Prozentsatz einer Bevölkerung dar, geordnet nach Einkommen, oder mit anderen Worten, sie ordnen eine Bevölkerung nach Einkommensniveau. Beispielsweise entspricht das erste Quintil den ärmsten 20 % der Bevölkerung einer Bevölkerung, das zweite Quintil den 40 % der Bevölkerung mit dem niedrigsten Einkommen und so weiter.

So berechnen Sie Quintile

Um die Position der Quintile einer Stichprobe oder statistischen Grundgesamtheit zu berechnen , müssen Sie die Anzahl der Quintile mit der Summe der Gesamtzahl der Daten plus eins multiplizieren und das Ergebnis durch fünf dividieren.

Daher lautet die Formel für Quintile :

Bitte beachten Sie: Das Ergebnis dieser Formel sagt uns die Position des Quintils, nicht seinen Wert. Das Quintil sind daher die Daten, die sich an der durch die Formel ermittelten Position befinden.

Manchmal liefert uns das Ergebnis dieser Formel jedoch eine Dezimalzahl. Daher müssen wir zwei Fälle unterscheiden, je nachdem, ob das Ergebnis eine Dezimalzahl ist oder nicht:

• Wenn das Ergebnis der Formel eine Zahl ohne Dezimalteil ist, sind die Daten, die sich an der durch die obige Formel bereitgestellten Position befinden, das Quintil.
• Wenn das Formelergebnis eine Zahl mit einem Dezimalteil ist, wird der Quintilwert mit dem folgenden Ausdruck berechnet:

Dabei sind x _i und x _i+1 die Zahlen der Positionen, zwischen denen sich die durch die erste Formel erhaltene Zahl befindet, und d ist der Dezimalteil der durch die erste Formel erhaltenen Zahl.

Wenn Sie Angst hatten, als Sie so viele Schritte zur Bestimmung der Quintile eines Datensatzes sahen, machen Sie sich keine Sorgen, es ist eigentlich ganz einfach. Lesen Sie die folgenden beiden Beispiele und Sie werden es sicherlich viel besser verstehen.

Hinweis : Die statistische Gemeinschaft ist sich immer noch nicht ganz einig darüber, wie Quintile berechnet werden. Daher finden Sie möglicherweise ein Buch, das dies etwas anders erklärt.

Beispiele zur Berechnung von Quintilen

Im Folgenden überlassen wir Ihnen zwei Schritt-für-Schritt-Übungen zum Erhalten von Quintilen aus einer Datenreihe. Damit Sie die beiden möglichen Fälle sehen können, sind die Ergebnisse in der ersten Übung nicht dezimal und in der zweiten Übung schon.

Beispiel 1

• Berechnen Sie die Quintile der folgenden Datenreihen:

Wie Sie in der obigen Erklärung gesehen haben, lautet die Formel zum Ermitteln der Position der Quintile:

Der Parameter n bezieht sich auf die Gesamtzahl der Daten, die 49 beträgt. Um die Position des ersten Quintils zu finden, müssen wir n durch 49 und k durch 1 ersetzen:

Aus der Formel haben wir die Zahl 10 erhalten, was bedeutet, dass sich das Quintil an der zehnten Position der geordneten Liste befindet, was den Daten 205 entspricht.

Um das zweite Quintil zu berechnen, müssen Sie dieselbe Formel verwenden, aber k durch 2 ersetzen:

Das zweite Quintil steht somit auf Position 20 der geordneten Liste, also dem Wert 236.

Nochmals wiederholen wir den Vorgang, um Quintil 3 zu bestimmen, aber logischerweise ersetzen wir jetzt das k durch 3:

Das dritte Quintil sind somit die Daten auf Position 30, was 266 entspricht.

Abschließend wenden wir die Formel noch einmal an, um das vierte Quintil zu berechnen:

Das vierte Quintil liegt somit auf Position 40, das vierte Quintil ist also 286.

Beispiel 2

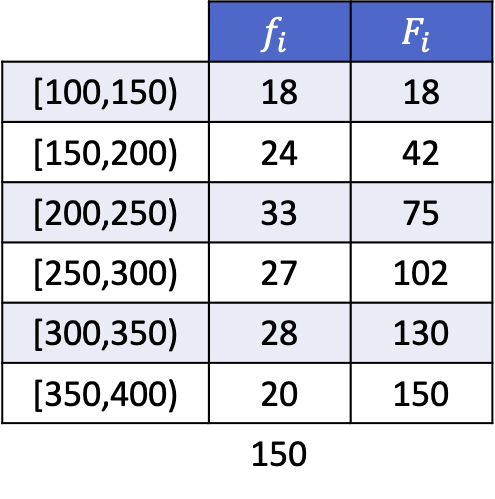
• Berechnen Sie die vier Quintile der in der folgenden Tabelle gesammelten statistischen Daten:.

Um die Positionen der Quintile zu ermitteln, müssen Sie auf die gleiche Weise wie im vorherigen Beispiel die folgende Formel verwenden:

In diesem Fall beträgt die Stichprobengröße 42 Beobachtungen. Um die Position des ersten Quintils zu ermitteln, müssen wir den Parameter n durch 42 und k durch 1 ersetzen:

Anders als im ersten Beispiel liefert uns die Formel dieses Mal jedoch eine Dezimalzahl, sodass wir die folgende Formel anwenden müssen, um das genaue Quintil zu berechnen:

Die aus der ersten Formel erhaltene Zahl beträgt 8,6, sodass das erste Quintil zwischen den achten und neunten Daten liegt, die 78 bzw. 79 betragen. Daher ist x _i 78, x _i+1 ist 79 und d ist der Dezimalteil der erhaltenen Zahl, also 0,6.

Jetzt wiederholen wir genau das gleiche Verfahren, um das zweite Quintil zu finden. Wir berechnen zunächst seine Position:

Aber aus der Formel erhalten wir eine Dezimalzahl zwischen 17 und 18, sodass das zweite Quintil zwischen der siebzehnten und achtzehnten Stelle liegt, deren Werte jeweils 109 und 112 der geordneten Liste entsprechen. Daher wenden wir im Verfahren die zweite Formel an, um den genauen Quintilwert zu ermitteln:

Wir wiederholen die Methode, um das dritte Quintil zu erhalten. Zuerst bestimmen wir seine Position:

Die berechnete Zahl 25,8 bedeutet, dass der Quintilwert zwischen der fünfundzwanzigsten und sechsundzwanzigsten Stelle liegen wird, deren Werte 134 und 141 sind. Die Berechnung des genauen Quintilwerts lautet daher:

Abschließend wiederholen wir den gleichen Vorgang ein letztes Mal, um Quintil 4 zu berechnen. Zuerst ermitteln wir seine Position:

Der genaue Wert des vierten Quintils wird daher zwischen 34 und 35 liegen, dessen Positionen den Daten 172 und 179 entsprechen. Die Berechnung des vierten Quintils lautet daher:

Quintilrechner

Geben Sie einen statistischen Datensatz in den folgenden Rechner ein, um Quintile zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Quintile in gruppierten Daten

Um Quintile zu berechnen, wenn Daten in Intervalle gruppiert sind, müssen Sie zunächst ihr Intervall oder ihre Klasse mithilfe der folgenden Formel ermitteln:

Das Quintil liegt also in dem Intervall, dessen absolute Häufigkeit unmittelbar größer ist als die mit dem vorherigen Ausdruck erhaltene Zahl.

Und sobald wir das Intervall kennen, zu dem das Quintil gehört, müssen wir die folgende Formel anwenden, um den genauen Wert des Quintils zu ermitteln:

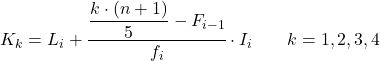
Gold:

• L _i ist die untere Grenze des Intervalls, in dem sich das Quintil befindet.
• n ist die Gesamtzahl der Beobachtungen.
• F _i-1 ist die kumulative absolute Häufigkeit des vorherigen Intervalls.
• f _i ist die absolute Häufigkeit des Intervalls, in dem sich das Quintil befindet.
• I _i ist die Breite des Quintilintervalls.

Damit Sie sehen können, wie das geht, finden Sie hier ein gelöstes Beispiel für die Berechnung der Quintile der folgenden Datenreihen, gruppiert in Intervallen:

Da die Daten gruppiert sind, müssen wir zur Berechnung von Quintilen die folgende Methode verwenden: Bestimmen Sie zunächst den Bereich, in den das Quintil fällt, und ermitteln Sie dann den genauen Wert des Quintils.

Um das Intervall zu ermitteln, in dem sich das erste Quintil befindet, verwenden wir daher die folgende Formel:

Das erste Quintil liegt in dem Intervall, dessen kumulative absolute Häufigkeit unmittelbar größer als 30,2 ist. In diesem Fall ist es das Intervall [150.200), dessen kumulative absolute Häufigkeit 42 beträgt. Und sobald wir das Quintilintervall kennen, wenden wir die zweite Formel an Verfahren zur Bestimmung des genauen Werts:

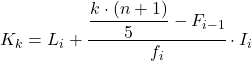
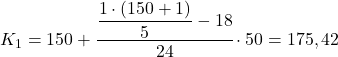
Jetzt wiederholen wir den gleichen Vorgang, um das zweite Quintil zu erhalten, indem wir zunächst das Intervall berechnen, in dem es liegt:

Die kumulative absolute Häufigkeit unmittelbar über 60,4 beträgt 75, der zweite Quintilbereich liegt also bei [200–250]. Daher setzen wir die entsprechenden Werte in die zweite Formel ein, um den genauen Quintilwert zu berechnen:

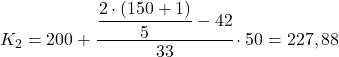
Wir führen den gleichen Vorgang ein drittes Mal durch, um Quintil 3 zu erhalten. Wir bestimmen zunächst das Intervall, in dem sich das Quintil befindet:

Das Quintil liegt im Intervall [250.300), da seine kumulative absolute Häufigkeit (102) unmittelbar über 90,6 liegt. Die Berechnung des genauen Wertes des dritten Quintils lautet daher wie folgt:

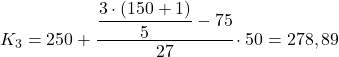
Schließlich finden wir das vierte Quintil. Wie immer ermitteln wir zunächst das Intervall:

Das Intervall, dessen absolute Häufigkeit unmittelbar größer als 120,8 ist, ist [300,350), dessen Wert 130 ist. Der genaue Wert des vierten Quintils wird daher sein: