So berechnen sie einen korrelationskoeffizienten auf einem ti-84-rechner
Ein Korrelationskoeffizient ist ein Maß für den linearen Zusammenhang zwischen zwei Variablen. Es kann einen Wert zwischen -1 und 1 annehmen, wobei:
- -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
- 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
- 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an
Mit den folgenden Schritten können Sie den Korrelationskoeffizienten zwischen zwei Variablen auf einem TI-84-Rechner berechnen:
Schritt 1: Diagnose aktivieren.
Zuerst müssen wir die Diagnose aktivieren. Drücken Sie dazu die 2. Taste und dann die Zahl 0. Dadurch gelangen wir zum KATALOG-Bildschirm.
Scrollen Sie zu „DiagnoseEin“ und drücken Sie die EINGABETASTE .
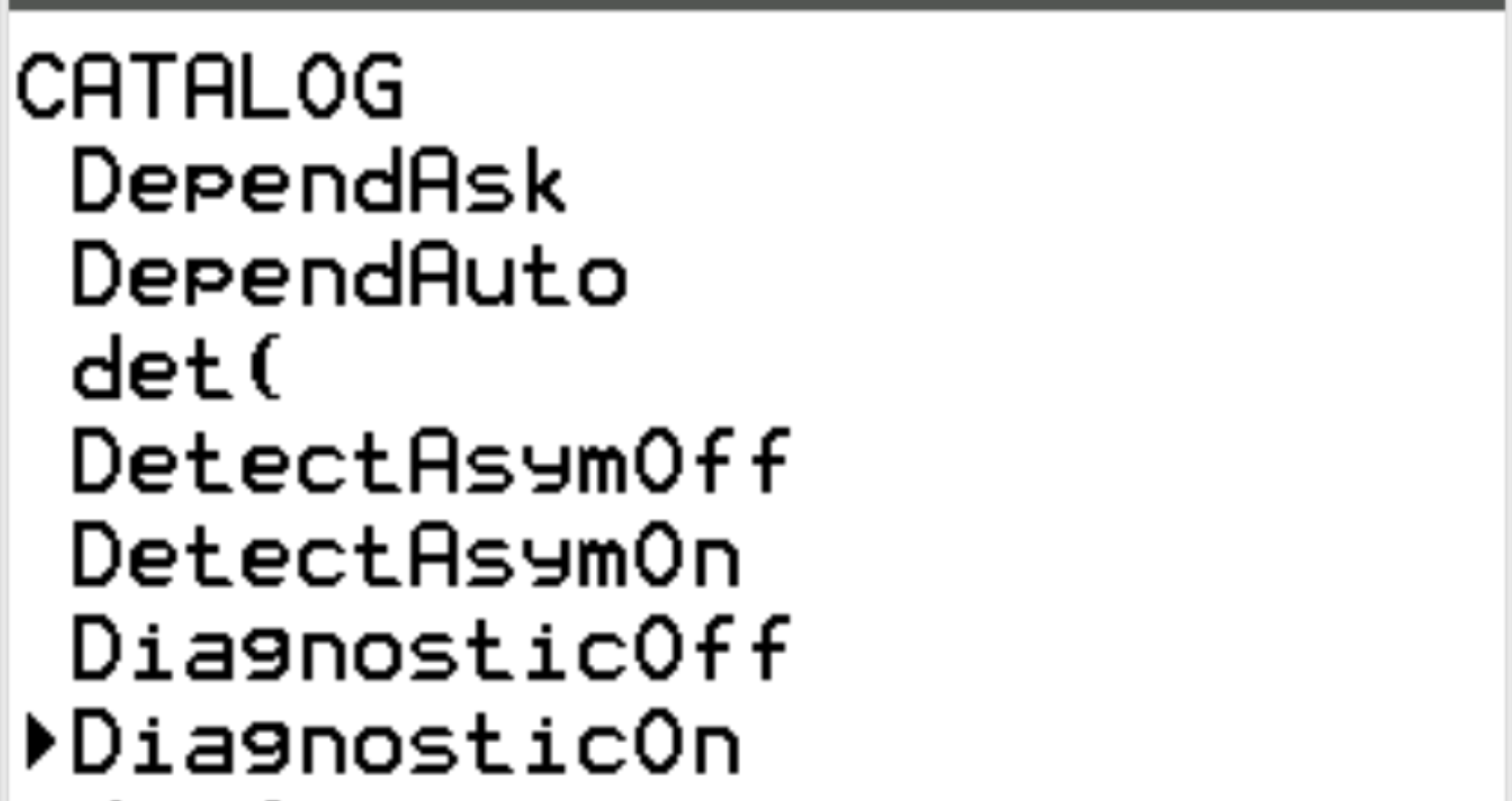
Drücken Sie dann erneut ENTER .
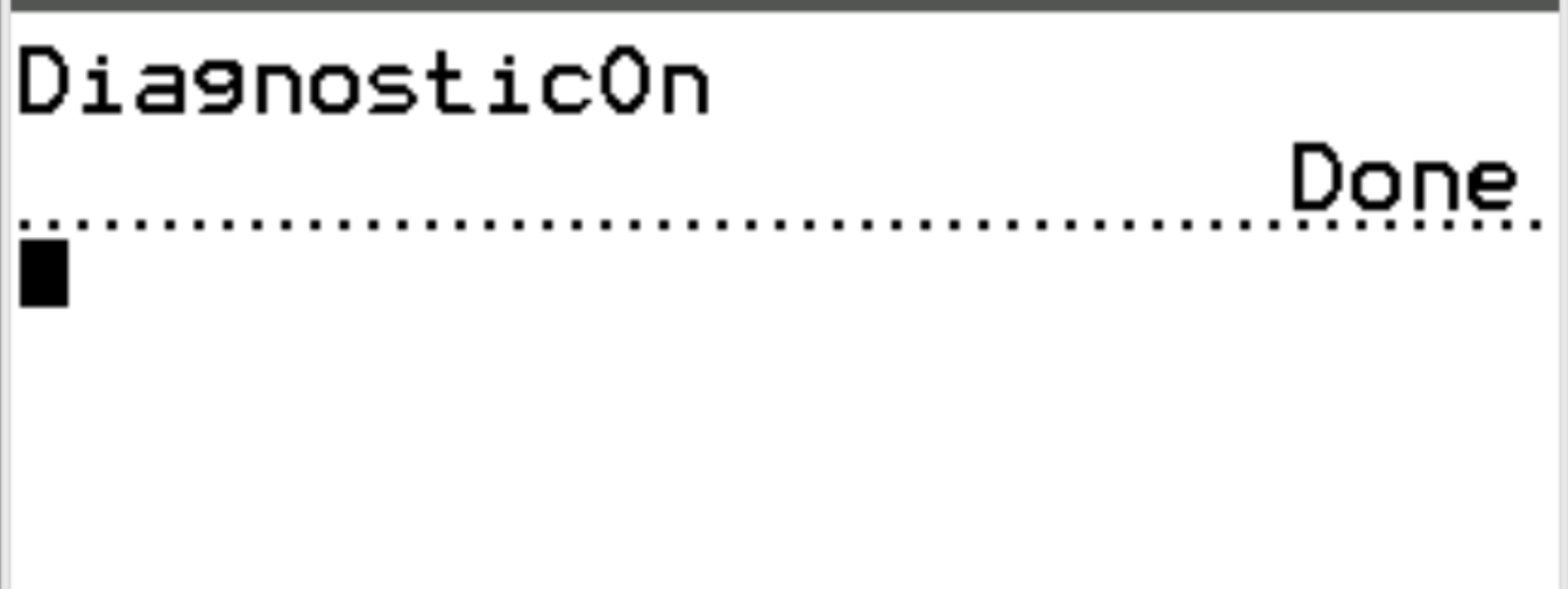
Die Diagnose ist jetzt aktiviert, sodass wir den Korrelationskoeffizienten zwischen zwei Variablen berechnen können.
Schritt 2: Geben Sie die Daten ein.
Als nächstes müssen wir die Datenwerte für unsere beiden Variablen eingeben. Drücken Sie Stat und dann EDIT . Geben Sie die Werte der ersten Variablen in Spalte L1 und die Werte der zweiten Variablen in Spalte L2 ein:
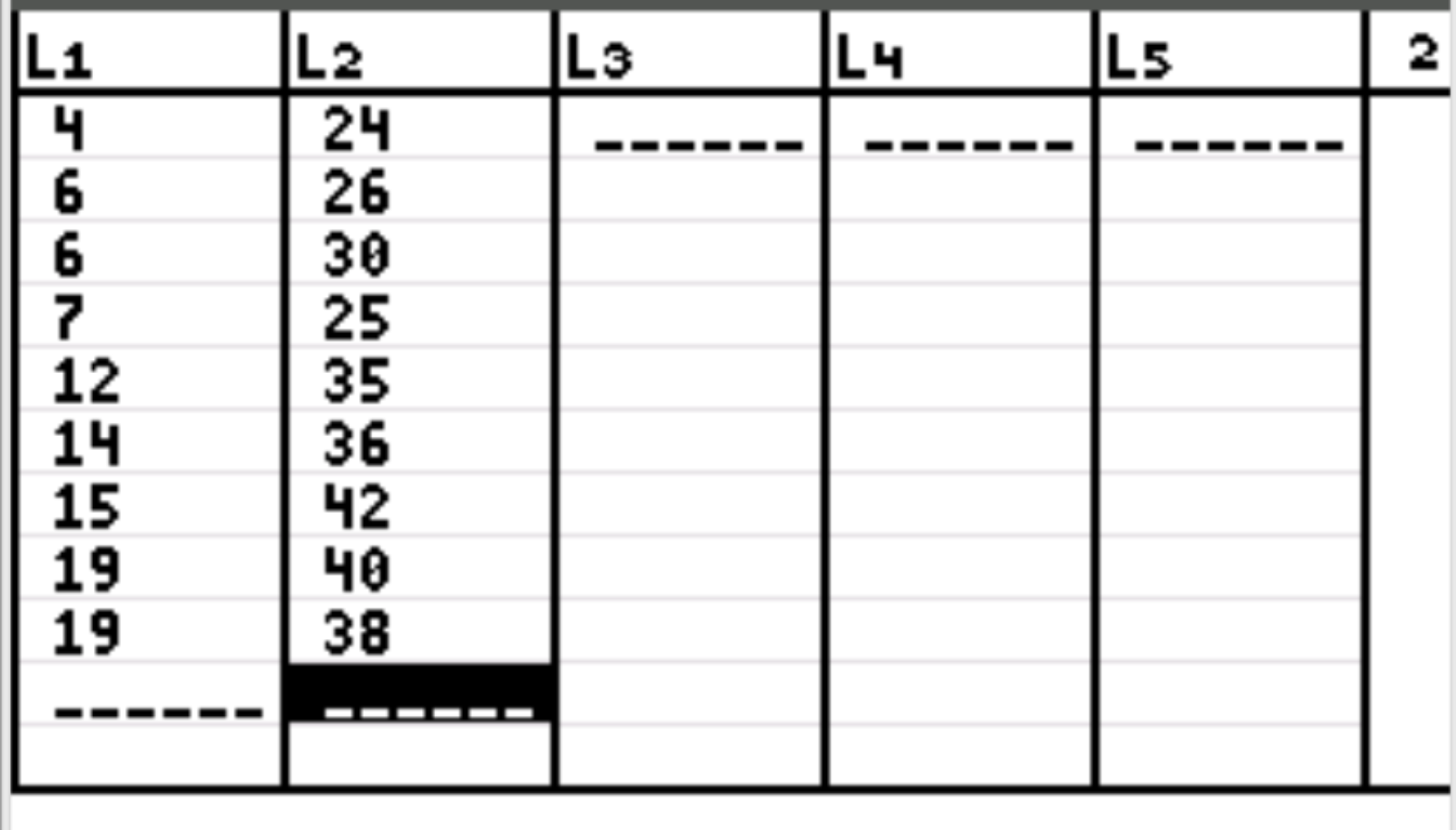
Schritt 3: Finden Sie den Korrelationskoeffizienten.
Als nächstes berechnen wir den Korrelationskoeffizienten zwischen den beiden Variablen. Drücken Sie Stat und scrollen Sie dann zu CALC . Scrollen Sie dann zu 8: Linreg(a+bx) und drücken Sie die Eingabetaste .
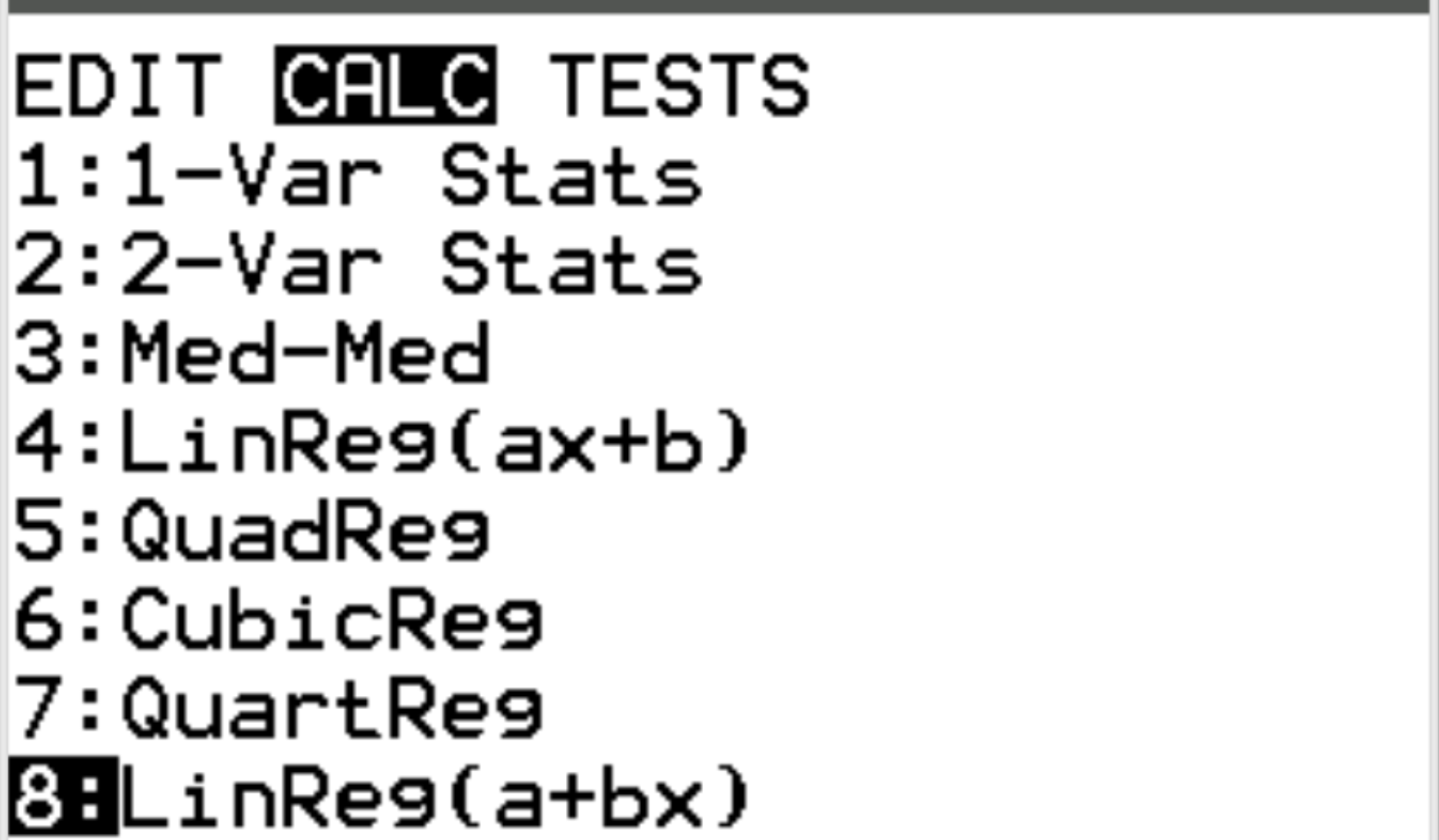
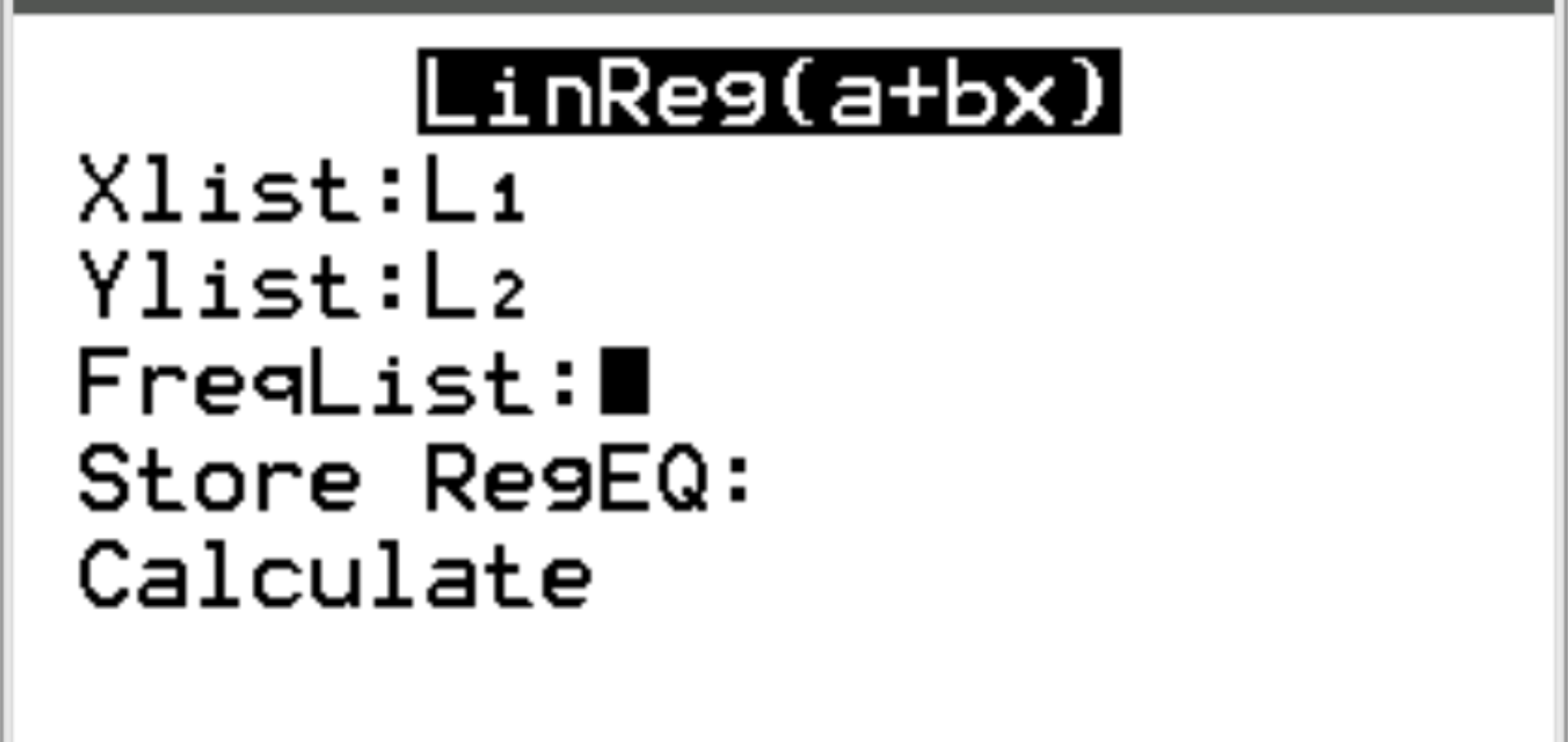
Stellen Sie sicher, dass für Xlist und Ylist L1 und L2 ausgewählt sind, da dies die Spalten sind, die wir zur Eingabe unserer Daten verwendet haben. Lassen Sie FreqList leer. Scrollen Sie nach unten zu Berechnen und drücken Sie die Eingabetaste .
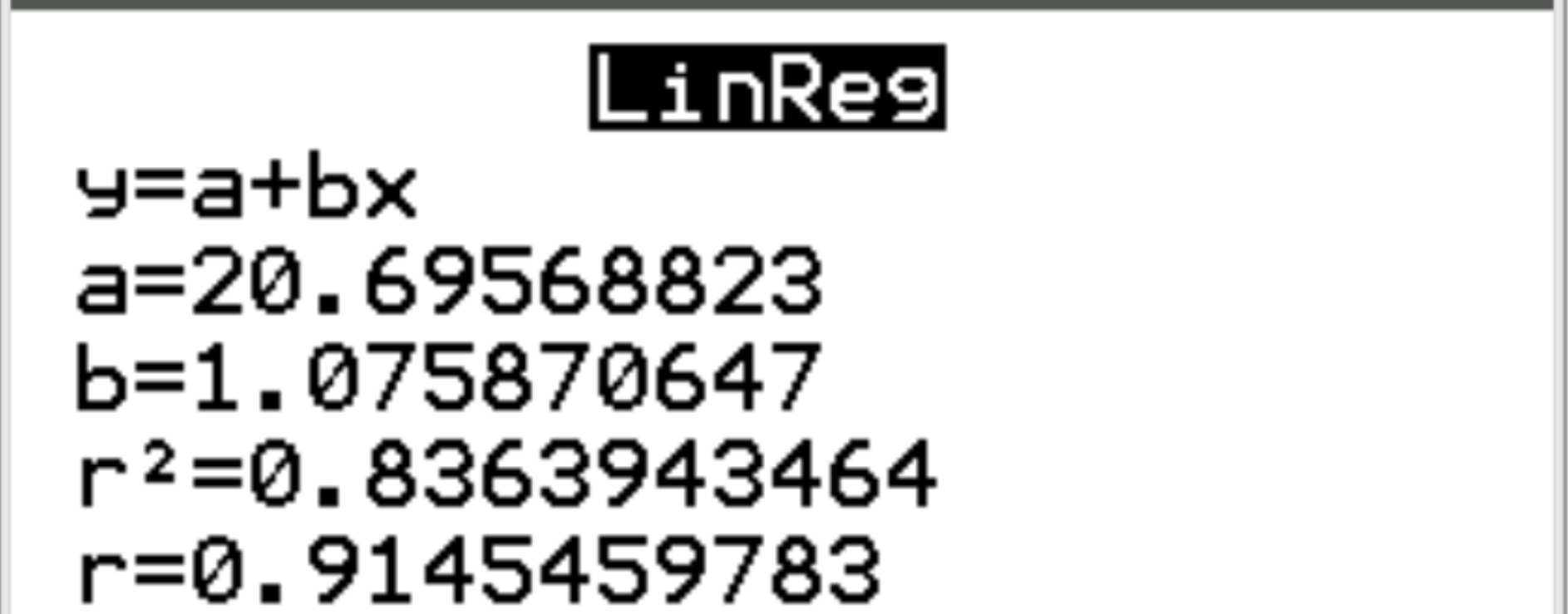
Auf dem neuen Bildschirm können wir sehen, dass der Korrelationskoeffizient (r) zwischen den beiden Variablen 0,9145 beträgt.
So interpretieren Sie einen Korrelationskoeffizienten
Die folgende Tabelle zeigt die Faustregel zur Interpretation der Stärke der Beziehung zwischen zwei Variablen basierend auf dem Wert von r :
| Absoluter Wert von r | Stärke der Beziehung |
|---|---|
| r < 0,25 | Keine Beziehung |
| 0,25 < r < 0,5 | Schwache Beziehung |
| 0,5 < r < 0,75 | Moderate Beziehungen |
| r > 0,75 | Starke Beziehung |
In unserem Beispiel weist ein Korrelationskoeffizient von 0,9145 auf eine starke positive Beziehung zwischen den beiden Variablen hin.
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen