So führen sie eine lineare regression auf einem ti-84-rechner durch

Die lineare Regression ist eine Methode, mit der wir die Beziehung zwischen einer erklärenden Variablen x und einer Antwortvariablen y verstehen können.

In diesem Tutorial wird erläutert, wie Sie eine lineare Regression auf einem TI-84-Rechner durchführen.

Beispiel: lineare Regression auf einem TI-84-Rechner

Angenommen, wir möchten den Zusammenhang zwischen der Anzahl der Stunden, die ein Student für eine Prüfung lernt, und der Note, die er bei der Prüfung erhält, verstehen.

Um diesen Zusammenhang zu untersuchen, können wir die folgenden Schritte auf einem TI-84-Rechner ausführen, um eine einfache lineare Regression durchzuführen, wobei wir die untersuchten Stunden als erklärende Variable und die Prüfungsnote als Antwortvariable verwenden.

Schritt 1: Geben Sie die Daten ein.

Zuerst geben wir die Datenwerte für die erklärende Variable und die Antwortvariable ein. Drücken Sie Stat und dann EDIT . Geben Sie die folgenden Werte für die erklärende Variable (Studienstunden) in Spalte L1 und die Werte für die Antwortvariable (Prüfungsergebnis) in Spalte L2 ein:

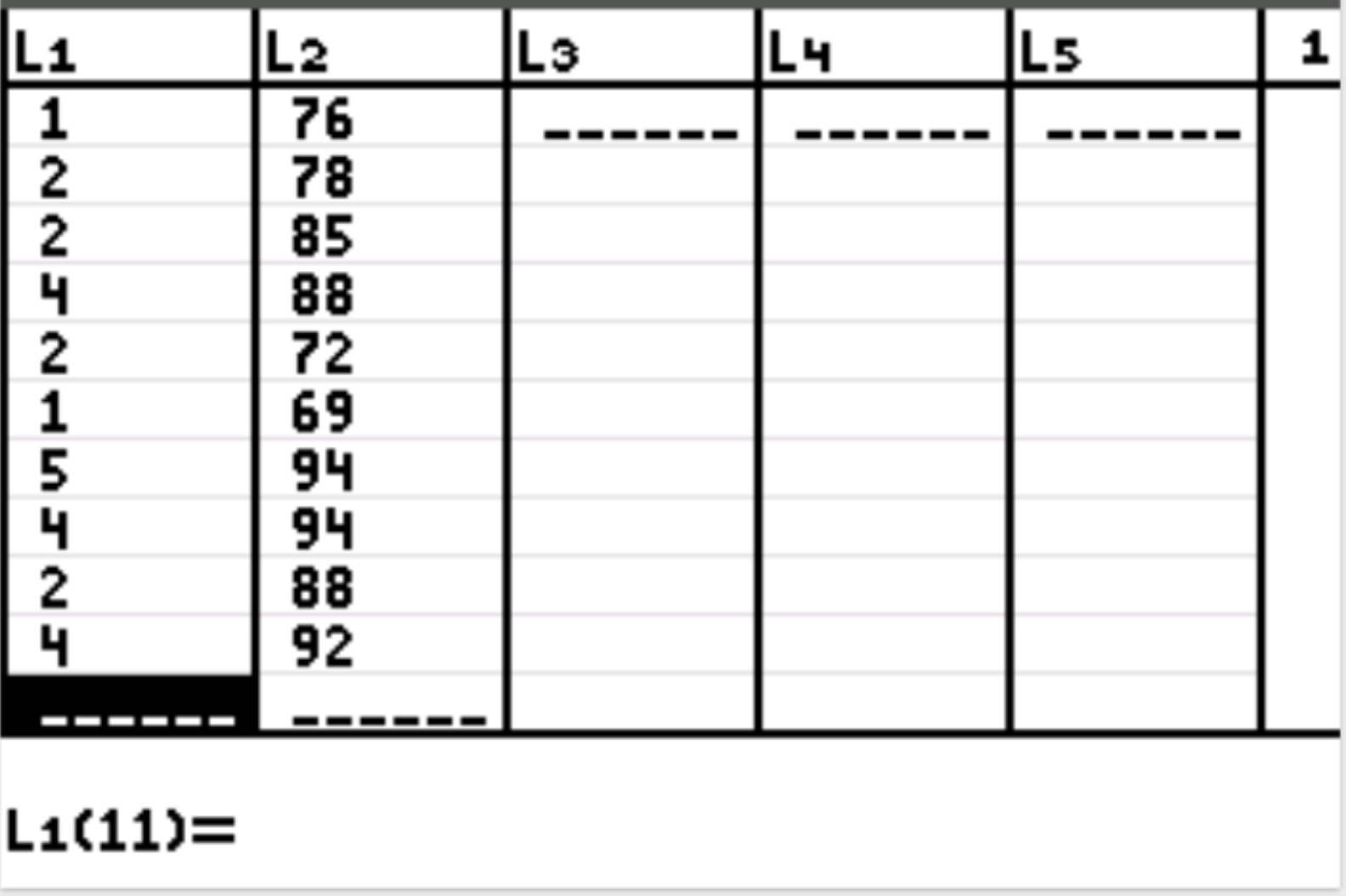
Schritt 2: Führen Sie eine lineare Regression durch.

Als nächstes führen wir eine lineare Regression durch. Drücken Sie Stat und scrollen Sie dann zu CALC . Scrollen Sie dann zu 8: Linreg(a+bx) und drücken Sie die Eingabetaste .

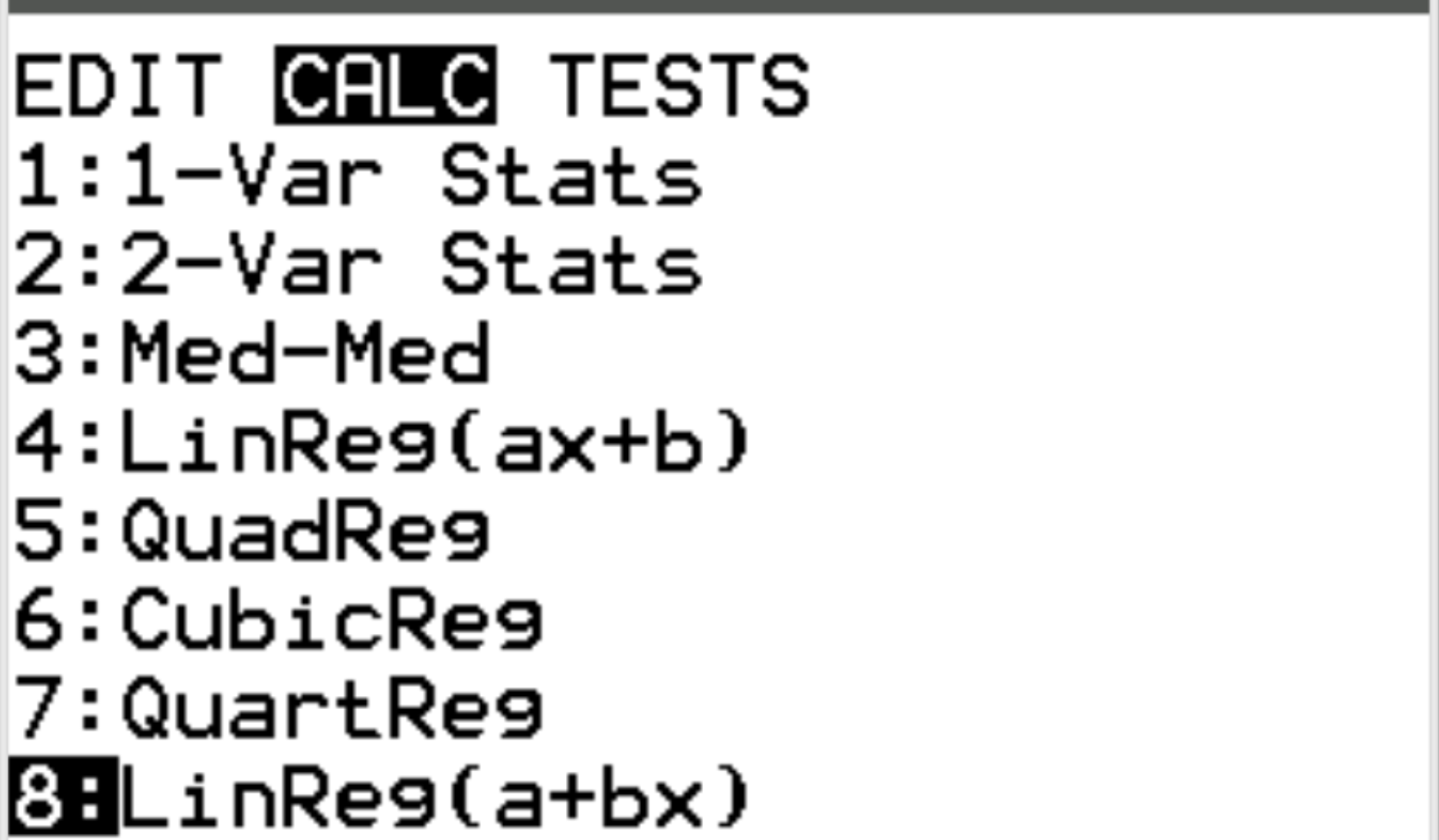
Stellen Sie sicher, dass für Xlist und Ylist L1 und L2 ausgewählt sind, da dies die Spalten sind, die wir zur Eingabe unserer Daten verwendet haben. Lassen Sie FreqList leer. Scrollen Sie nach unten zu Berechnen und drücken Sie die Eingabetaste . Es erscheint automatisch folgende Ausgabe:

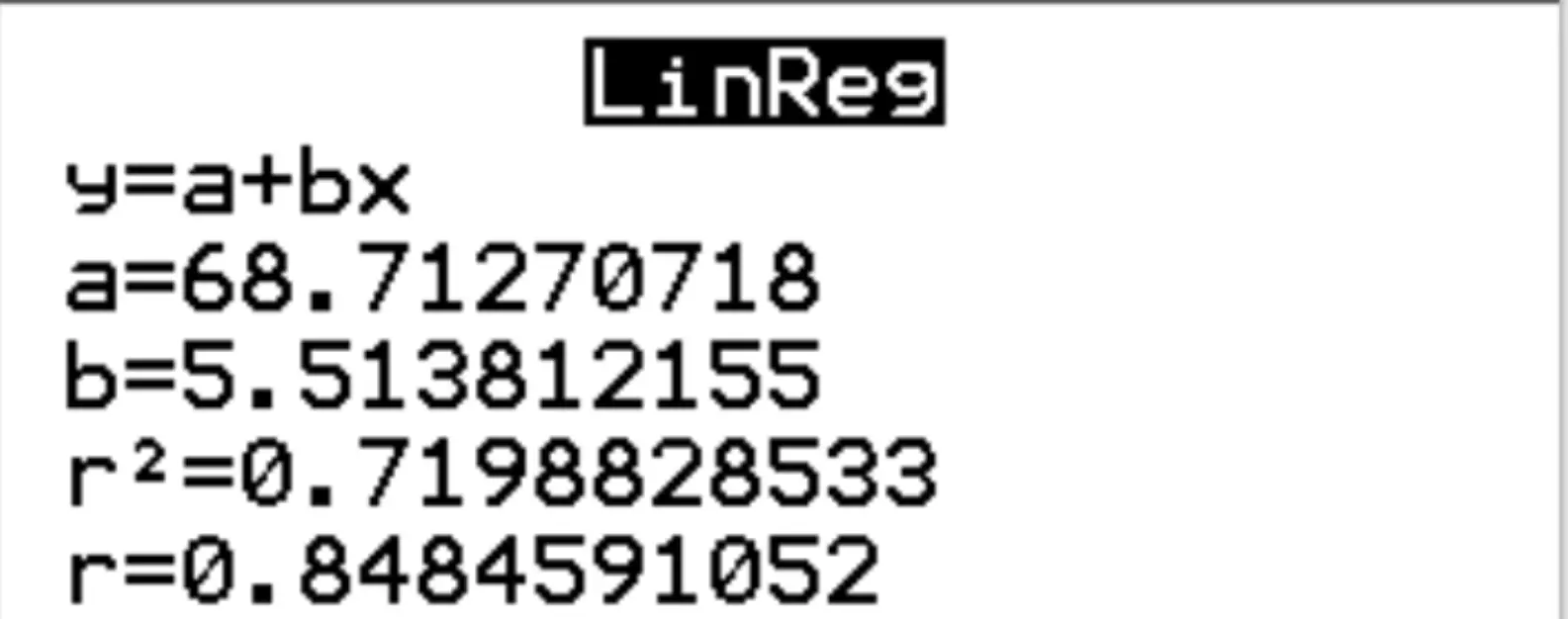
Schritt 3: Interpretieren Sie die Ergebnisse.

Aus den Ergebnissen können wir ersehen, dass die geschätzte Regressionsgleichung lautet:

Prüfungsergebnis = 68,7127 + 5,5138*(Stunden)

Wir interpretieren den Stundenkoeffizienten so, dass sich die Prüfungspunktzahl für jede weitere gelernte Stunde im Durchschnitt um 5,5138 erhöhen sollte. Wir interpretieren den Koeffizienten des Achsenabschnitts so, dass die erwartete Prüfungspunktzahl für einen Studenten, der null Stunden studiert, 68,7127 beträgt.

Mit dieser geschätzten Regressionsgleichung können wir die erwartete Prüfungspunktzahl eines Studenten basierend auf der Anzahl der Lernstunden berechnen.

Beispielsweise sollte ein Student, der drei Stunden lernt, eine Prüfungspunktzahl von 85,25 erreichen:

Prüfungsergebnis = 68,7127 + 5,5138*(3) = 85,25

Wir können auch sehen, dass das r-Quadrat für das Regressionsmodell r ² = 0,7199 ist.

Dieser Wert wird als Bestimmtheitsmaß bezeichnet. Es ist der Anteil der Varianz der Antwortvariablen, der durch die erklärende Variable erklärt werden kann. In diesem Beispiel können 71,99 % der Abweichungen bei den Prüfungsergebnissen durch die Anzahl der gelernten Stunden erklärt werden.

Zusätzliche Ressourcen

So erstellen Sie ein Residuendiagramm auf einem TI-84-Rechner
So führen Sie eine quadratische Regression auf einem TI-84-Rechner durch
So führen Sie eine exponentielle Regression auf einem TI-84-Rechner durch
So führen Sie eine logarithmische Regression auf einem TI-84-Rechner durch