So lesen sie die binomialverteilungstabelle

Die Binomialverteilungstabelle   ist eine Tabelle, die die mit der Binomialverteilung verbundenen Wahrscheinlichkeiten zeigt. Um die Binomialverteilungstabelle zu verwenden, benötigen Sie nur drei Werte:

• n: die Anzahl der Versuche
• r: die Anzahl der „Erfolge“ bei n Versuchen
• p: die Erfolgswahrscheinlichkeit eines bestimmten Versuchs

Mithilfe dieser drei Zahlen können Sie mithilfe der Binomialverteilungstabelle die Wahrscheinlichkeit ermitteln, im Verlauf von n Versuchen genau r Erfolge zu erzielen, wenn die Erfolgswahrscheinlichkeit bei jedem Versuch p beträgt.

Die folgenden Beispiele veranschaulichen, wie die Binomialverteilungstabelle gelesen wird.

Beispiel 1

Frage: Jessica macht 60 % ihrer Freiwurfversuche. Wenn sie 6 Freiwürfe macht, wie hoch ist dann die Wahrscheinlichkeit, dass sie genau 4 macht?

Um diese Frage zu beantworten, können wir den Wert in der Binomialverteilungstabelle finden, der n = 6, r = 4 und p = 0,60 entspricht:

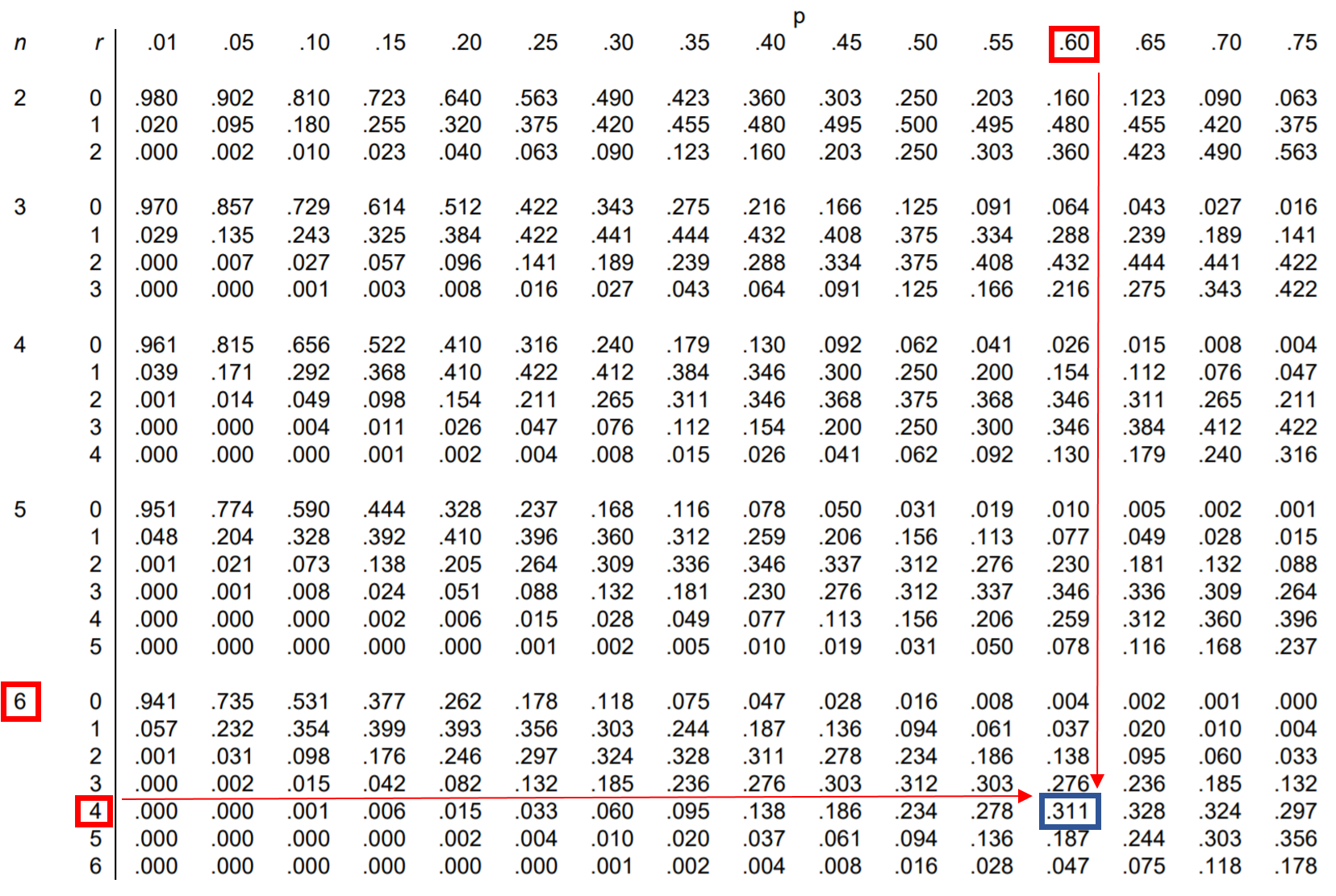
Die Wahrscheinlichkeit, dass Jessica genau 4 von 6 Freiwürfen macht, beträgt 0,311 .

Beispiel 2

Frage: Jessica macht 60 % ihrer Freiwurfversuche. Wenn sie 6 Freiwürfe macht, wie groß ist die Wahrscheinlichkeit, dass sie weniger als 4 macht?

Um diese Wahrscheinlichkeit zu ermitteln, müssen Sie tatsächlich die folgenden Wahrscheinlichkeiten hinzufügen:

P(ergibt weniger als 4) = P(ergibt 0) + P(ergibt 1) + P(ergibt 2) + P(ergibt 3)

Wir können also jede dieser vier Wahrscheinlichkeiten in der Binomialverteilungstabelle nachschlagen und sie addieren:

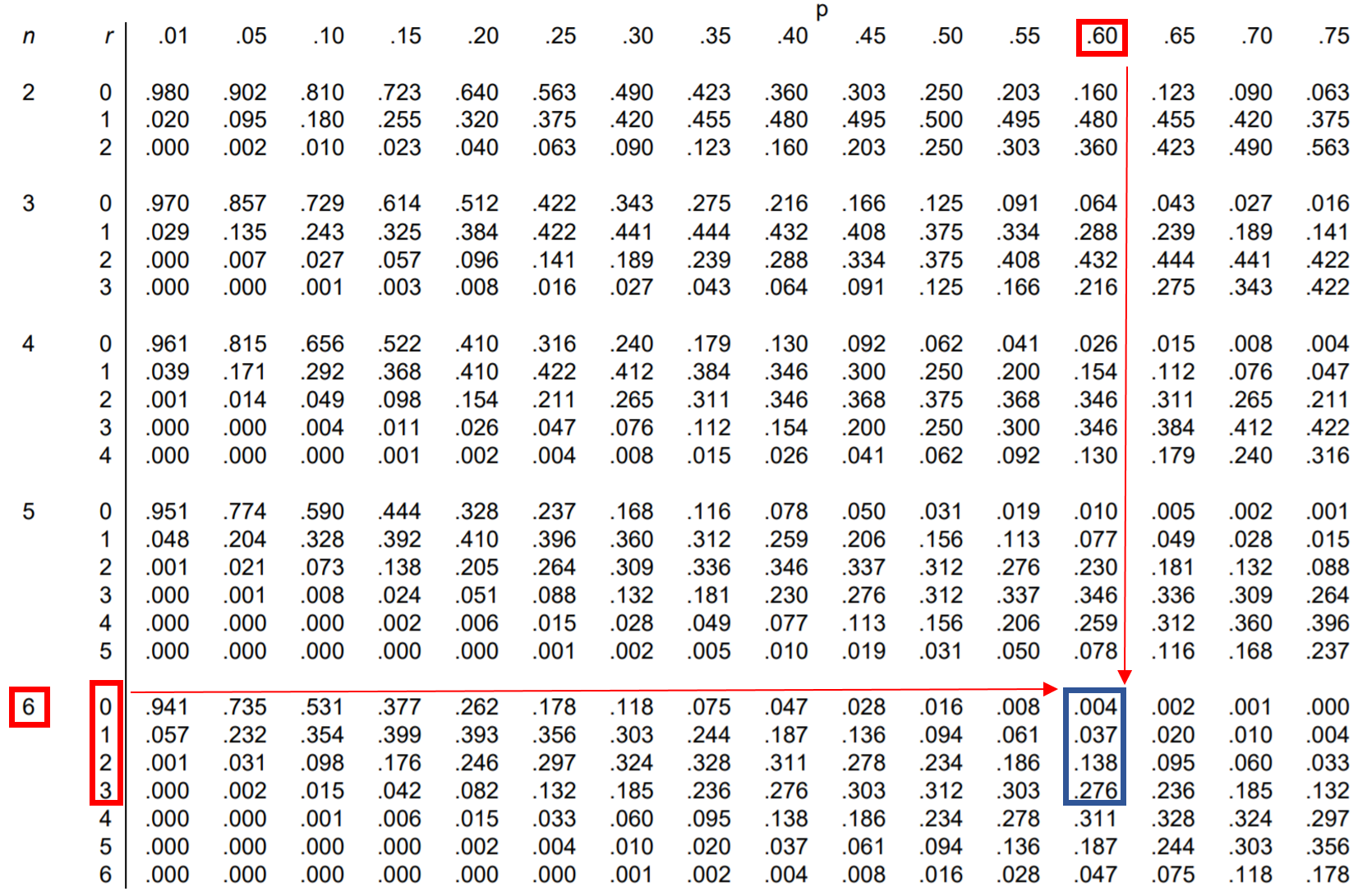
Aus der Tabelle geht hervor, dass P(ist kleiner als 4) = .004 + .037 + .138 + .276 = 0.455 .

Die Wahrscheinlichkeit, dass Jessica weniger als 4 Freiwürfe macht, beträgt 0,455 .

Beispiel 3

Frage: Jessica macht 60 % ihrer Freiwurfversuche. Wenn sie 6 Freiwürfe macht, wie hoch ist die Wahrscheinlichkeit, dass sie 4 oder mehr macht?

Um diese Wahrscheinlichkeit zu finden, müssen wir die folgenden Wahrscheinlichkeiten hinzufügen:

P(ergibt 4 oder mehr) = P(ergibt 4) + P(ergibt 5) + P(ergibt 6)

Wir können also jede dieser drei Wahrscheinlichkeiten in der Binomialverteilungstabelle nachschlagen und sie addieren:

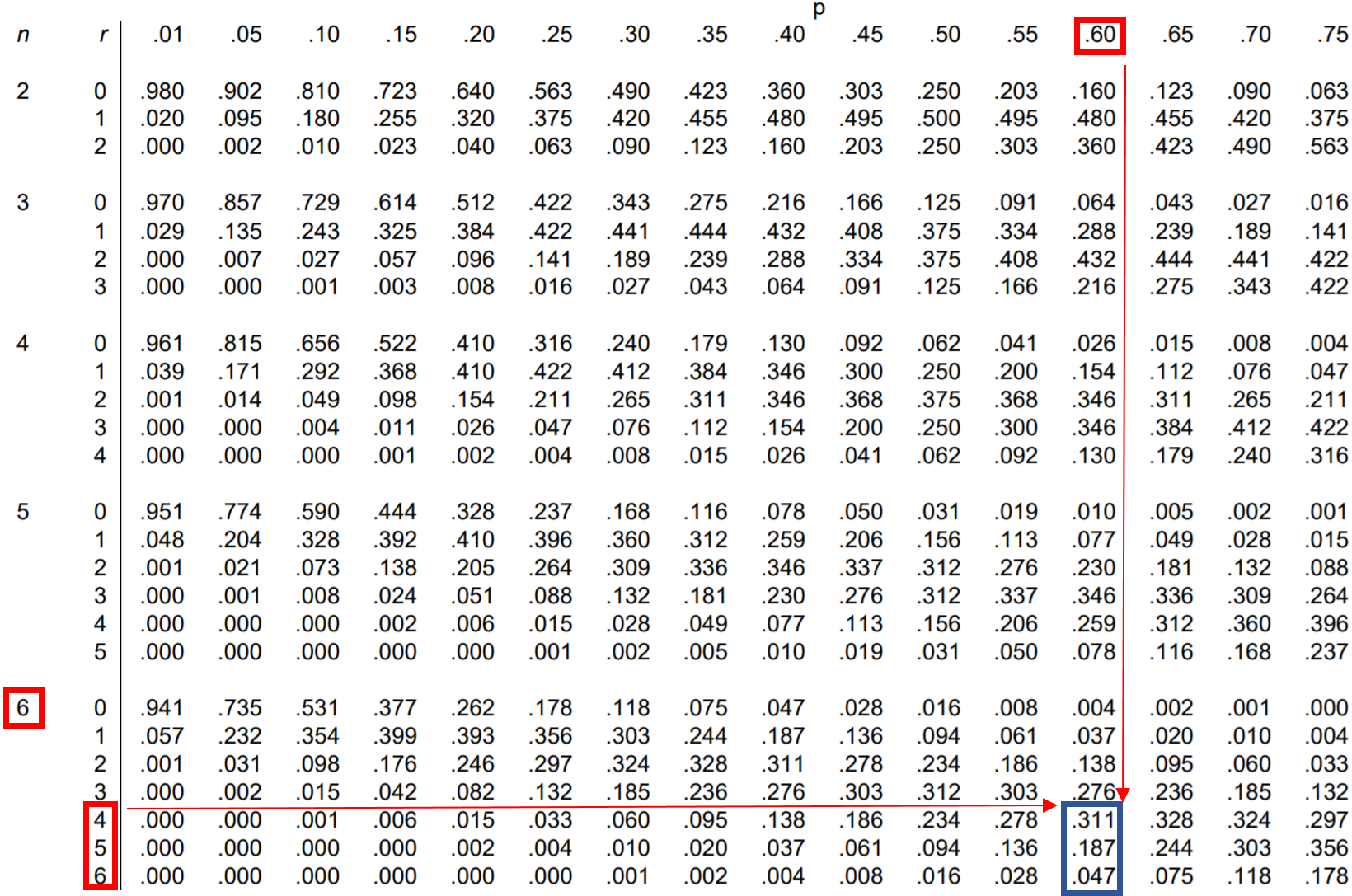
Aus der Tabelle geht hervor, dass P(ergibt 4 oder mehr) = .311 + .187 + .047 = 0.545 .

Die Wahrscheinlichkeit, dass Jessica 4 oder mehr Freiwürfe macht, beträgt 0,545 .