Konfidenzintervall für unterschiede in den proportionen
Ein Konfidenzintervall (CI) für einen Anteilsunterschied ist ein Wertebereich, der mit einem bestimmten Konfidenzniveau wahrscheinlich den wahren Unterschied zwischen zwei Bevölkerungsanteilen enthält.
In diesem Tutorial wird Folgendes erklärt:
- Die Motivation, dieses Konfidenzintervall zu erstellen.
- Die Formel zum Erstellen dieses Konfidenzintervalls.
- Ein Beispiel für die Berechnung dieses Konfidenzintervalls.
- Wie ist dieses Konfidenzintervall zu interpretieren?
CI für den Unterschied in den Proportionen: Motivation
Forscher möchten häufig den Unterschied zwischen zwei Bevölkerungsanteilen abschätzen. Um diesen Unterschied abzuschätzen, sammeln sie eine Zufallsstichprobe aus jeder Population und berechnen den Anteil für jede Stichprobe. Dann können sie den Unterschied zwischen den beiden Proportionen vergleichen.
Sie können jedoch nicht sicher wissen, ob der Unterschied zwischen den Stichprobenanteilen dem wahren Unterschied zwischen den Bevölkerungsanteilen entspricht. Aus diesem Grund können sie ein Konfidenzintervall für die Differenz zwischen den beiden Anteilen erstellen. Dies liefert einen Wertebereich, der wahrscheinlich den wahren Unterschied zwischen den Bevölkerungsanteilen enthält.
Angenommen, wir möchten den Unterschied zwischen dem Anteil der Einwohner, die ein bestimmtes Gesetz in Kreis A unterstützen, und dem Anteil, der das Gesetz in Kreis B befürwortet, schätzen.
Da es in jedem Landkreis Tausende von Einwohnern gibt, wäre es zu zeitaufwändig und teuer, jeden einzelnen Einwohner in jedem Landkreis zu befragen.
Stattdessen könnten wir eine einfache Zufallsstichprobe von Einwohnern aus jedem Kreis ziehen und den Anteil der Befürworter des Gesetzes in jeder Stichprobe verwenden, um den tatsächlichen Unterschied in den Anteilen zwischen den beiden Kreisen abzuschätzen:
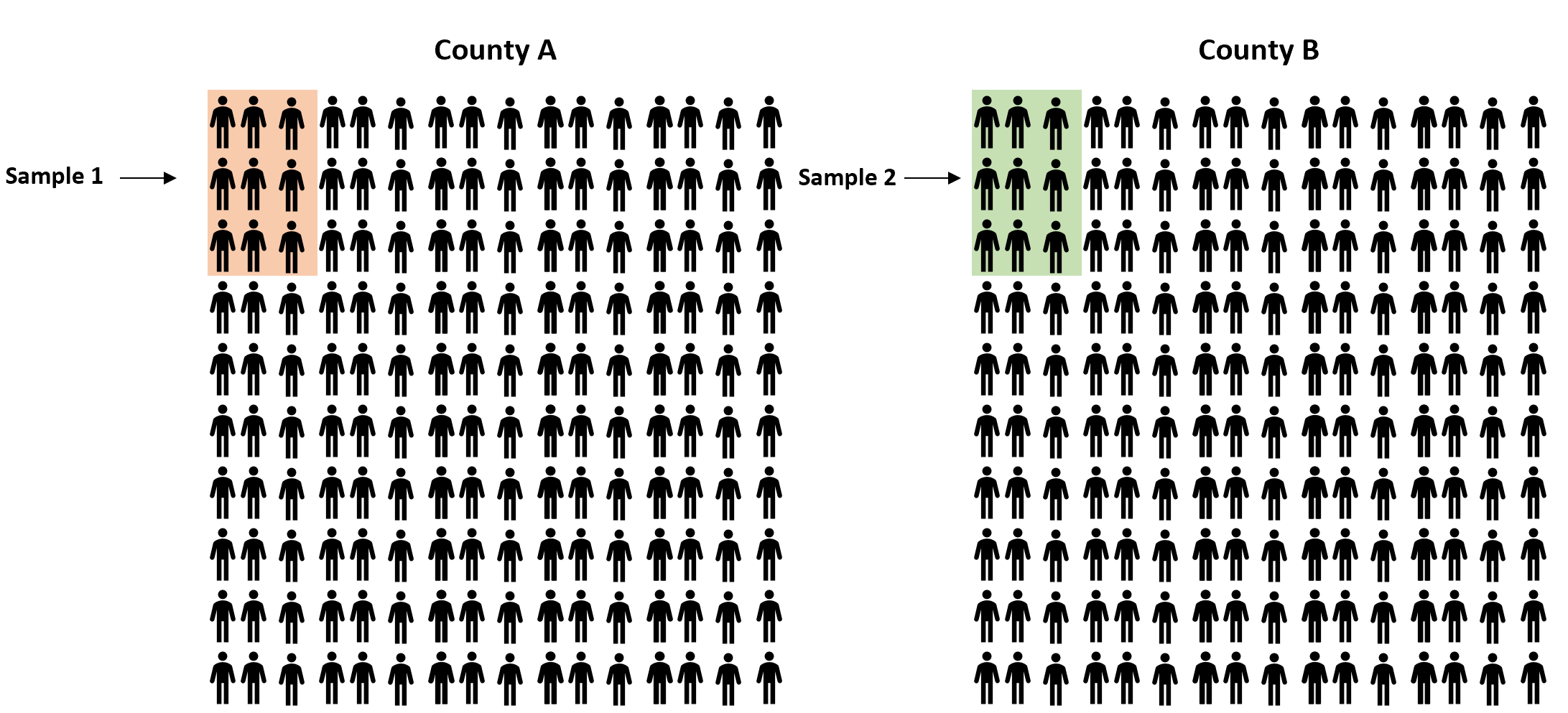
Da es sich bei unseren Stichproben um Zufallsstichproben handelt, kann nicht garantiert werden, dass der Unterschied in den Anteilen zwischen den beiden Stichproben genau dem Unterschied in den Anteilen zwischen den beiden Populationen entspricht. Um diese Unsicherheit zu erfassen, können wir ein Konfidenzintervall erstellen, das einen Wertebereich enthält, der wahrscheinlich den wahren Unterschied in den Anteilen zwischen den beiden Populationen enthält.
CI für den Unterschied in den Proportionen: Formel
Wir verwenden die folgende Formel, um ein Konfidenzintervall für eine Differenz zwischen zwei Bevölkerungsanteilen zu berechnen:
Konfidenzintervall = (p 1 – p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
Gold:
- p 1 , p 2 : Anteil von Probe 1, Anteil von Probe 2
- z: der z-kritische Wert basierend auf dem Konfidenzniveau
- n 1 , n 2 : Stichprobengröße 1, Stichprobengröße 2
Der von Ihnen verwendete Z-Wert hängt vom gewählten Konfidenzniveau ab. Die folgende Tabelle zeigt den Z-Wert, der den häufigsten Konfidenzniveauoptionen entspricht:
| Ein Maß an Selbstvertrauen | z-Wert |
|---|---|
| 0,90 | 1.645 |
| 0,95 | 1,96 |
| 0,99 | 2,58 |
Beachten Sie, dass höhere Konfidenzniveaus größeren Z-Werten entsprechen, was zu größeren Konfidenzintervallen führt. Das bedeutet, dass beispielsweise ein 95 %-Konfidenzintervall breiter ist als ein 90 %-Konfidenzintervall für denselben Datensatz.
CI für den Unterschied in den Proportionen: Beispiel
Angenommen, wir möchten den Unterschied zwischen dem Anteil der Einwohner, die ein bestimmtes Gesetz in Landkreis A unterstützen, und dem Anteil, der das Gesetz in Landkreis B unterstützt, schätzen. Hier sind die zusammenfassenden Daten für jede Stichprobe:
Probe 1:
- n 1 = 100
- p 1 = 0,62 (d. h. 62 von 100 Einwohnern unterstützen das Gesetz)
Probe 2:
- n2 = 100
- p 2 = 0,46 (d. h. 46 von 100 Einwohnern unterstützen das Gesetz)
So finden Sie unterschiedliche Konfidenzintervalle für den Unterschied in den Bevölkerungsanteilen:
90 %-Konfidenzintervall:
(.62-.46) +/- 1.645*√(.62(1-.62)/100 + .46(1-.46)/100) = [.0456, .2744]
95 %-Konfidenzintervall:
(.62-.46) +/- 1.96*√(.62(1-.62)/100 + .46(1-.46)/100) = [.0236, .2964]
99 %-Konfidenzintervall:
(0,62-0,46) +/- 2,58*√(0,62(1-0,62)/100 + 0,46(1-0,46)/100) = [-0,0192, 0,3392]
Hinweis: Sie können diese Konfidenzintervalle auch mit dem Konfidenzintervall-Rechner für Proportionsdifferenzen ermitteln.
CI für den Unterschied in den Proportionen : Interpretation
Die Art und Weise, wie wir ein Konfidenzintervall interpretieren würden, ist:
Es besteht eine Wahrscheinlichkeit von 95 %, dass das Konfidenzintervall von [.0236, .2964] den wahren Unterschied im Anteil der Einwohner, die das Gesetz unterstützen, zwischen den beiden Landkreisen enthält.
Da dieses Intervall nicht den Wert „0“ enthält, bedeutet dies, dass es sehr wahrscheinlich ist, dass es einen echten Unterschied im Anteil der Einwohner gibt, die dieses Gesetz in Landkreis A im Vergleich zu Landkreis B unterstützen.