Eine einführung in die poisson-verteilung

Die Poisson-Verteilung ist eine der beliebtesten Verteilungen in der Statistik.

Um die Poisson-Verteilung zu verstehen, ist es hilfreich, zunächst Poisson-Experimente zu verstehen.

Fischexperimente

Ein Poisson-Experiment ist ein Experiment mit den folgenden Eigenschaften:

• Die Erfolge des Experiments können gezählt werden.
• Die durchschnittliche Anzahl der Erfolge, die während eines bestimmten Zeit- (oder Raum-)Intervalls aufgetreten sind, ist bekannt.
• Jedes Ergebnis ist unabhängig.
• Die Wahrscheinlichkeit, dass ein Erfolg eintritt, ist proportional zur Größe des Intervalls.

Ein Beispiel für ein Poisson-Experiment ist die Anzahl der Geburten pro Stunde in einem bestimmten Krankenhaus. Angenommen, in einem bestimmten Krankenhaus werden durchschnittlich 10 Geburten pro Stunde durchgeführt. Dies ist ein Poisson-Experiment, da es die folgenden vier Eigenschaften aufweist:

• Die Erfolge des Experiments können gezählt werden – Wir können die Anzahl der Geburten zählen.
• Die durchschnittliche Anzahl der Geburten, die in einem bestimmten Zeitintervall stattfinden, ist bekannt – es ist bekannt, dass es durchschnittlich 10 Geburten pro Stunde gibt.
• Jedes Ergebnis ist unabhängig – Die Wahrscheinlichkeit, dass eine Mutter in einer bestimmten Stunde ein Kind zur Welt bringt, ist unabhängig von der Wahrscheinlichkeit, dass eine andere Mutter ein Kind zur Welt bringt.
• Die Erfolgswahrscheinlichkeit ist proportional zur Größe des Intervalls: Je länger das Zeitintervall, desto höher ist die Wahrscheinlichkeit, dass eine Geburt eintritt.

Wir können die Poisson-Verteilung verwenden, um Fragen zu Wahrscheinlichkeiten zu diesem Poisson-Experiment zu beantworten, wie zum Beispiel:

• Wie groß ist die Wahrscheinlichkeit, dass in einer Stunde mehr als 12 Geburten stattfinden?
• Wie hoch ist die Wahrscheinlichkeit, dass in einer bestimmten Stunde weniger als 5 Geburten stattfinden?
• Wie hoch ist die Wahrscheinlichkeit, dass in einer Stunde zwischen 8 und 11 Geburten stattfinden?

Die Fischverteilung

Die Poisson-Verteilung beschreibt die Wahrscheinlichkeit, in einem bestimmten Zeitintervall k Erfolge zu erzielen.

Wenn eine Zufallsvariable X einer Poisson-Verteilung folgt, kann die Erfolgswahrscheinlichkeit von X = k mit der folgenden Formel ermittelt werden:

P(X=k) = λ ^k * e ^{– λ} / k!

Gold:

• λ: durchschnittliche Anzahl von Erfolgen, die während eines bestimmten Intervalls auftreten
• k: Anzahl der Erfolge
• e: eine Konstante, die ungefähr 2,71828 entspricht

Angenommen, in einem bestimmten Krankenhaus gibt es durchschnittlich zwei Geburten pro Stunde. Wir können die obige Formel verwenden, um die Wahrscheinlichkeit zu bestimmen, 0, 1, 2, 3 Geburten usw. zu erleben. in einer bestimmten Stunde:

P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353

P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707

P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Wir können die Wahrscheinlichkeit beliebig vieler Geburten bis ins Unendliche berechnen. Anschließend erstellen wir ein einfaches Histogramm, um diese Wahrscheinlichkeitsverteilung zu visualisieren:

Berechnung kumulativer Poisson-Wahrscheinlichkeiten

Es ist einfach, eine einzelne Poisson-Wahrscheinlichkeit (z. B. die Wahrscheinlichkeit, dass in einem Krankenhaus drei Geburten in einer bestimmten Stunde stattfinden) mithilfe der obigen Formel zu berechnen. Um jedoch kumulative Poisson-Wahrscheinlichkeiten zu berechnen, müssen wir einzelne Wahrscheinlichkeiten addieren.

Nehmen wir zum Beispiel an, wir möchten die Wahrscheinlichkeit wissen, dass es im Krankenhaus in einer bestimmten Stunde eine oder weniger Geburten geben wird. Zur Berechnung dieser Wahrscheinlichkeit würden wir die folgende Formel verwenden:

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

Dies wird als kumulative Wahrscheinlichkeit bezeichnet, da dabei mehrere Wahrscheinlichkeiten addiert werden. Mit einer ähnlichen Formel können wir die kumulative Wahrscheinlichkeit berechnen, in einer bestimmten Stunde k oder weniger Geburten zu erleben:

P(X≤0) = P(X=0) = 0,1353

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767

Wir können diese kumulativen Wahrscheinlichkeiten für eine beliebige Anzahl von Geburten bis ins Unendliche berechnen. Anschließend können wir ein Histogramm erstellen, um diese kumulative Wahrscheinlichkeitsverteilung zu visualisieren:

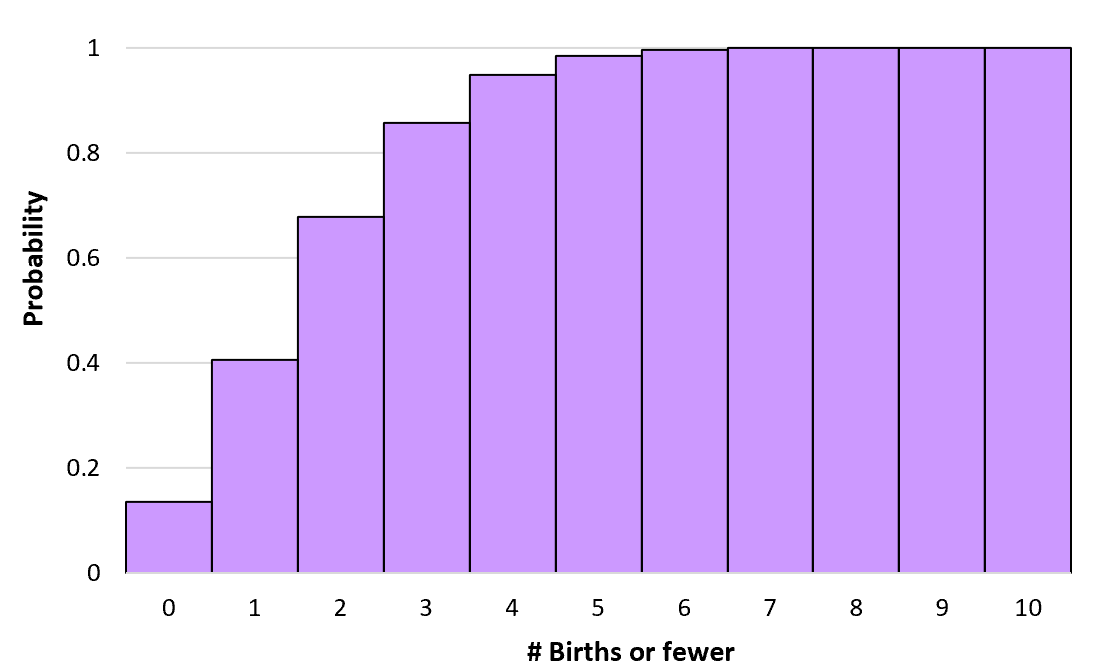
Eigenschaften der Poisson-Verteilung

Die Poisson-Verteilung hat die folgenden Eigenschaften:

Der Mittelwert der Verteilung ist λ .

Die Varianz der Verteilung beträgt ebenfalls λ .

Die Standardabweichung der Verteilung beträgt √ λ .

Angenommen, in einem Krankenhaus werden durchschnittlich zwei Geburten pro Stunde durchgeführt.

Die durchschnittliche Anzahl der in einer bestimmten Stunde erwarteten Geburten beträgt λ = 2 Geburten.

Die von uns erwartete Varianz der Geburtenzahl beträgt λ = 2 Geburten.

Probleme in der Fischverteilungspraxis

Verwenden Sie die folgenden Übungsaufgaben, um Ihr Wissen über die Poisson-Verteilung zu testen.

Hinweis: Zur Berechnung der Antworten auf diese Fragen verwenden wir den Poisson-Verteilungsrechner .

Problem 1

Frage: Wir wissen, dass eine bestimmte Website 10 Verkäufe pro Stunde tätigt. Wie groß ist die Wahrscheinlichkeit, dass die Website in einer bestimmten Stunde genau 8 Verkäufe tätigt?

Antwort: Mit dem Poisson-Verteilungsrechner mit λ = 10 und x = 8 finden wir P(X=8) = 0,1126 .

Problem 2

Frage: Wir wissen, dass ein bestimmter Immobilienmakler durchschnittlich 5 Verkäufe pro Monat tätigt. Wie groß ist die Wahrscheinlichkeit, dass sie in einem bestimmten Monat mehr als 7 Verkäufe tätigt?

Antwort: Mit dem Poisson-Verteilungsrechner mit λ = 5 und x = 7 finden wir P(X>7) = 0,13337 .

Problem 3

Frage: Wir wissen, dass in einem bestimmten Krankenhaus 4 Entbindungen pro Stunde stattfinden. Wie hoch ist die Wahrscheinlichkeit, dass es in einer bestimmten Stunde 4 oder weniger Geburten gibt?

Antwort: Unter Verwendung des Poisson-Verteilungsrechners mit λ = 4 und x = 4 finden wir, dass P(X≤4) = 0,62884 ist.

Zusätzliche Ressourcen

In den folgenden Artikeln wird erläutert, wie die Poisson-Verteilung in verschiedenen Statistikprogrammen verwendet wird:

So verwenden Sie die Poisson-Verteilung in R
So verwenden Sie die Poisson-Verteilung in Excel
So berechnen Sie Poisson-Wahrscheinlichkeiten mit einem TI-84-Rechner
Beispiele aus der Praxis der Poisson-Verteilung
Fischverteilungsrechner