Eine einführung in ancova (varianzanalyse)

ANCOVA steht für „Analyse der Kovarianz“. Um zu verstehen, wie eine ANCOVA funktioniert, ist es hilfreich, zunächst die ANOVA zu verstehen.

Eine ANOVA   (Varianzanalyse) wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht oder nicht.

Nehmen wir zum Beispiel an, wir möchten wissen, ob sich die Lerntechnik auf die Prüfungsergebnisse einer Klasse von Schülern auswirkt oder nicht. Wir haben die Klasse nach dem Zufallsprinzip in drei Gruppen eingeteilt. Jede Gruppe wendet einen Monat lang eine andere Lerntechnik an, um sich auf eine Prüfung vorzubereiten. Am Ende des Monats legen alle Studierenden die gleiche Prüfung ab.

Um herauszufinden, ob die Lerntechnik einen Einfluss auf die Prüfungsergebnisse hat, können wir eine einfache ANOVA durchführen, die uns sagt, ob es einen statistisch signifikanten Unterschied zwischen den Durchschnittsergebnissen der drei Gruppen gibt.

Eine ANCOVA ist eine Erweiterung einer ANOVA, bei der wir nach Berücksichtigung einer oder mehrerer Kovariaten bestimmen möchten, ob zwischen drei oder mehr unabhängigen Gruppen ein statistisch signifikanter Unterschied besteht.

Eine Kovariate ist eine kontinuierliche Variable, die mit der Antwortvariablen variiert.

Nehmen wir zum Beispiel an, wir möchten wissen, ob die Lerntechnik einen Einfluss auf die Prüfungsergebnisse hat, aber wir möchten die Note berücksichtigen, die der Schüler bereits in der Klasse hat . Wir können ihre aktuelle Note als Kovariate verwenden und eine ANCOVA durchführen, um festzustellen, ob zwischen den durchschnittlichen Prüfungsergebnissen der drei Gruppen ein statistisch signifikanter Unterschied besteht.

Dadurch können wir testen, ob die Lerntechnik einen Einfluss auf die Prüfungsergebnisse hat, sobald der Einfluss der Kovariate entfernt wird.

Wenn wir also feststellen, dass es einen statistisch signifikanten Unterschied in den Prüfungsergebnissen zwischen den drei Lerntechniken gibt, können wir sicher sein, dass dieser Unterschied auch nach Berücksichtigung der aktuellen Note der Schüler in der Klasse besteht (d. h. wenn sie … geht es ihnen bereits gut oder ob es ihnen bereits gut geht). nicht im Unterricht) .

ANCOVA-Annahmen

Vor der Durchführung einer ANCOVA ist es wichtig sicherzustellen, dass die folgenden Annahmen erfüllt sind:

• Die Kovariate(n) und die Faktorvariable(n) sind unabhängig – Die Kovariate und die Faktorvariable müssen unabhängig voneinander sein, da das Hinzufügen eines Kovariatenterms zum Modell nur dann sinnvoll ist, wenn die Kovariate und die Faktorvariable unabhängig voneinander wirken Antwortvariable.
• Die Kovariate(n) sind kontinuierliche Daten. Kovariaten müssen kontinuierlich sein (dh Intervall- oder Verhältnisdaten).
• Homogenität der Varianzen – Die Varianzen zwischen den Gruppen sollten ungefähr gleich sein.
• Unabhängigkeit – Beobachtungen in jeder Gruppe müssen unabhängig sein.
• Normalität – Die Daten sollten in jeder Gruppe ungefähr normalverteilt sein.
• Keine extremen Ausreißer – In keiner der Gruppen sollte es extreme Ausreißer geben, die die ANCOVA-Ergebnisse erheblich beeinflussen könnten.

ANCOVA: Beispiel

Eine Lehrerin möchte wissen, ob sich drei verschiedene Lerntechniken auf die Prüfungsergebnisse auswirken, möchte aber die aktuelle Note berücksichtigen, die der Schüler bereits in der Klasse hat.

Es wird eine ANCOVA unter Verwendung der folgenden Variablen durchgeführt:

• Faktorvariable: technische Studie
• Kovariate: aktuelle Punktzahl
• Antwortvariable: Prüfungsergebnis

Die folgende Tabelle zeigt den Datensatz der 15 Studenten, die für die Teilnahme an der Studie rekrutiert wurden:

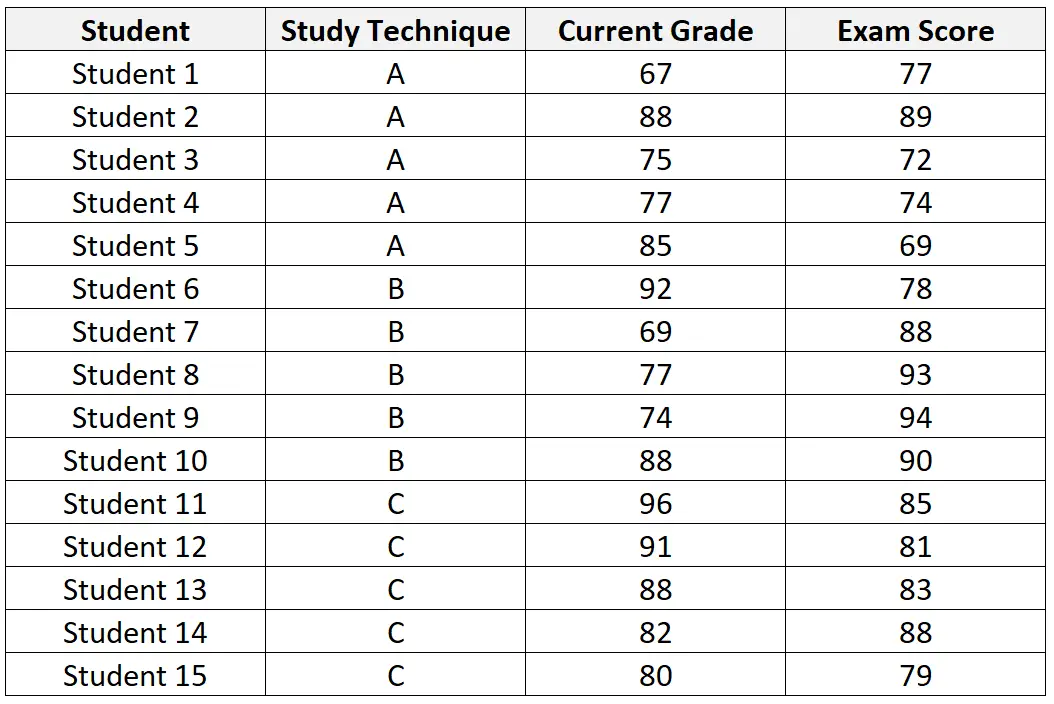
Nach Durchführung einer ANCOVA für den Datensatz erhält der Lehrer die folgenden Ergebnisse:

Der p-Wert für die Studientechnik beträgt 0,03155 . Da dieser Wert kleiner als 0,05 ist, können wir die Nullhypothese ablehnen, dass jede der Lerntechniken zu derselben durchschnittlichen Prüfungsnote führt, selbst wenn die aktuelle Note des Schülers in der Klasse berücksichtigt wird .

Um genau zu bestimmen, welche Lerntechniken zu unterschiedlichen durchschnittlichen Prüfungsergebnissen führen, muss der Lehrernachträgliche Tests durchführen.

Zusätzliche Ressourcen

So führen Sie eine ANCOVA in Excel durch
So führen Sie eine ANCOVA in R durch
So führen Sie eine ANCOVA in Python durch
Die Unterschiede zwischen ANOVA, ANCOVA, MANOVA und MANCOVA