So führen sie eine einfache lineare regression in spss durch

Die einfache lineare Regression ist eine Methode, mit der wir die Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen verstehen können.

In diesem Tutorial wird erläutert, wie Sie eine einfache lineare Regression in SPSS durchführen.

Beispiel: Einfache lineare Regression in SPSS

Nehmen wir an, wir haben den folgenden Datensatz, der die Anzahl der gelernten Stunden und die Prüfungsnote von 20 Studenten zeigt:

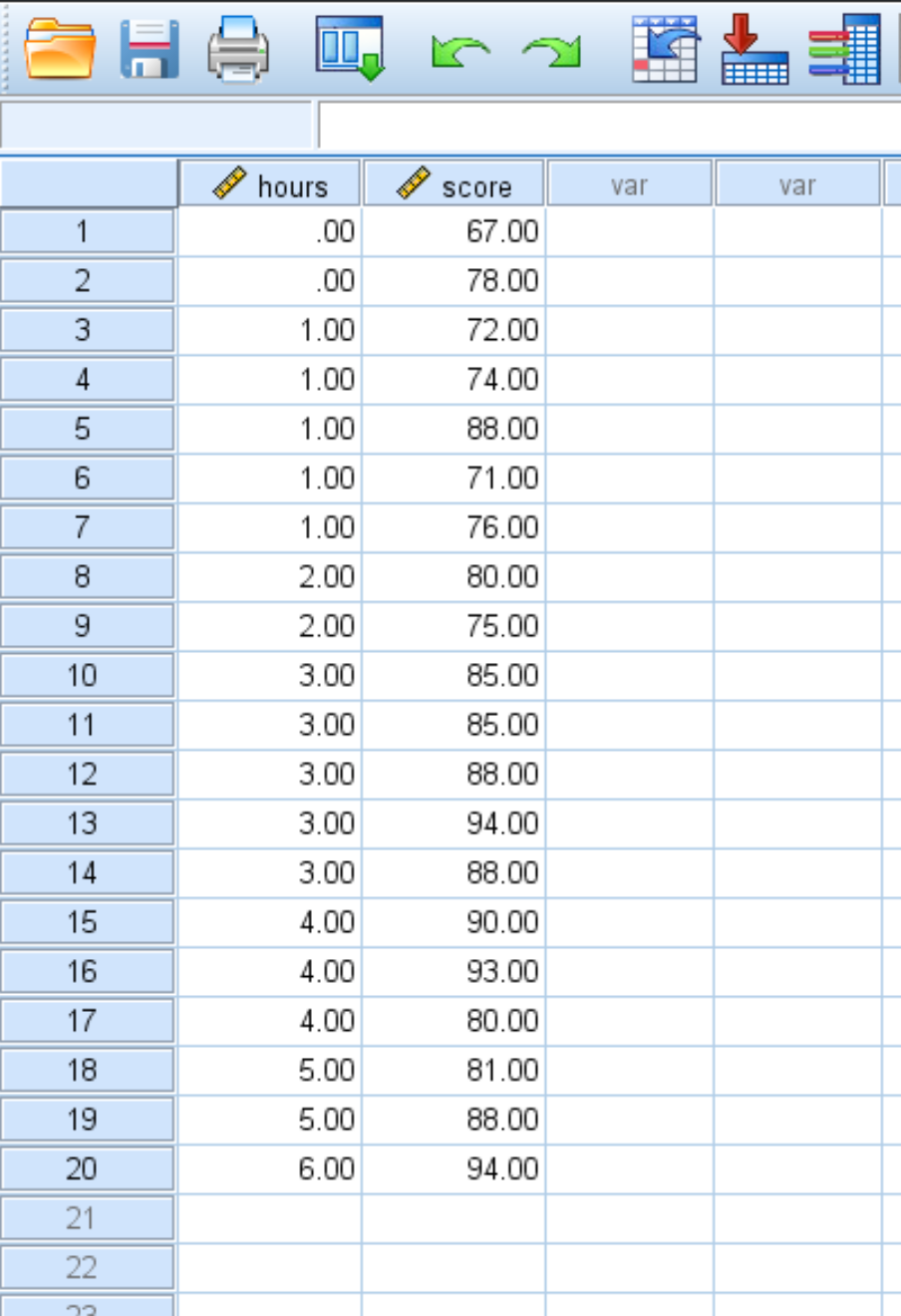
Führen Sie die folgenden Schritte aus, um eine einfache lineare Regression für diesen Datensatz durchzuführen und die Beziehung zwischen den gelernten Stunden und der Prüfungspunktzahl zu quantifizieren:

Schritt 1: Visualisieren Sie die Daten.

Zunächst erstellen wir ein Streudiagramm, um die Beziehung zwischen Stunden und Punktzahl zu visualisieren, um sicherzustellen, dass die Beziehung zwischen den beiden Variablen linear zu sein scheint. Andernfalls wäre die einfache lineare Regression keine geeignete Technik.

Klicken Sie auf die Registerkarte „Diagramme“ und dann auf „Diagrammersteller“ :

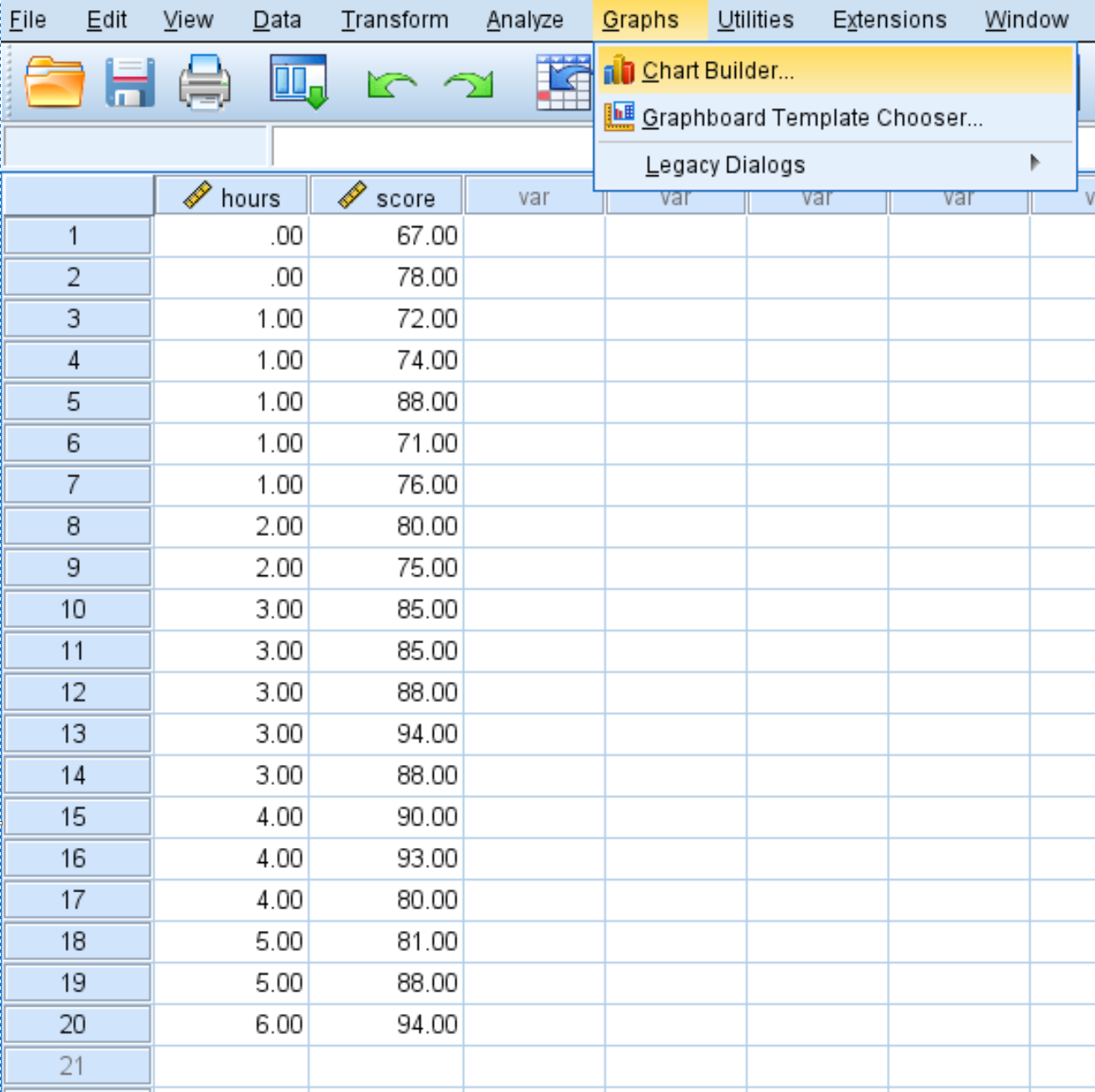
Klicken Sie im Menü „Auswählen aus“ auf „Streuung/Punkt“ und ziehen Sie es in das Hauptbearbeitungsfenster. Ziehen Sie dann die variablen Zeiten auf die x-Achse und den Punktestand auf die y-Achse.

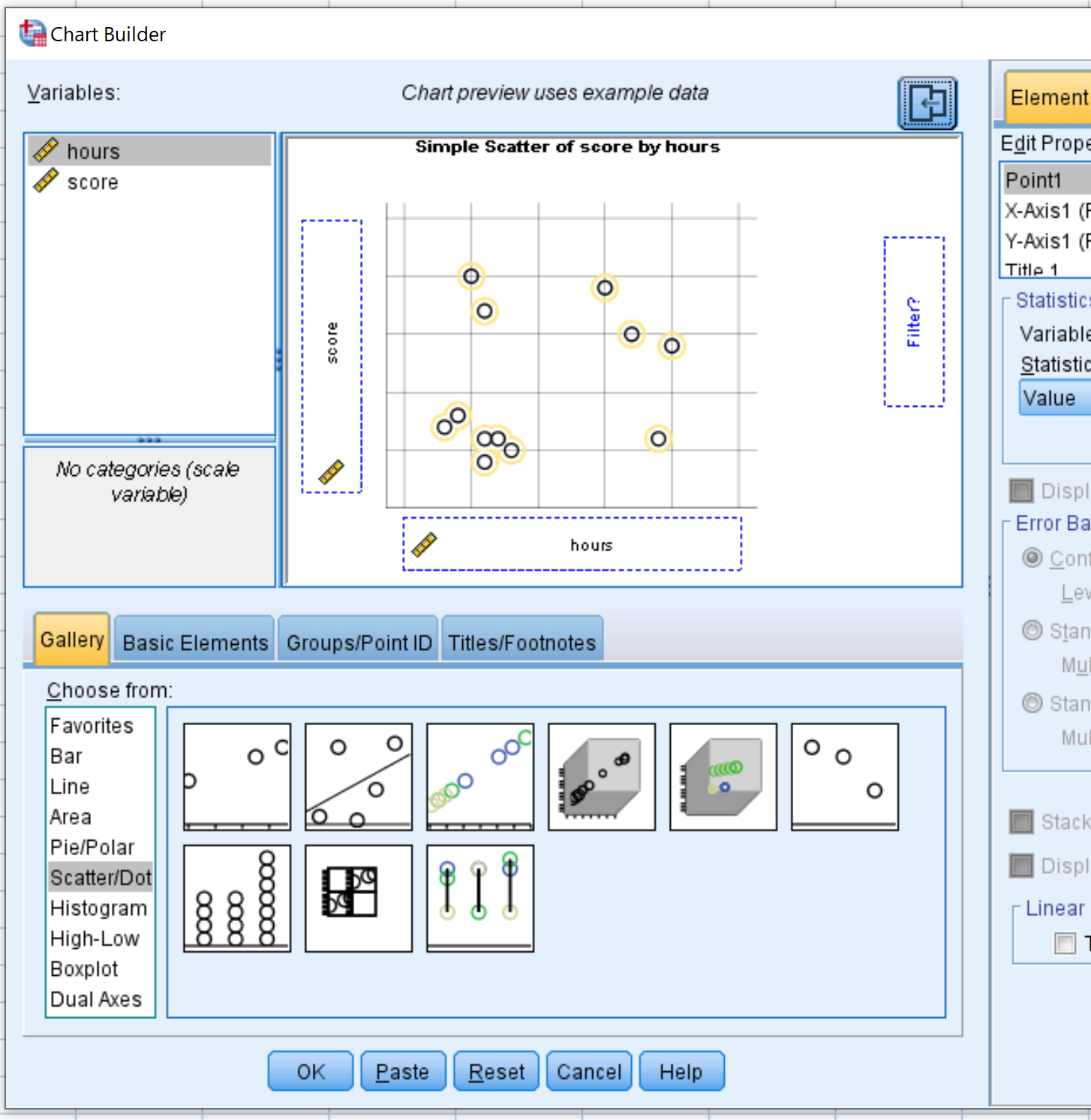
Sobald Sie auf OK klicken, wird das folgende Streudiagramm angezeigt:

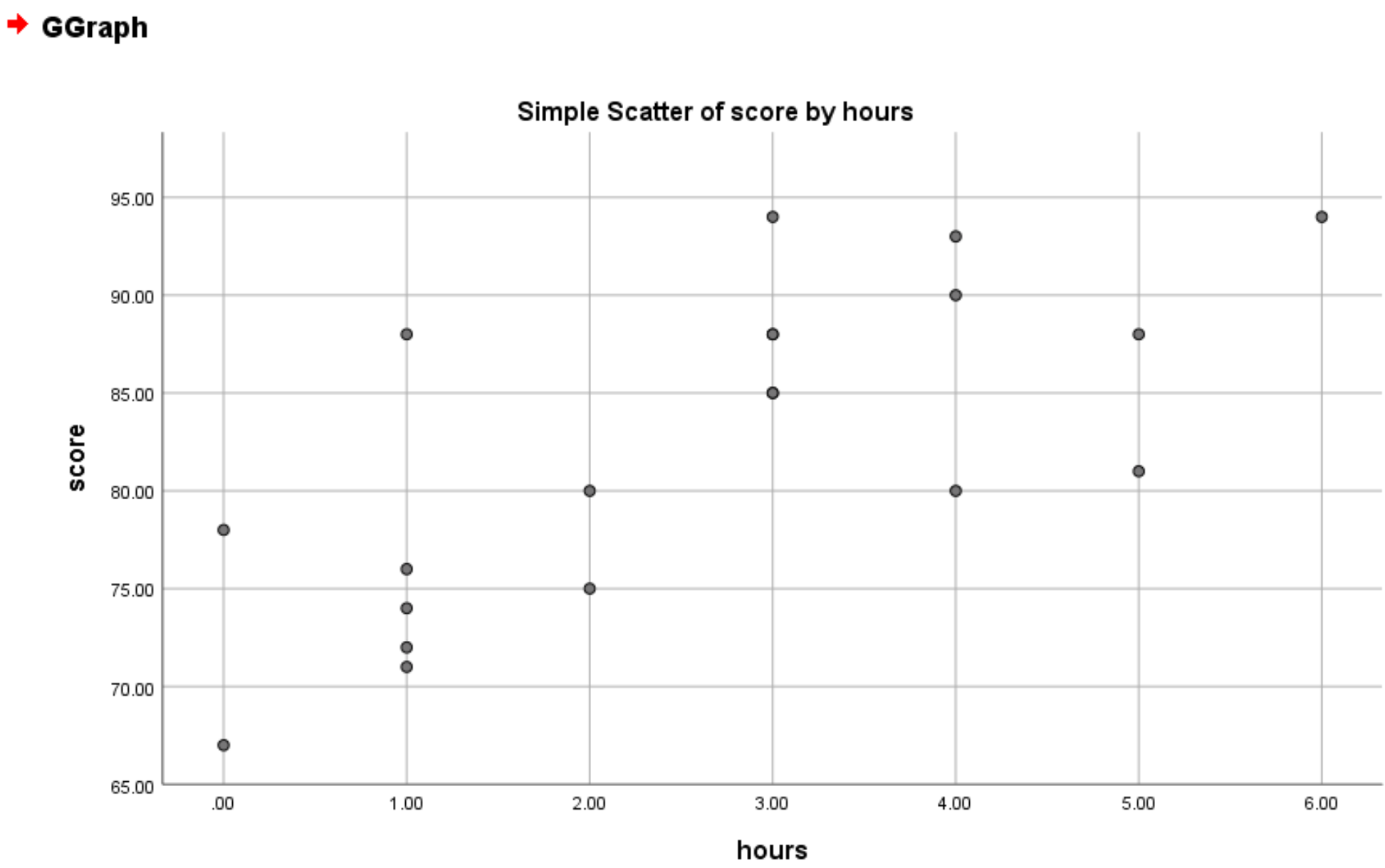
Aus der Grafik können wir ersehen, dass zwischen Stunden und Punktzahl ein positiver linearer Zusammenhang besteht. Im Allgemeinen erzielen Studierende, die mehr Stunden lernen, tendenziell bessere Ergebnisse.

Da zwischen den beiden Variablen eine klare lineare Beziehung besteht, werden wir ein einfaches lineares Regressionsmodell an den Datensatz anpassen.

Schritt 2: Passen Sie ein einfaches lineares Regressionsmodell an.

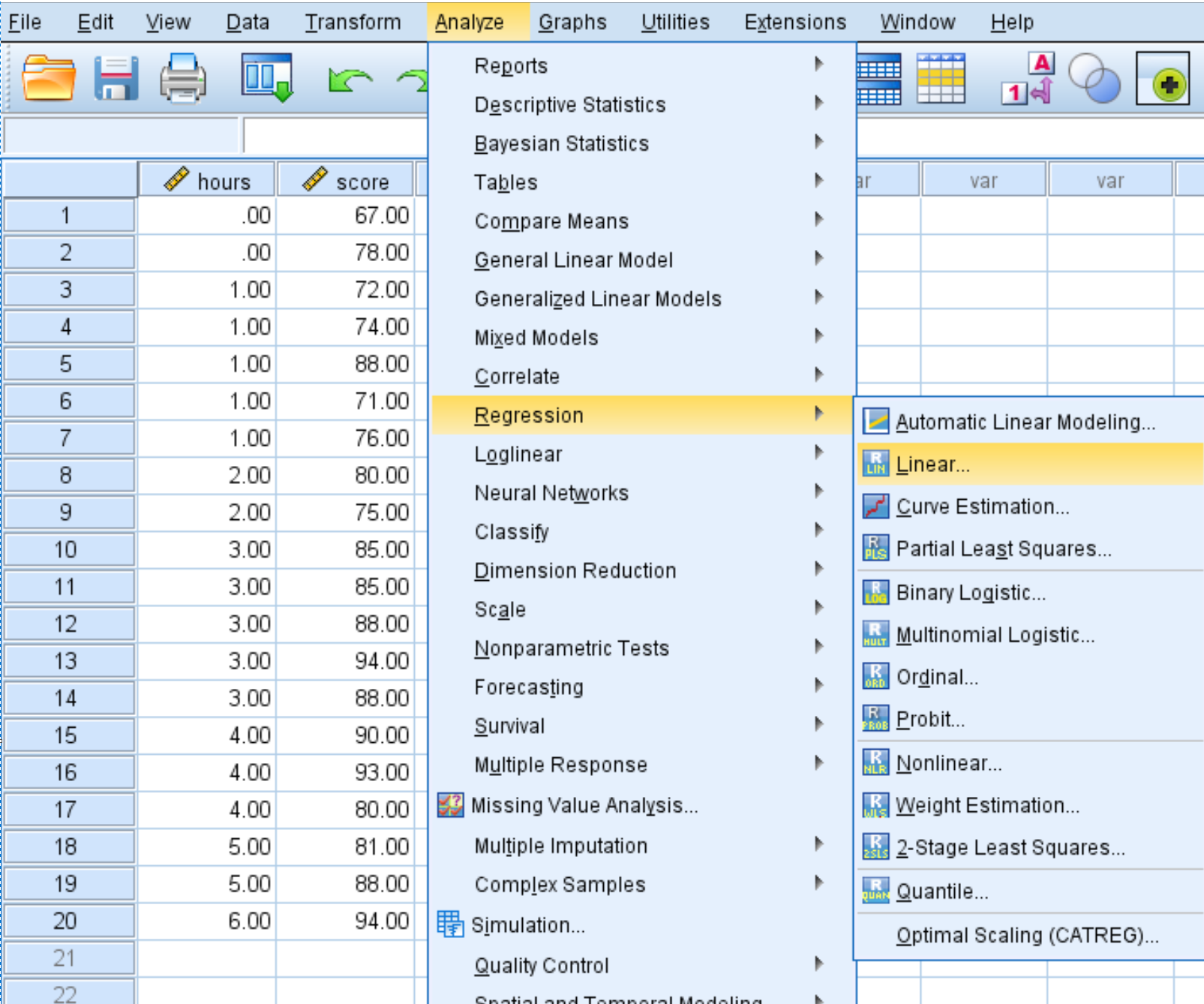
Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Regression“ und dann auf „Linear“ :

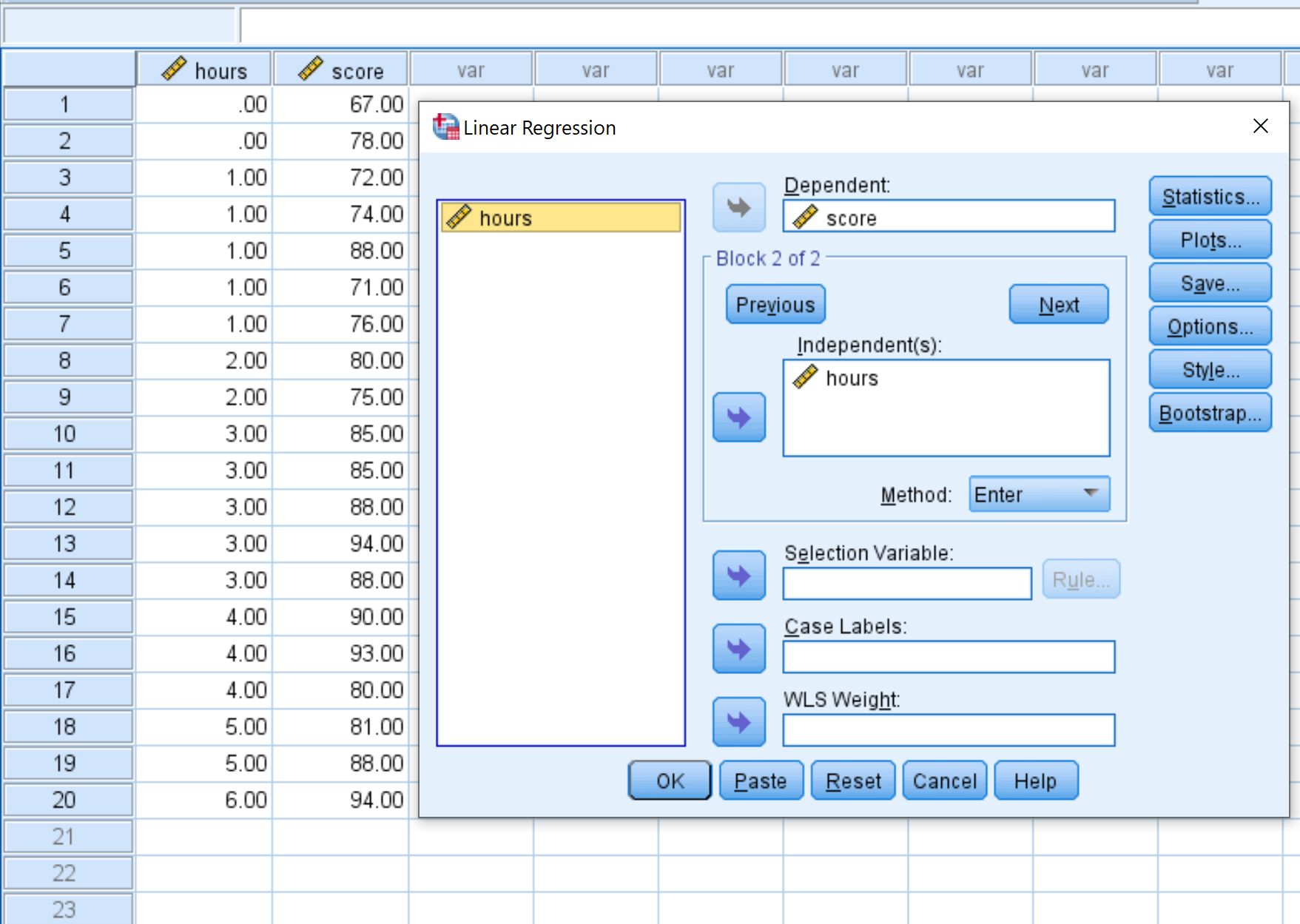
Ziehen Sie im neuen Fenster, das erscheint, die Variable „ Score“ in das Feld „Abhängig“ und die Stunden in das Feld „Unabhängig“. Klicken Sie dann auf OK .

Schritt 3: Interpretieren Sie die Ergebnisse.

Sobald Sie auf OK klicken, werden die Ergebnisse der einfachen linearen Regression angezeigt. Die erste Tabelle, die uns interessiert, ist die mit dem Titel „Modellzusammenfassung“ :

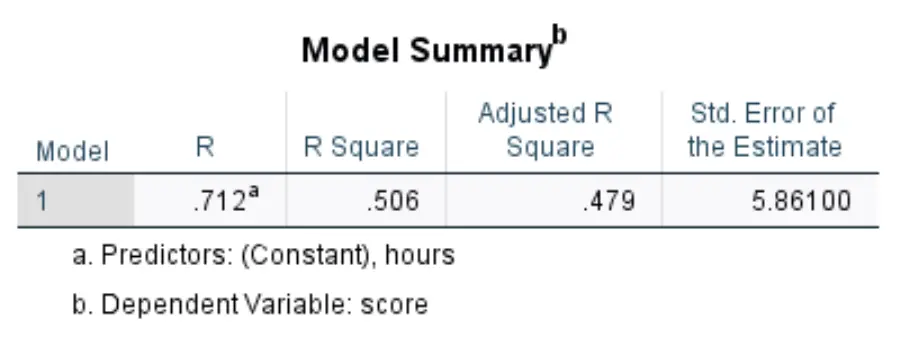
So interpretieren Sie die relevantesten Zahlen in dieser Tabelle:

• R-Quadrat: Dies ist der Anteil der Varianz in der Antwortvariablen, der durch die erklärende Variable erklärt werden kann. In diesem Beispiel können 50,6 % der Abweichungen bei den Prüfungsergebnissen durch die gelernten Stunden erklärt werden.
• Standard. Schätzfehler: Der Standardfehler ist der durchschnittliche Abstand zwischen den beobachteten Werten und der Regressionsgeraden. In diesem Beispiel weichen die beobachteten Werte im Durchschnitt um 5.861 Einheiten von der Regressionsgeraden ab.

Die folgende Tabelle, die uns interessiert, trägt den Titel Koeffizienten :

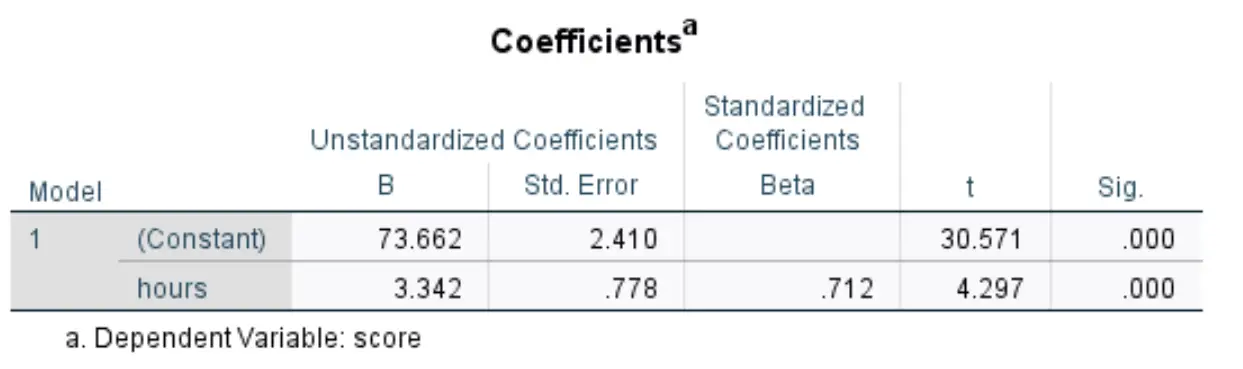
So interpretieren Sie die relevantesten Zahlen in dieser Tabelle:

• Nicht standardisiertes B (Konstante) : Dies gibt uns den Durchschnittswert der Antwortvariablen an, wenn die Prädiktorvariable Null ist. In diesem Beispiel beträgt die durchschnittliche Prüfungspunktzahl 73,662 , wenn die gelernten Stunden null sind.
• B unstandardisiert (Stunden): Dies gibt uns die durchschnittliche Änderung der Antwortvariablen an, die mit einem Anstieg der Prädiktorvariablen um eine Einheit verbunden ist. In diesem Beispiel ist jede zusätzliche gelernte Stunde mit einer durchschnittlichen Steigerung der Prüfungspunktzahl um 3.342 verbunden.
• Sig (Stunden): Dies ist der p-Wert, der der Teststatistik während der Stunden zugeordnet ist. Da dieser Wert in diesem Fall kleiner als 0,05 ist, können wir daraus schließen, dass die Prädiktorvariable Stunden statistisch signifikant ist.

Schließlich können wir mithilfe der Werte von Konstante und Stunden eine Regressionsgleichung bilden. In diesem Fall wäre die Gleichung:

Geschätzte Prüfungspunktzahl = 73,662 + 3,342*(Stunden)

Mit dieser Gleichung können wir die geschätzte Prüfungspunktzahl eines Schülers ermitteln, basierend auf der Anzahl der gelernten Stunden.

Beispielsweise sollte ein Student, der 3 Stunden lernt, eine Prüfungspunktzahl von 83,688 erreichen:

Geschätztes Prüfungsergebnis = 73,662 + 3,342*(3) = 83,688

Schritt 4: Melden Sie die Ergebnisse.

Abschließend wollen wir die Ergebnisse unserer einfachen linearen Regression zusammenfassen. Hier ist ein Beispiel dafür:

Zur Quantifizierung des Zusammenhangs zwischen Lernstunden und Prüfungsnote wurde eine einfache lineare Regression durchgeführt. Für die Analyse wurde eine Stichprobe von 20 Studierenden herangezogen.

Die Ergebnisse zeigten, dass ein statistisch signifikanter Zusammenhang zwischen den gelernten Stunden und der Prüfungsnote bestand (t = 4,297, p < 0,000) und dass die gelernten Stunden 50,6 % der erklärten Variabilität der Prüfungsnote ausmachten. die Prüfung.

Es stellte sich heraus, dass die Regressionsgleichung lautete:

Geschätzte Prüfungspunktzahl = 73,662 + 3,342*(Stunden)

Jede zusätzliche gelernte Stunde ist mit einer durchschnittlichen Verbesserung der Prüfungspunktzahl um 3.342 verbunden.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SPSS ausführen:

So führen Sie eine multiple lineare Regression in SPSS durch
So führen Sie eine quadratische Regression in SPSS durch
So führen Sie eine logistische Regression in SPSS durch